Fərqsizlik Əyriləri Əsla Bir-Birini Kəsməzlər
İqtisadi insanın xüsusiyyətlərindən olan `tutarlı olma` xüsusiyyətiylə, fərqsizlik əyrilərinin bir və ikinci xüsusiyyətlərini birlikdə düşünsək, fərqsizlik əyrilərinin üçüncü xüsusiyyəti ortaya çıxar. Bu xüsusiyyəti şəkil köməyi ilə asanlıqla izah edə bilərik. Fərz edək ki, i hər hansı fərqsizlik əyrisi, k isə i əyrisini kəsə biləcəyini iddia etdiyimiz başqa bir əyri olsun. Kəsişmə nöqtəsinə A desək, A nöqtəsi hər iki əyridə də olduğu üçün bu əyrilərin hər ikisi də eyni ümumi faydalılığa malik əmtəə bölgülərini təmsil edir deməkdir.
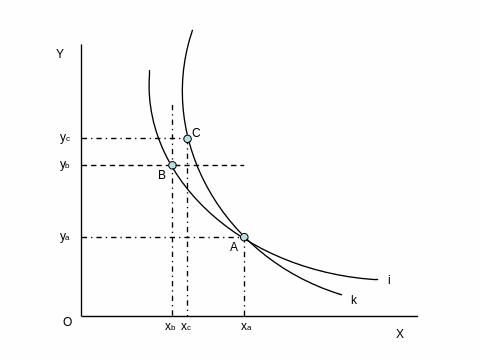
Halbuki, i üzərindəki B nöqtəsinin, k üzərindəki C nöqtəsinə görə daha az ümumi faydalılığı təmsil etdiyi aydındır. Çünki,
yc > yb
xc > xb
dir və istehlakçı C nöqtəsində B nöqtəsinə görə hər iki əmtəədan də daha çox istehlak edir. Belə olan halda, i fərqsizlik əyrisidirsə, k deyil (ya da tam tərsi). Beləliklə, iki fərqsizlik əyrisinin bir-birini kəsməyəcəyi isbat edilmiş oldu.
Fərqsizlik Əyrilərinin Mənfi Meylilik Göstərmələri
Bir əmtəənin digərinin əvəzinə istifadə edilməsinə əvəzləmə deyilir. Başqa bir deyişlə, əvəzləmə olan halda, bir əmtəənin istehlakı azaldılarkən, digərinin istehlakı artırılır və tələbat daha çox bu yeni əmtəə ilə aradan qaldırılmağa çalışılır deməkdir. Fərqsizlik əyrisi üzərində hərəkət edərsək, davamlı bir əvəzləmənin olduğunun şahidi olarıq. Çünki istehlakçı özünün ümumi faydalılığını sabit tuta bilmək üçün bir əmtəənn istehlak miqdarını artırarsa mütləq digərinin istehlakını azaltmalıdır ki, onun ümumi faydası artmasın. Bu səbəbdən, fərqsizlik əyriləri mənfi meylli, yəni azalan meylliliyi olan əyrilərdir. Məsələn, bir fərqsizlik əyrisində sol yuxarıdan sağ aşağıya doğru edərsək X əmtəəsində istehlak miqdarı artarkən, Y əmtəəsində istehlak miqdarı azalır.
Azalan Son Hədd (Marjinal) Əvəzləmə Nisbəti və Fərqsizlik Əyrilərinin “Sıfır” Nöqtəsinə Görə Xaricə Kənar Olması
Bir fərqsizlik əyrisi üzərindəki bir nöqtə (məsələn A nöqtəsi) ətrafında, X əmtəəsində istehlak miqdarındakı dəyişikliyin Y əmtəəsinin istehlak miqdarında yaratdığı təsirə, son hədd (marjinal) əvəzləmə nisbəti adı verilir və bu nisbət bu nöqtə üçün təyin olunur.
Başqa bir ifadəylə son hədd (marjinal) əvəzləmə nisbəti, fərqsizlik əyrisi üzərində bir nöqtə ətrafında istehlakçının bir əmtəəni digərinə tərcih etdiyi dəyişmə nisbətini göstərir.
Şəkildə A və A1 ümumi faydalılıq nöqtələrində Y əmtəəsinin əvəzləmə miqdarındakı dəyişiklik (ya) B və B1 ümumi faydalılıq nöqtələrindəki Y əmtəəsinin əvəzləmə miqdarındakı dəyişiklikdən (yb) daha böyük olduğu görülür. Yəni eyni ümumi faydalılığı qoruya bilmək üçün A nöqtəsindən B nöqtəsinə keçən vaxt Y əmtəəsinin əvəzləmə miqdarındakı dəyişiklik (nisbət) azalmaqdadır. Azalan son hədd (marjinal) əvəzləmə nisbəti məhz bu vəziyyət izah edir.
Büdcə Məhdudiyyəti və Büdcə Xətti
İstehlakçının əmtəələri əldə etmək üçün malik olduğu gəlirlərin və ya borc alma imkanlarının məhdud olması onun istehlak xərclərini də məhdudlaşdırır. Belə olan halda, xərc imkanlarının pulla ifadəsinə büdcə məhdudiyyəti adı verilir.
X əmtəəsinin qiymətini Px, istehlakçının büdcəsini M ilə göstərsək, bu büdcə ilə satın alına biləcək X əmtəəsinin maksimum miqdarı
olacaq.
Məsələn, almanın qiymətinin 1 AZN/kg isə istehlakçı 10 AZN ilə 10 kq alma ala biləcək. İstehlakçının yalnız alma deyil armud da istehlak etdiyini və armudun qiymətinin isə 2 AZN olduğunu düşünsək, istehlakçı eyni büdcə ilə hər iki əmtəədan almaq istərsə əmtəə bölgüsü, məsələn 5 kq alma, 2.5 kq armud şəklində olacaq.
Yenə yuxarıdakı örnəklə davam etsək, büdcəyə M, almanın qiymətinə Px, armudun qiymətinə Py, alma və armudun miqdarlarına da x və y desək, istehlakçı büdcəsinin tamamının xərclənməsi halında,
M = Px*x + Py*y
yaza bilərik. Bu ifadə isə büdcə məhdudiyyətinin riyazi ifadəsidir.
Bu düsturdan istifadə edərək, aşağıdakı nəticələri əldə etmək mümkündür:
y = M/Py - (Px/Py)*x
Nümunədəki rəqəmlərdən istifadə etsək:
y = 5 - 0.5x
kimi bir funksiya əldə edilir.
Burada,
x = 0 üçün y = 5
y = 0 üçün x = 10
olduğu və iki nöqtədən yalnız bir düz xətt keçdiyi üçün bu funksiyanı şəkildəki kimi çəkə bilərik:
Büdcə Xətti
Bu xətt üzərindəki hər nöqtə (B kimi) büdcədəki vəsaitin hamısının xərcləndiyini, B"in altındakı hər nöqtə (A kimi), daha xərclənə biləcək vəsaitin olduğunu, düz xəttin sağ yuxarı tərəfindəki hər nöqtə (C kimi) isə , istehlakçının bu əmtəə bölgüsündə satılan əmtəələri almaq üçün vəsaitinin yetərsiz olduğunu göstərər.
Büdcə Xəttinin Meylliliği
Bilindiyi kimi bir düz xəttin hərəkət trayektoriyasını müəyyənləşdirmək üçün bu düz xətt tənliyində müstəqil dəyişənin əmsalından istifadə olunur. Yəni,
Y = a + bx
tənliyində b trayektoriyanı göstəir. Bu qaydanı büdcə düz xəttinə tətbiq etsək, müstəqil dəyişən olaraq qəbul etdiyimiz x-in əmsalı olan (-) büdcə düz xəttinin trayektoriyası olacaq.
Təkrar nümunəyə qayıtsaq, əvvəlcə tapdığımız kimi
-Px/Py = -1/2 = -0.5
olacaq.
Əmsal dəyərinin (-) olması müəyyən bir büdcənin alma-armud bölgüsü ilə hamısı xərclənərsə, fərdin məsələn bir az daha alma satın ala bilməsi üçün mütləq bir miqdar armud almaqdan imtina etməsinin lazım olduğunu göstərər. Bir vahid çox alma almaq üçün nə qədər armud almaqdan imtina etməsini isə Px/Py nisbəti göstərər ki, bu da 0.5-dir.