Вопрос 3. Обратная матрица.

Если определитель квадратной матрицы отличен от нуля, то матрица называется невырожденной. Если же определитель матрицы равен нулю, то матрица называется вырожденной.

Если – квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая и удовлетворяющая условию

.

Теорема: для того, чтобы квадратная матрица имела обратную, необходимо и достаточно, чтобы матрица была невырожденной, то есть чтобы .

Матрица , обратная получается следующим образом:

1. Составим матрицу , заменяя в матрице каждый элемент его алгебраическим дополнением , деленным на определитель матрицы :

.

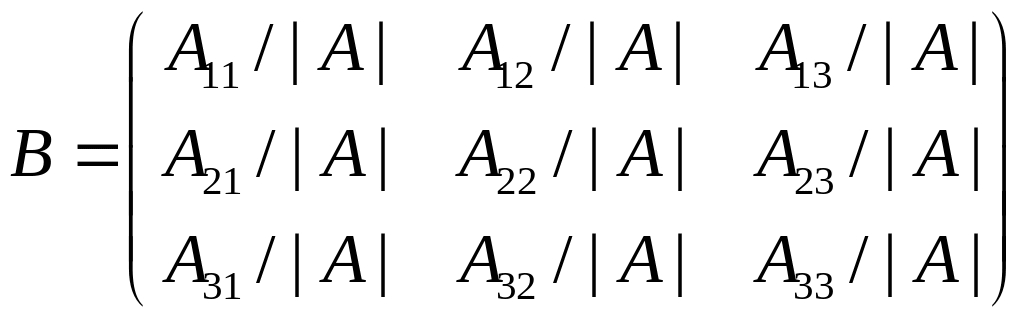2. Составим матрицу , как транспонированную к :

.

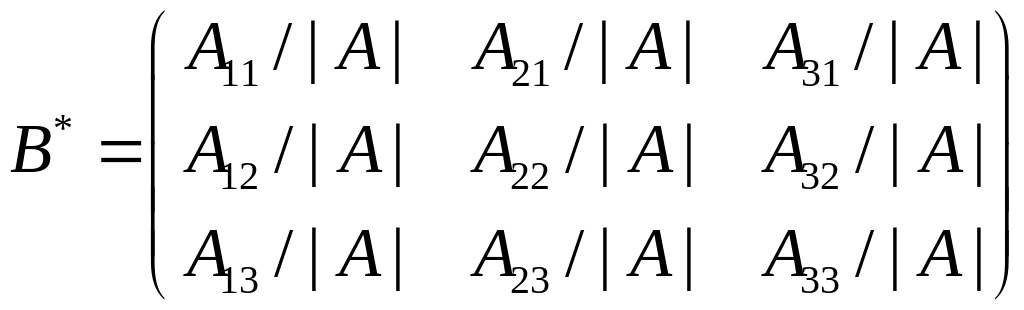является обратной .

Пример 15:

;

;

; ; ; ; ; ; ; ; .

,

.

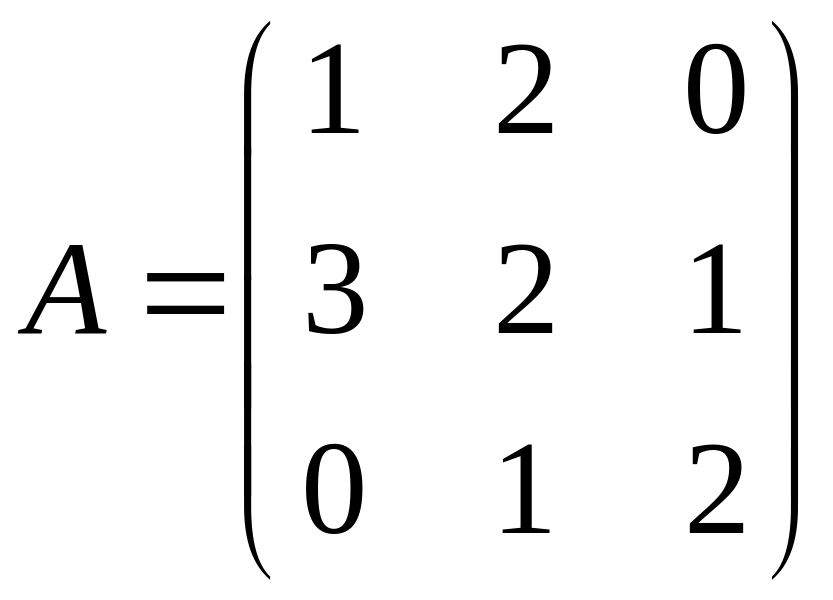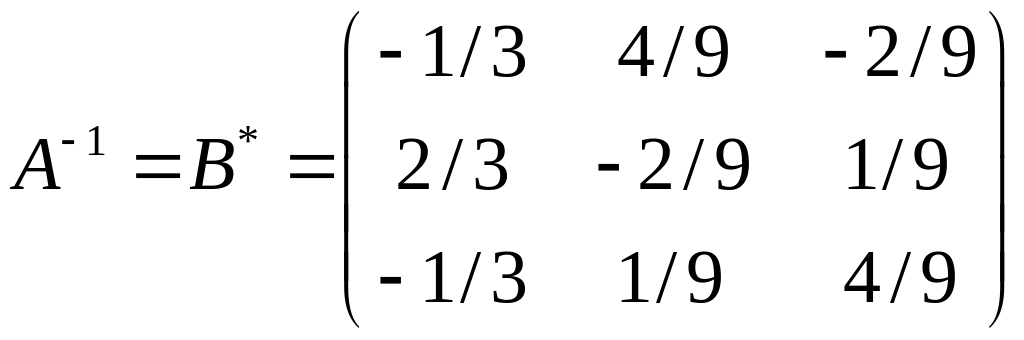Определители матриц и обратны по величине.

.

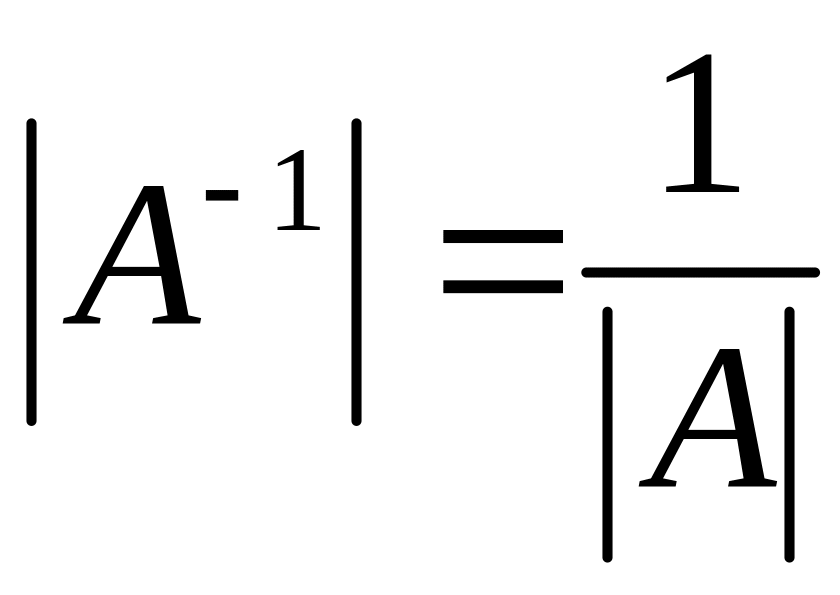Знаем, что .

Вопрос 4. Ранг матрицы. Эквивалентные матрицы. Основные методы нахождения ранга матрицы.

Рассмотрим прямоугольную матрицу размера , то есть имеющую строк и столбцов. Выделим в ней произвольные строк и столбцов. Элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу порядка .

Минором -го порядка матрицы называется определитель квадратной матрицы, получаемой из данной выделением произвольных строк и столбцов.

Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров. Если ранг матрицы равен , то это означает, что в матрице есть хотя бы один отличный от нуля минор порядка , но всякий минор порядка, больше чем , равен нулю. Ранг матрицы обозначают или .

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Если ранг матрицы равен рангу матрицы , то есть , то матрицы называют эквивалентными и записывают .

Основные методы нахождения ранга матрицы.

1. Метод единиц и нулей. С помощью элементарных преобразований любую матрицу можно привести к виду, когда каждый ее ряд будет состоять только из нулей или из нулей и одной единицы. Тогда число оставшихся единиц и определит ранг исходной матрицы, так как полученная матрица будет эквивалентна исходной.

2. Метод окаймляющих миноров. Минор М_k+1 порядка k + 1, содержащий в себе минор M_k, порядка k, называется окаймляющим минором M_k. Если у матрицы А существует минор M_k ≠ 0, а все окаймляющие его миноры M_k+1= 0, то rang A = k.

Вопрос 5. Элементарные преобразования матрицы.

К элементарным относятся следующие преобразования:

1. умножение всех элементов строки (столбца) на число ,

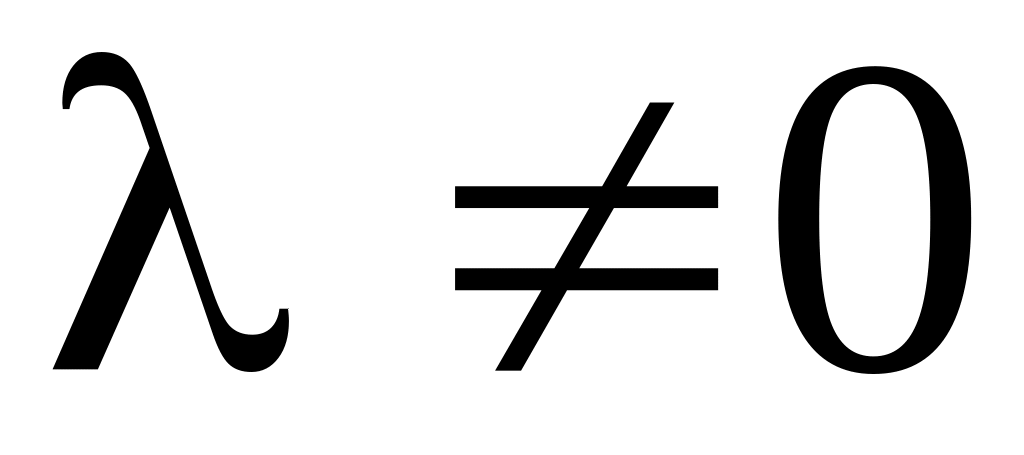2. прибавление к элементам одной строки элементов другой строки, умноженных на одно и то же число (то же верно для столбца),

3. перемена местами строк (столбцов),

4. отбрасывание нулевых строк (столбцов).

После элементарных преобразований ранг матрицы не меняется, то есть матрицы, получаемые после элементарных преобразований, эквивалентны.