Элементы линейной алгебры. Тема. Матрицы и определители.

Вопрос 1. Матрицы, основные понятия, действия над матрицами.

Матрицами называют математические объекты, имеющие вид таблицы с размерами , где - число строк, а - число столбцов.

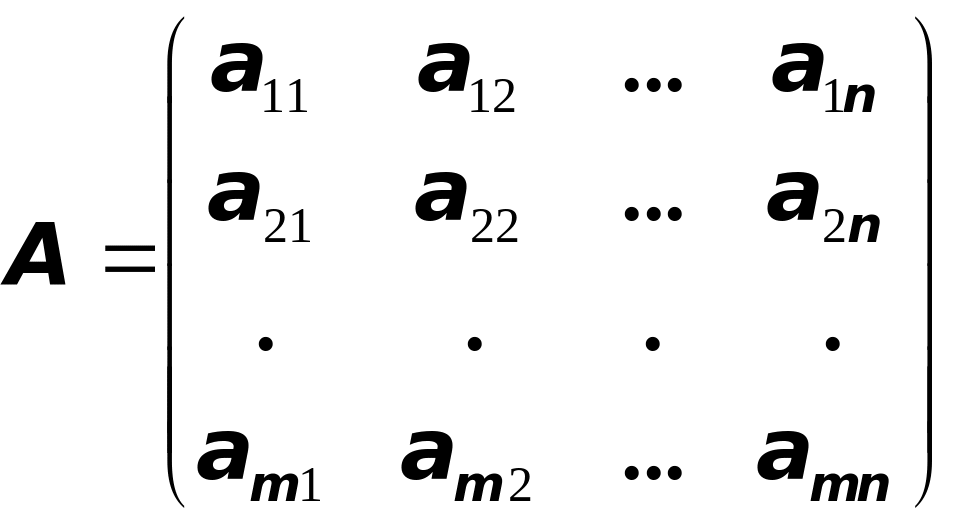
Элементами матрицы могут быть как числа действительные или комплексные, так и другие математические объекты, например, функции (в этом случае матрица называется функциональной).

Иногда матрицы обозначают:

, или ,

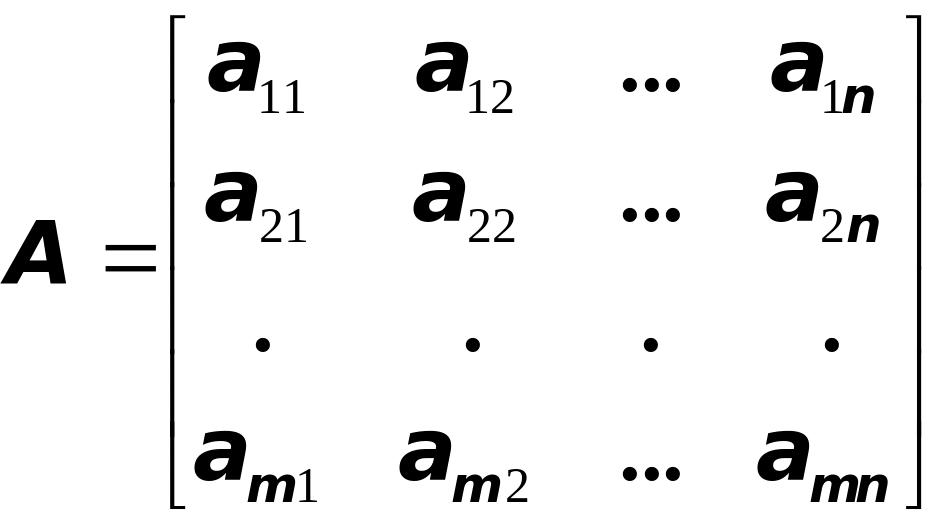или более кратко:

, или , или , .

Если число строк данной матрицы совпадает с числом её столбцов, то матрица называется квадратной, говорят, что она имеет порядок или размеры , т.е. квадратная матрица имеет вид

.

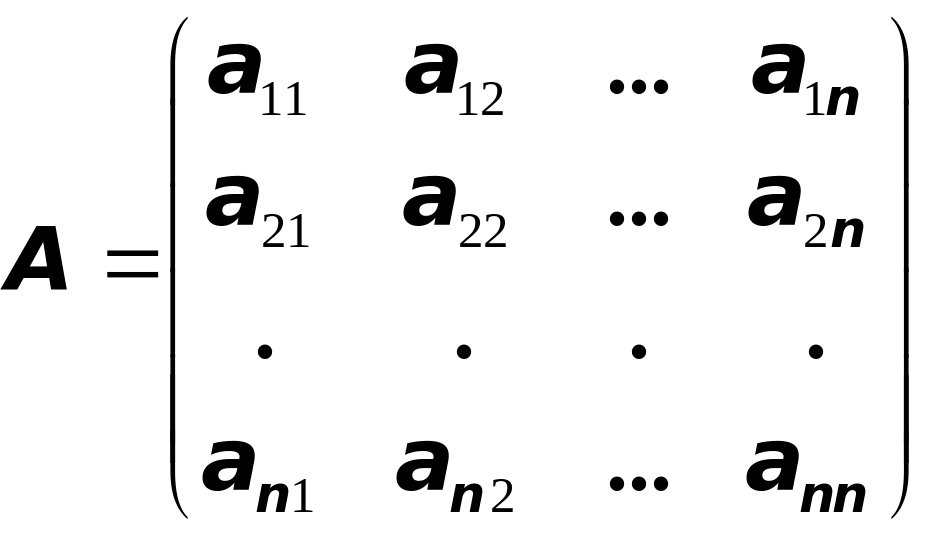Элементы , , …, квадратной матрицы образуют главную диагональ, элементы , , …, образуют побочную диагональ квадратной матрицы, они идут из левого нижнего в правый верхний угол матрицы.

Рассмотрим таблицу вида: .

Числа с двумя индексами , , , называются элементами матрицы. Первый индекс означает номер строки, второй – номер столбца, на пересечении которых стоит данный элемент.

Симметрической матрицей называется квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, равны друг другу, то есть .

Пример 1:

Диагональной матрицей называется квадратная матрица, у которой все элементы, не находящиеся на главной диагонали, равны нулю.

Пример 2: .

Треугольной называется квадратная матрица, если из следует .

Мономиальной называется квадратная матрица, в каждой строке и в каждом столбце которой стоит лишь один элемент, отличный от нуля.

Единичной называется диагональная матрица, у которой каждый элемент, находящийся на главной диагонали, равен единице.

Пример 3: .

Нулевой матрицей называется матрица, у которой все элементы равны нулю и обозначают или .

Следом квадратной матрицы называется сумма ее диагональных элементов.

Матрицы могут быть и прямоугольными, имеющими строк и столбцов, например, .

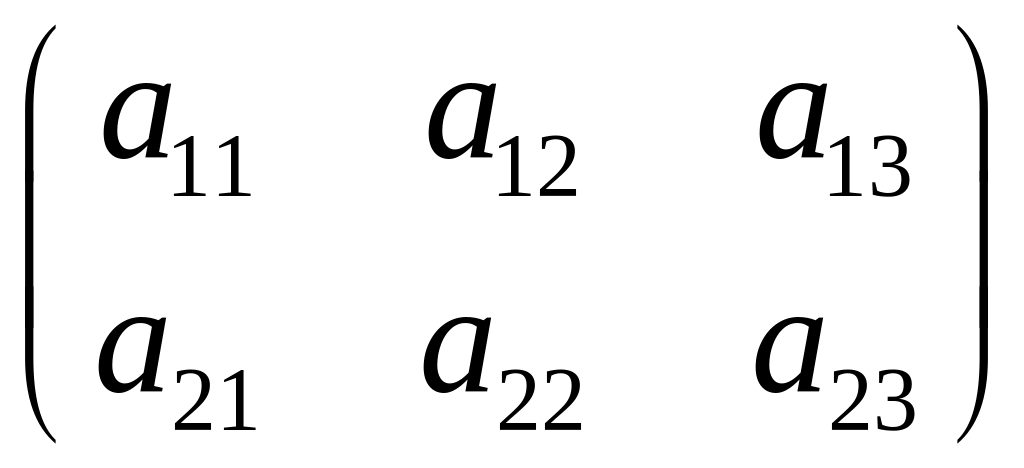Матрица, имеющая только одну строку, называется матрицей-строкой, например, , а матрица, имеющая только один столбец, называют матрицей-столбцом, например: .

Матрицы и называются равными, если они имеют одно и то же число строк и одно и то же число столбцов (то есть, если они одного размера) и если при этом каждый элемент матрицы равен соответствующему элементу матрицы .

;

.

Действия над матрицами.

1. Сумма и разность матриц.

Суммой матриц и , имеющих одинаковое число строк и столбцов

; ,

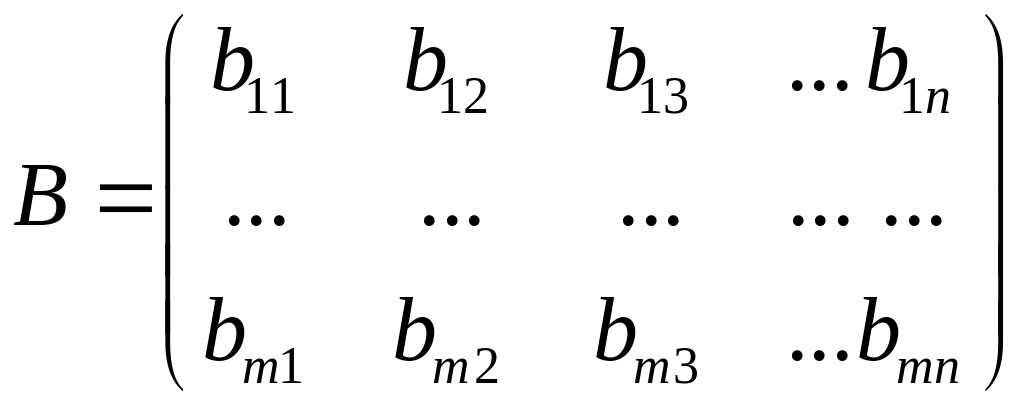называется третья матрица

,

каждый элемент которой равен сумме соответствующих элементов слагаемых матриц, то есть .

Сумма матриц обозначается так .

Аналогично определяется разность матриц: , где .

Пример 4: ; ; , где .

2. Произведение числа на матрицу.

Произведение числа на матрицу называется матрица, определяемая равенством: и получаемая из умножением всех ее элементов на . Обозначается .

3. Умножение матриц.

Пусть заданы две матрицы и , причем число столбцов первой из них равно числу строк второй. Если

, ,

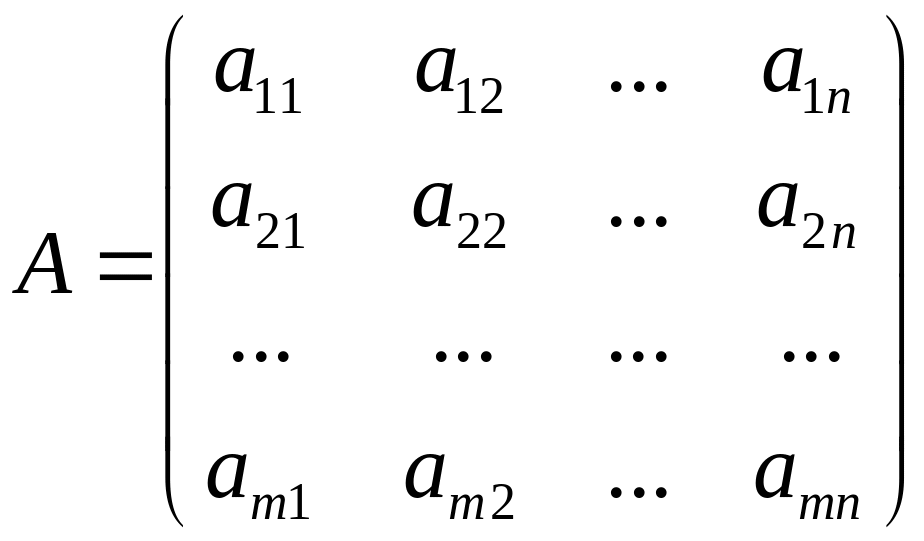то матрица

,

где 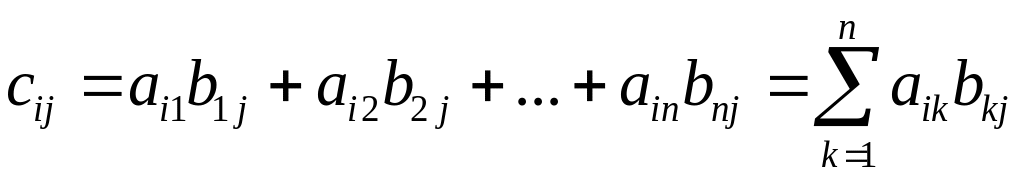называется произведением матрицы на и обозначается .

Правило умножения матриц можно сформулировать так: чтобы получить элемент, стоящий в -ой строке и -ом столбце произведения двух матриц, нужно элементы -ой строки первой матрицы умножить на соответственные элементы -го столбца второй и полученные произведения сложить. В результате умножения получается матрица, имеющая столько строк, сколько у матрицы множимого и столько столбцов, сколько у матрицы множителя.

Пример 5:

Найти произведение матриц ; .

.

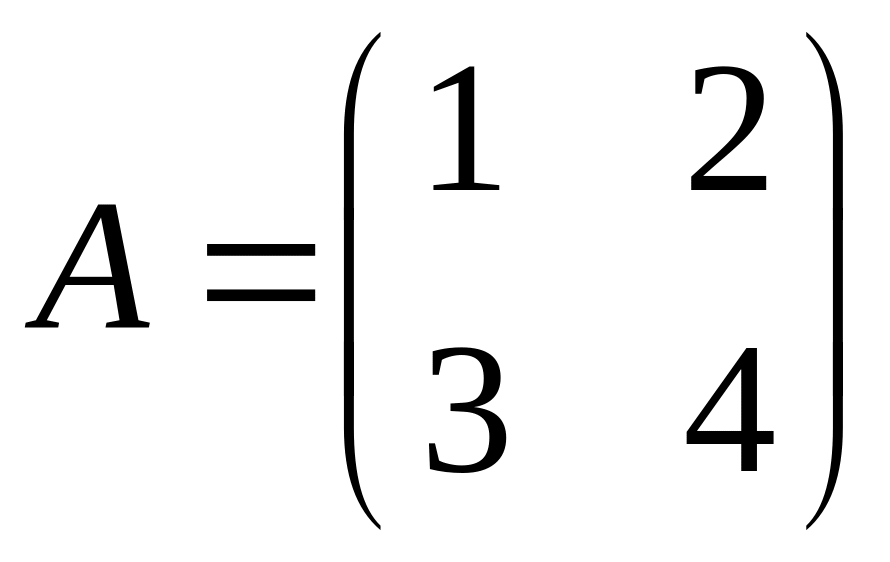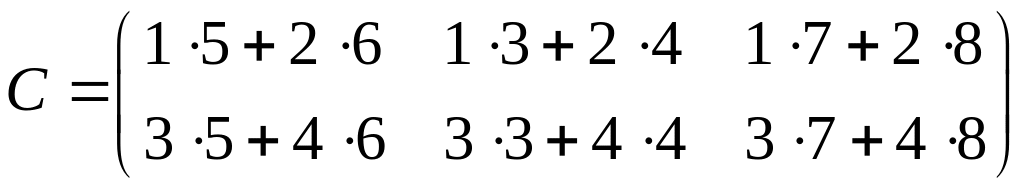Пример 6:

Найти произведение матриц А = и В = .

АВ =  = .

ВА =  = 21 + 44 + 13 = 2 + 16 + 3 = 21.

Пример 7: Найти произведение матриц А= , В =

АВ =  = = .

Замечание 1. Из определения произведения матрицы на матрицу следует, что умножать матрицу на матрицу можно лишь в том случае, если число столбцов матрицы совпадает с числом строк матрицы .

Замечание 2. , так как если , то не определено, т.е. произведение матриц некоммутативно. Квадратные матрицы одного порядка называются коммутирующими, если .

Замечание 3. Очевидно, что , т.е. единичная матрица при умножении матриц играет роль обычной единицы.

Произведение матриц зависит от порядка сомножителей. Причем, если рассматривать матрицы не квадратные, то может случиться даже, что произведение двух матриц в одном порядке будет иметь смысл, а в обратном – нет.

Но, даже для квадратных матриц произведение матриц некоммутативно, то есть не подчиняется переместительному закону.

Пример 8: ,

,

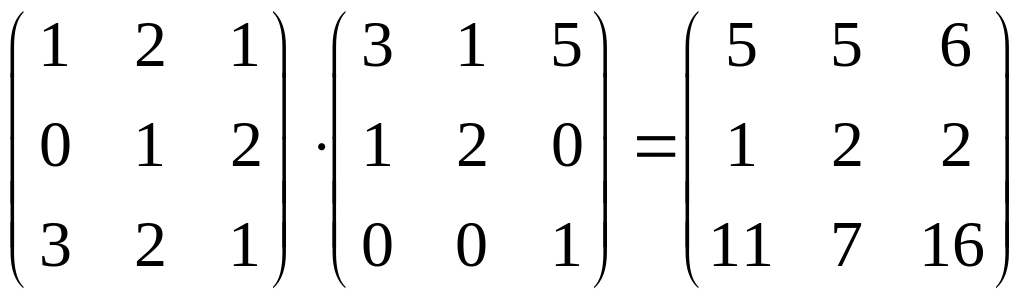очевидно, что .

Если же , то матрицы и называются коммутирующими друг с другом.

Пример 9:

, .

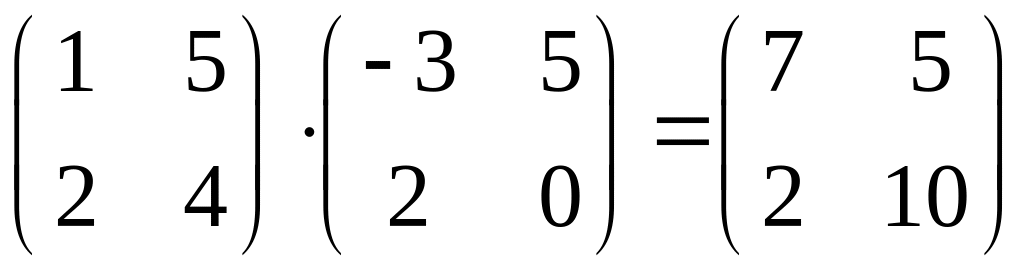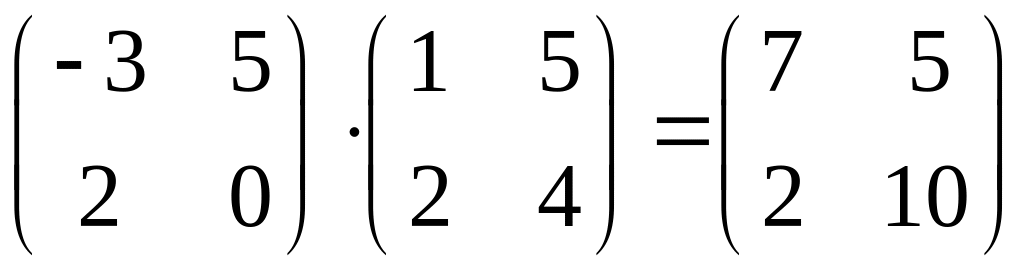Единичная матрица коммутативна с любой матрицей: .

4. Транспонирование матрицы.

Матрица называется транспонированной по отношению к данной матрице , если она получается из матрицы путём замены в ней всех строк на соответствующие им столбцы.

Пусть

=>

Свойства операции транспонирования:

1. ;

2. ;

3. ;

4. .

Матрица , для которой выполняется условие , называется симметрической.

5. Возведение в степень.

Целой положительной степенью А^m (m > 1) квадратной матрицы А называется произведение m матриц, равных А.

Замечание 1. Операция возведения в степень определяется только для квадратных матриц.

Замечание 2. По определению полагают A⁰ = E, A¹ = A. Нетрудно показать, что A^mA^k = A^m+k, (A^m)^k = A^mk.