Контрольні питання

1. Навести перетворення «зірка»–«трикутник» для резистивних елементів.

2. Навести взаємне перетворення реального джерела напруги на реальне джерело струму.

3. Як об’єднати декілька джерел напруги до одного еквівалентного?

4. Як об’єднати декілька джерел струму до одного еквівалентного?

5. Як перенести ідеальне джерело напруги за вузол електричної схеми?

6. Як внести ідеальне джерело струму до контуру?

7. Навести властивості послідовного з’єднання пасивних елементів.

8. Навести властивості паралельного з’єднання пасивних елементів.

Література: [1–4].

Розрахунково-графічне завдання № 2 Тема. Графи електричних кіл. Метод законів Кірхгофа

Мета: розрахунок складних електричних кіл за допомогою методу законів Кірхгофа.

Короткі теоретичні відомості

Розглянемо на прикладі складання системи рівнянь методом законів Кірхгофа (МЗК).

Проаналізуємо схему, зображену на рис 2.1, а. Довільно позначимо напрямки струмів у гілках кола. Будемо вважати, що струми та напруги пасивних елементів узгоджені, тобто збігаються за напрямком.

Кількість вузлів n_В = 5, кількість гілок n_Г = 8 (будемо вважати, що номери гілок збігаються з номерами струмів), кількість джерел струму n_ДС = 1. Побудуємо дерево графа (рис. 2.1, б). З’єднаємо всі вузли за допомогою існуючих гілок таким чином, щоб вони не утворювали замкнутих контурів. Такі гілки називаються ребрами і їх кількість визначається за формулою:

n_Р = n_В – 1,

тобто n_Р = 5 – 1 = 4. Ребрами не можуть бути гілки з джерелами струму, а для нашого прикладу це гілка зі струмом i₇.

а)

б)

Рисунок 2.1 – Електрична схема (а) та її дерево графа (б)

З можливих комбінацій виберемо ребрами гілки, що на рисунку зображені суцільними лініями. Усі останні гілки називають хордами (позначені пунктирними лініями) і їх кількість:

n_Х = n_Г – n_Р = n_Г – (n_В – 1),

тобто n_Х = 8 – (5 – 1) = 4.

Запишемо систему рівнянь за МРК.

За законом струмів Кіргхофа (ЗСК) кількість рівнянь: n_ЗТК = n_В – 1 = 4.

Один з вузлів схеми беруть за базисний і для нього рівняння не записують. У нашому випадку візьмемо за базисний вузол 5.

Рисунок 2.2 – Електрична схема з нанесеними контурами

Запишемо рівняння відповідно до рис. 2.2:

– для вузла 1: –i₁ + i₂ – i₆ = 0;

– для вузла 2: –i₂ + i₃ – i₇ = 0.

– для вузла 3: –i₃ – i₄ + i₈ = 0.

– для вузла 4: i₁ + i₄ + i₅ = 0.

Замінимо струми ємностей через відповідні напруги. У нашому випадку:

. Тоді:

Рівняння за законом напруг Кіргхофа (ЗНК) записуються відносно незалежних контурів, конфігурація яких визначається вибраним деревом графа. Окремий контур може містити тільки одну хорду. Для контуру, який містить джерело струму, рівняння не записується (контур III, рис. 2.2). Отже, кількість рівнянь за ЗНК:

n_ЗНК = n_Х – n_ДС = n_Г – (n_В – 1) – n_ДС.

У нашому випадку n_ЗНК = 8 – (5 – 1) – 1 = 3 і рівняння мають вигляд:

– для І контуру: – U_Г –U_R1 –U_С1 = 0;

– для IІ контуру: U_R1 + U_L1 +U_L2 + U_R2 = 0;

– для ІV контуру: –U_R2 – U_R3 + U_С1 = 0;

Виразимо напруги на резисторах і котушках індуктивності через відповідні струми:

, .

Тоді з урахуванням заміни:

Об’єднаємо рівняння ЗТК і ЗНК у систему рівнянь. Урахуємо, що .

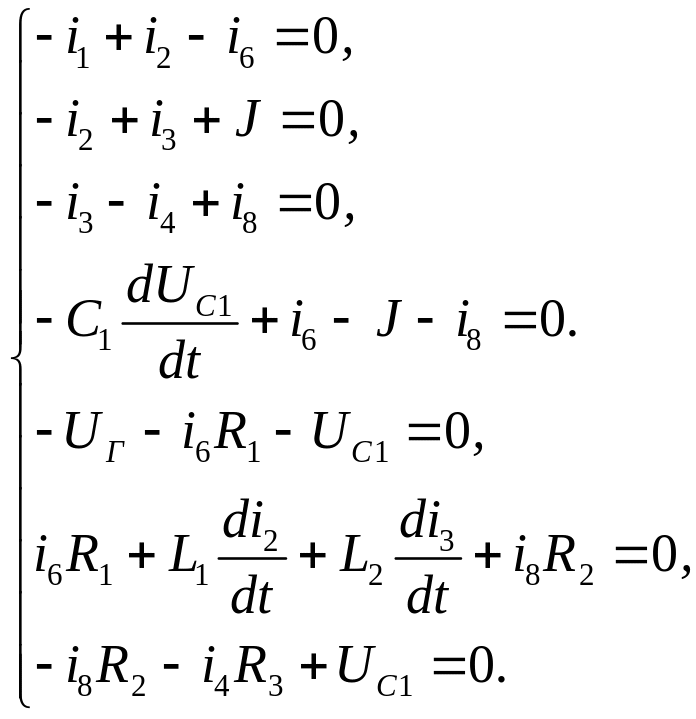
Отже, маємо сім невідомих величин (i₁, i₂, i₃, i₄, i₆, i₈, U_C1) і сім рівнянь.