Общее уравнение прямой

Определение. Нормальный вектор прямой – это любой ненулевой вектор, лежащий на любой прямой, перпендикулярной данной.

Определение. Направляющий вектор прямой – это любой ненулевой вектор, лежащий на данной прямой, или на параллельной ей прямой.

Из определения следует, что существует бесконечно много направляющих векторов заданной прямой. Все направляющие векторы заданной прямой коллинеарны, т.е. если а – направляющий вектор, то а, где также является направляющим вектором.

Лемма. Любой нормальный вектор прямой перпендикулярен любому направляющему вектору этой прямой.

Теорема. Уравнение есть уравнение прямой линии, которое называется общим уравнением прямой, где - произвольные числа, причём , (т.е. не равны нулю одновременно).

Доказательство.

Следствия из теоремы.

1) Если прямая задана общим уравнением: , где , то вектор n является вектором нормали прямой.

2) В качестве направляющего вектора прямой, заданной общим уравнением, можно взять любой вектор р, ортогональный n, например,

р .

3) Если известен направляющий вектор р , то в качестве вектора нормали можно взять вектор n .

4) Две прямые перпендикулярны, если их направляющие векторы (векторы нормали) ортогональны.

5) Если векторы нормали двух прямых коллинеарны, то прямые либо параллельны, либо совпадают.

6) Расстояние от точки до прямой : , заданной общим уравнением, находится по формуле:

.

Замечание. Уравнение (10.7) часто называют каноническим уравнением прямой, проходящей через две точки.

Параметрические уравнения прямой на плоскости состоят из двух уравнений: (*),

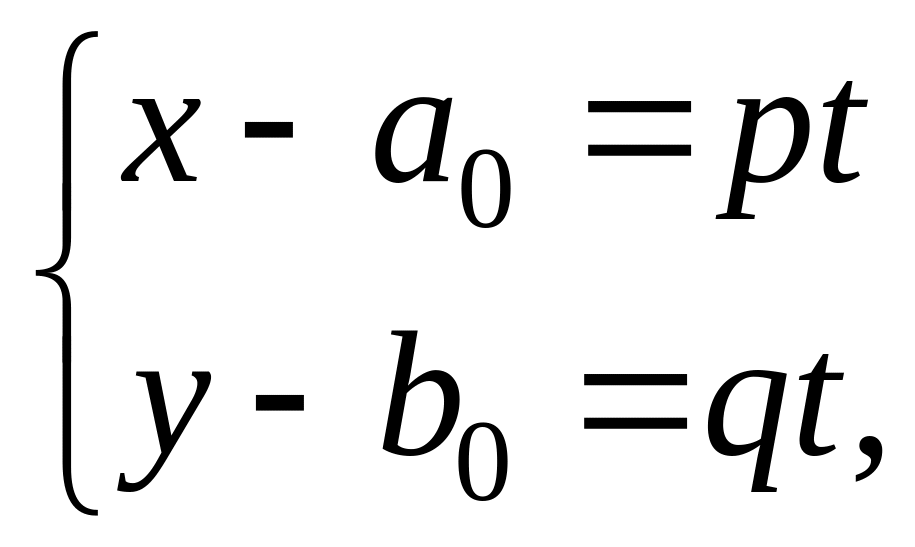где - начальная точка, - ненулевой вектор.

Исключая параметр , получим каноническое уравнение прямой:

. (**)

Замечание.

1) Если - начальная точка, - произвольная точка,

- направляющий вектор, то уравнение (**) примет вид: 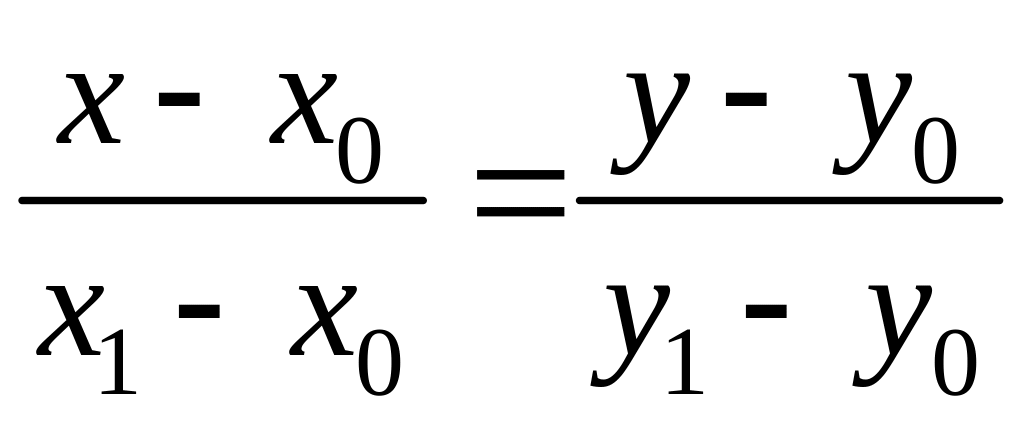- каноническое уравнение прямой, проходящей через две точки , .

2) Параметрические уравнения (*) и каноническое уравнение (**) задают прямую, одним из направляющих векторов которой является вектор с координатами

Это уравнение называется уравнением прямой в полярных координатах.

Нормальное уравнение прямой

П рименяя формулы, связывающие прямоугольные и полярные координаты:

,

получим уравнение, которое называется нормальным уравнением прямой: .

Общее уравнение прямой можно преобразовать в её нормальное уравнение . Для этого обе части общего уравнения прямой нужно умножить на нормирующий множитель:

, знак которого выбирается противоположным знаку свободного члена С. Если С=0, то прямая проходит через начало координат (р=0). В этом случае знак нормирующего множителя можно выбирать любым.

Пример. Привести общее уравнение прямой -3х+4у+15=0 к нормальному виду.

Решение. Находим нормирующий множитель .

Умножая обе части данного уравнения на нормирующий множитель, получим искомое нормальное уравнение прямой .

В данном случае p =3, cos = 3/5, sin = 4/5, = arccos(3/5).