3.2. Уравнение плоской волны.

Волновые поверхности. Плоские и сферические волны. Луч волны.

Геометрическое место точек, колеблющихся в одной фазе, называется волновой поверхностью. Волновая поверхность, отделяющая часть пространства, в которой колебания происходят, от той части, где еще нет колебаний, называется фронтом волны. Именно фронт волны перемещается со скоростью равной фазовой скорости волны. В случае одномерной синусоидальной волны уравнение волновой поверхности имеет следующий вид:

Этому условию в каждый момент времени удовлетворяет только одна точка оси ОХ, координата х которой равна:

Различным значениям фазы волны φ соответствуют различные волновые поверхности, каждая из которых в одномерных волнах вырождается в точку. Из последней формулы видно, что волновые поверхности с течением времени перемещаются в среде со скоростью, равной  , т.е. фазовой скоростью, которая равна

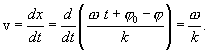
Таким образом, для синусоидальной волны скорость распостранения поверхности постоянной фазы совпадает со скоростью распространения волны.

Плоская волна — волна, фронт которой имеет форму плоскости.

Уравнением волны  называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.

(5.2.3)

      – это уравнение плоской волны.

СФЕРИЧЕСКАЯ ВОЛНА

- волна, радиально расходящаяся от нек-рой точки (источника) или сходящаяся к ней (к стоку) и имеющаясферич. волновые фронты (поверхности равных фаз).

Для скалярной волны уравнение имеет вид

Луч — линия, нормальная к волновой поверхности. Под направлением распространения волн понимают направление лучей. Если среда распространения волны однородная и изотропная, лучи прямые (причём, если волна плоская — параллельные прямые).

Понятием луч в физике обычно пользуются только в геометрической оптике и акустике, так как при проявлении эффектов, не изучаемых в данных направлениях (например дифракция, дисперсия и т. д.), смысл понятия луч теряется.

3.3. Энергетические характеристики волн: объемная плотность энергии волны, поток энергии волны, плотность потока энергии волны, интенсивность волны.

Упругая волна в процессе своего распространения вовлекает все новые и новые частицы в колебательное движение, то есть сообщает им энергию, необходимую для колебаний. Таким образом, волна переносит энергию. Эта энергия передается от одних частиц к другим со скоростью распространения волны. Будем называть плотностью энергии w - энергию колеблющихся частиц в единице объема среды. Выберем прямоугольную площадку S, перпендикулярную направлению распространения волны и построим на ней параллепипед с длиной ребра, численно равной скорости v распространения волны (рис. 1.6).

Рис. 1.6

Волна, вошедшая в этот параллепипед через основание, пройдет его за одну секунду и сообщит всем частицам его объема Sv энергию, равную w Sv. Энергию Ф, переносимую волной в единицу времени через площадку, перпендикулярную направлению распространения волны, называют потоком энергии.

Ф = w Sv (1.31)

Поток энергии - скалярная величина (измеряется в ваттах). Поток энергии в различных точках среды может иметь разную величину. Для локальной характеристики переноса энергии вводится векторная величина j - плотность потока энергии , численно равная энергии переносимой волной в единицу времени через единичную площадку, перпендикулярную направлению распространения волны. Из определения следует, что

j = Ф/S = w v

В векторной форме

j = w v (1.32)

Вектор j плотности потока энергии упругой волны называют также вектором Умова . Среднее по времени значение j _ср плотности потока энергии называют интенсивностью I волны.

I = j _ср (1.33)