Evaluation of the accuracy of results of indirect measurements

In general, the target value is a function of one or more variables. For example, the electric current in a conductor is a function of the potential difference at the ends of the conductor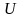 , and the conductor resistance R. Therefore, for the determination of this magnitude must first conduct a series of direct measurements of auxiliary variables, and then, using the formulas of physical laws to calculate the required amount. In this case we speak of indirect measurements.

Let the unknown quantity A is a function of the measured value x:

                        A=х (1.2.3.)

The absolute error of the measured value of A leads to mistakes . Decomposition of the right side in a Taylor series gives:

(1.2.4.)

We restrict ourselves to two terms of this series, as the other members are infinitesimal of a higher order. Then:

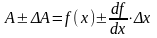(1.2.5.)

According to (1.2.3), we have:

(1.2.6.)

That is a function of the absolute error is equal to the product of the derivative of this function, the absolute error of the argument. Let the unknown quantity A depends on n variables:

(1.2.7.)

Then the differential of a function of several variables can be expressed as:

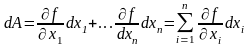(1.2.8.)

where 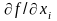- the partial derivatives. In calculating the last 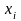arguments except considered constant and largest differentiation is the same as the function of one variable.

Instead of the absolute error is often convenient to calculate the relative error. Relative error can be represented as:

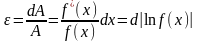(1.2.9.)

When the function  х, as is often the case, a one-term (logarithmic) form, and the derivation of formulas and calculations on them it is easier if you use a rule (1.2.9.). Expression (. 1.2.8) can be used to find errors, if we replace the differential sign for the sign error:

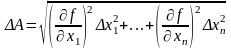(1.2.10)

or

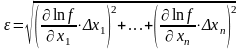(1.2.11.)

The overall result is written as:

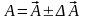(1.2.12.) Thus, to determine the error of indirect measurements following results:

1.Prologarifmirovat calculation formula.

2.Vzyat total differential of both sides.

3.Please replace the sign of d to , sign all minus signs on the plus sign.

4.Po formula (1.2.11.) To find the relative error.

5. Knowing , determine the absolute error:

A = ± ΔA (1.2.13).

6. The result is written in the form (1.2.12.).

The absolute error of the result should be rounded to one significant figure, but the result of the measurement rounded to the order in which the error begins.

As an example, consider the calculation of the volume of a sphere. He is

(1.2.14.)

where R-radius of the sphere. Directly measured R-radius of the sphere. The volume of a sphere V- value of indirectly measured.

Let R measured with calipers, the price of which is 0.1 mm division. The measurement result based on the error has the following meaning:

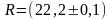                                      мм (1.2.15.)

Now calculate the volume V. It is equal to V = 45806,5mm3. Next error is calculated as :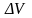

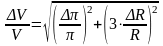(1.2.16.)

As for the error, it can be done any number of small, if you take a sufficient number of characters. Then they can be neglected. Finally:

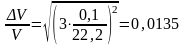(1.2.17.)

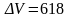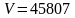and мм³, мм³.

Absolute error necessarily result should be rounded to one significant figure, and the measurement result is rounded to-order (in this example, V), where the error begins. In this case, to be rounded up to hundreds. The final test result written as follows:

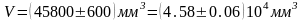( 1.2.18.)