Job number 1
1. Simple measurement and processing
1.1.Obrabotka results of repeated direct measurements
Accessories Pendulum, stopwatch.
The purpose of familiarization with the method of processing the results of repeated direct measurements such as measurement data period mathematical pendulum, to determine the most probable value of the measured value, the standard deviation, the confidence interval for a given reliability.
Brief details of the theory of measurement are divided into direct and indirect. Direct measurements are made using instruments that measure itself investigated value. So, you can find lots of bodies with the help of weights, length - measured with a ruler, and time - stopwatch. Measurement of body density by their weight and volume, speed of the train - based on the path traveled for some time, belong to the indirect measurements.
Every dimension of the imperfection of human senses and instruments sopryazhno with errors. In all dimensions allowed some bugs, so the measurement results do not give us the true, but only the approximate value of the measured value. Establishment of allowable measurement error range in which lies the true value of the measured quantity is a prerequisite of the experiment reliability. Measurement errors are divided into blunders, systematic and random.
Slips occur due to a malfunction of the device or inattentive observer, in violation of the experimental procedure and conditions for its implementation. In most cases, faults are clearly visible, as matching their samples are very different from other similar samples. The result of the measurement comprising the mistake should not be taken into account when processing the data - it should just be discarded.
Systematic errors are caused by faults or inaccuracies calibration of measuring instruments, when used for the calculation of inaccurate data, and also due to the imperfections of the measurement method. These errors affect the measurement results are always one-sided (only increasing or decreasing them). It is obvious that the influence of the systematic errors can not be reduced by increasing the number of dimensions. However, if the nature and character of systematic errors are known, their influence on the measurement result can be accounted for by introducing amendments and deleted.
Random errors are caused by fluctuations of the measured values, their appearance can not be prevented, so they can have some impact on the individual measurements, the result of changing in both directions, that is, and increase or decrease them. They are subject to statistical laws, so the impact of random errors in the measurement result can be accounted for, or greatly reduced. By applying the laws of probability theory, we determined the most probable values of the measured values and possible deviations from these values.
Evaluation of the accuracy of the result of repeated direct measurements
Let
the repeated measurement
of a physical quantity
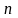of its values were obtained:
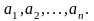Then, the arithmetic mean of all values
obtained, which is the most significant as well
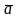
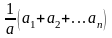
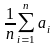(1.1.1.)
Each individual measurement differs from the arithmetic mean by an amount equal
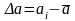(1.1.2.)
The
deviation is called
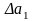absolute error of i - that dimension.
The
absolute error
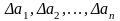of individual measurements take both
positive and negative values.
From
experience we know that the probability of error is smaller, the more
it. Additionally, if a very large number of measurements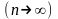
,
the errors are the same magnitude but different in sign occur equally
often. Speed reducing the probability of occurrence and its increase
is characterized by
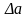a dispersion of error. It is
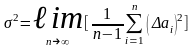(1.1.3)
The
less
,
the less the likelihood of greater in magnitude of random error
,
less scatter of individual values.
(1.1.4)
Consequently,
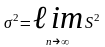(1.1.5)
The square root of the variance measurement is called the mean square error
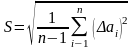(1.1.6)
If, instead of the expression (1.1.6) to substitute the value of the equation (1.1.2), then
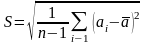(1.1.7)
In
the expression (1.1.7) includes the value
,
not
.
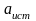The very magnitude
determined some oshibkoy.Sredney square
error of the arithmetic mean of a number of measurements is the value
equal to the
mean square of the number of measurements.
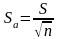(1.1.8)
Or
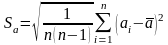(1.1.9)
Estimates
of variance
and
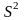are marginal, fair, just
,
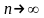ie, at large
.
For small values of these estimates are themselves random, at best,
only determine the order of magnitude of dispersion.
Measurement
processing task is to determine the range of up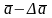
to
+
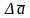, which concluded with a probability of the true
value
of the measured value. The interval from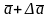
to
is called the confidence interval is called
a confidence probability (reliability). If the number of measurements
is sufficiently large, then the confidence level expresses the
proportion of the total number of measurements in which the measured
value is within the confidence interval.
For example, if a measurement is made of
100, then the confidence level
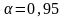of 95 measurement values were obtained, without departing from its
scope. Of course, the greater reliability is required, the more turns
the corresponding confidence interval, and conversely, the larger the
confidence interval is given, the more likely that the measurement
results will not go beyond it.
It
follows from the theory of errors that a large number of measurements
(over a hundred) confidence level interval of equal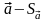
to
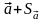68%, and the interval from
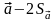to
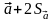is 95%. When submitting any of the measured values of the main lead
and the confidence interval of the probability of corresponding to
this interval.
In cases where the number of measurements is small, there are no conditions for the existence of a strict statistical regularities that underlie the determination of random errors. This leads to the fact that the values of the standard deviation of the average Sa, calculated from (1.1.9) is not accurate and the more inaccurate the smaller number of measurements . Therefore, to garanatirovat that the true value of the measured value with a given probability is within the confidence interval must be increased. With a limited number of measurements are not taken abroad Sa confidence interval Sa, and а:
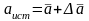(1.1.11)
The measurement results can not be compared values dissimilar to each other by their absolute errors. For comparison, the measurement accuracy of these values is entered relative error - the ratio of absolute error to the mean value of the measured value.
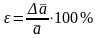(1.1.12)
According to the relative error is convenient to compare the results of measurements of similar values.
Values Ctyudenta coefficients.
Table 1.1.1
|
0,6 |
0,7 |
0,9 |
0,95 |
0,99 |
2 |
1,38 |
2,01 |
6,31 |
12,71 |
63,66 |
3 |
1.06 |
1,3 |
2,92 |
4,30 |
9,92 |
4 |
0,98 |
1,2 |
2,35 |
3,18 |
5,84 |
5 |
0,94 |
1,1 |
2,13 |
2,78 |
4,60 |
6 |
0,92 |
1,1 |
2,02 |
2,57 |
4,03 |
7 |
0,90 |
1,1 |
1,94 |
2,45 |
3,71 |
8 |
0,90 |
1,1 |
1,90 |
2,36 |
3,50 |
9 |
0,90 |
1,1 |
1,86 |
2,31 |
3,36 |
10 |
0,90 |
1,1 |
1,83 |
2,26 |
3,25 |