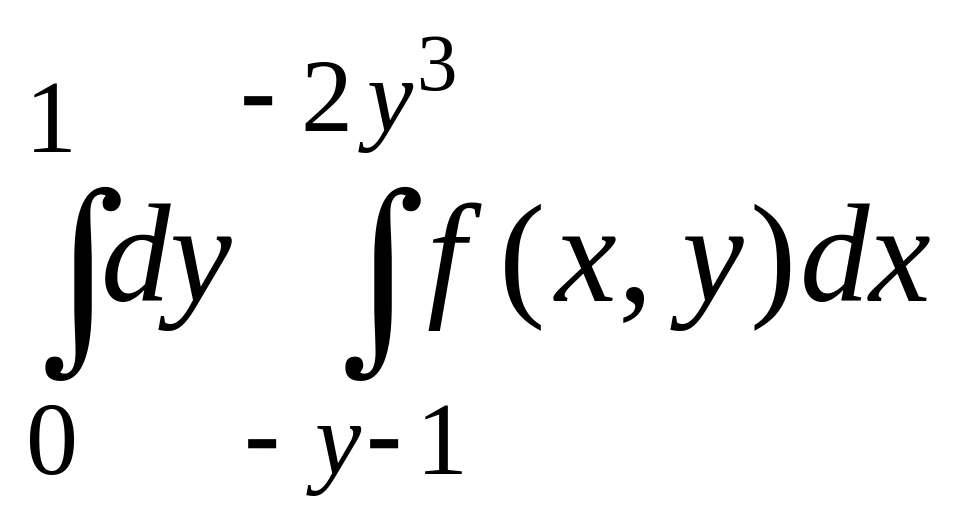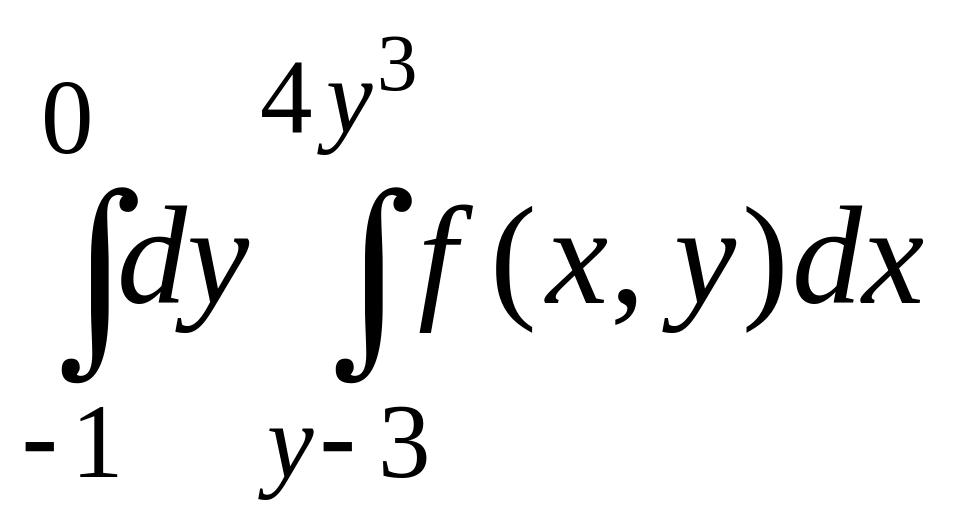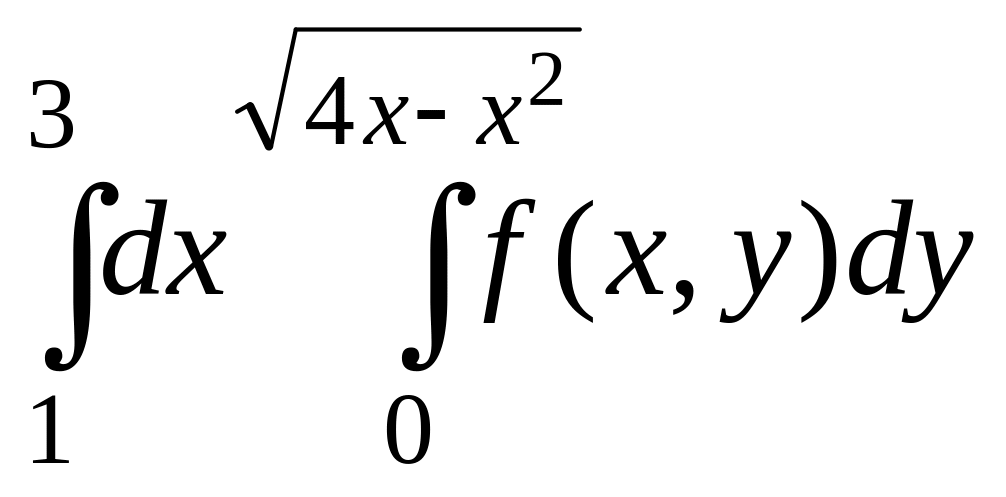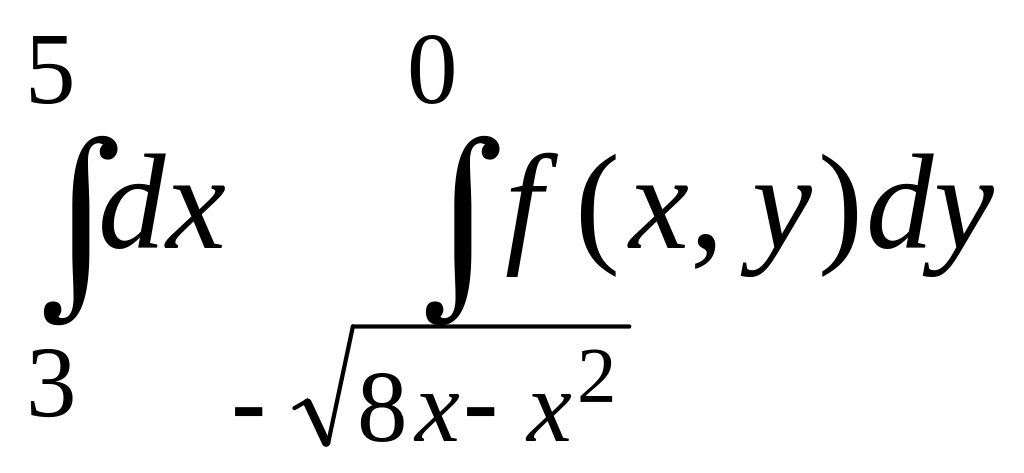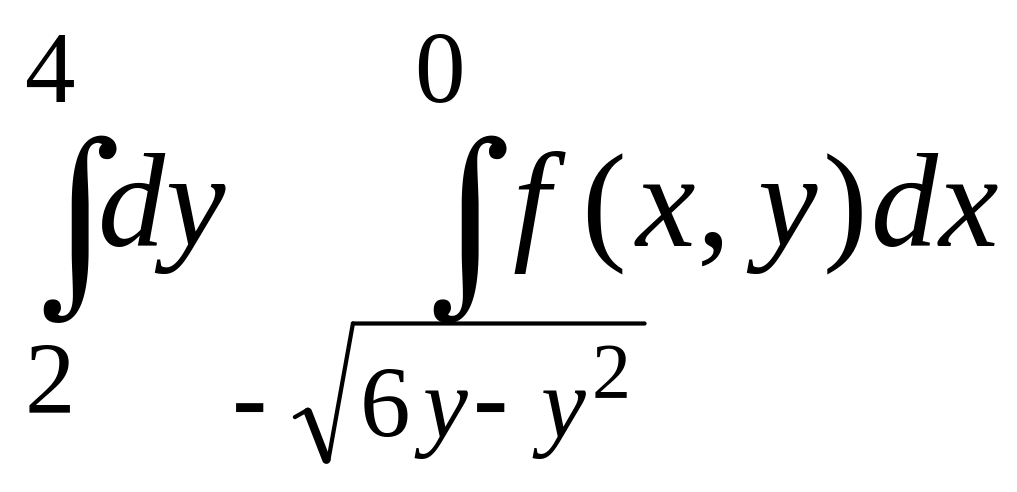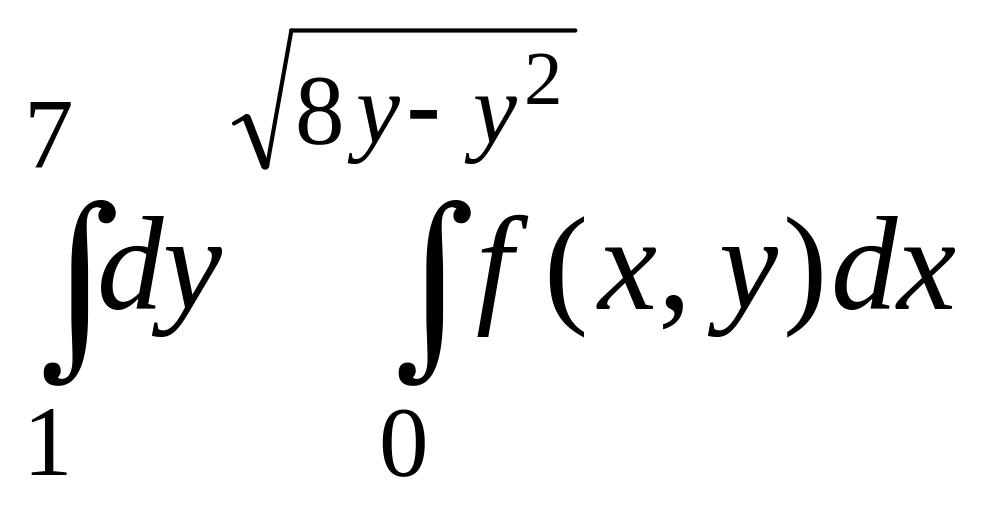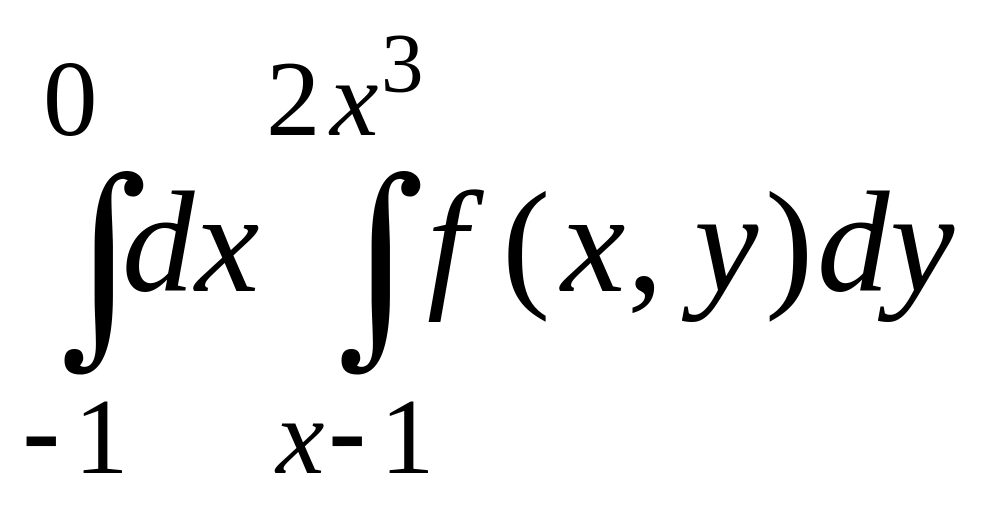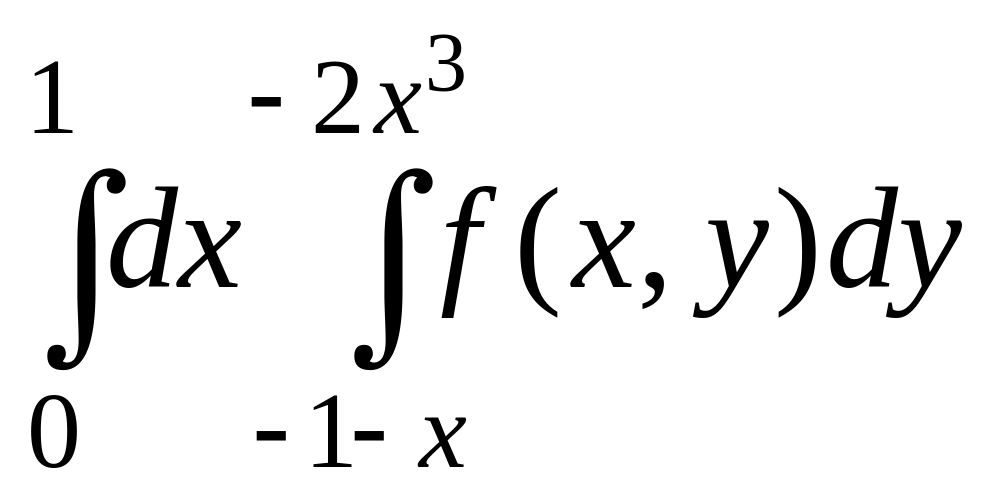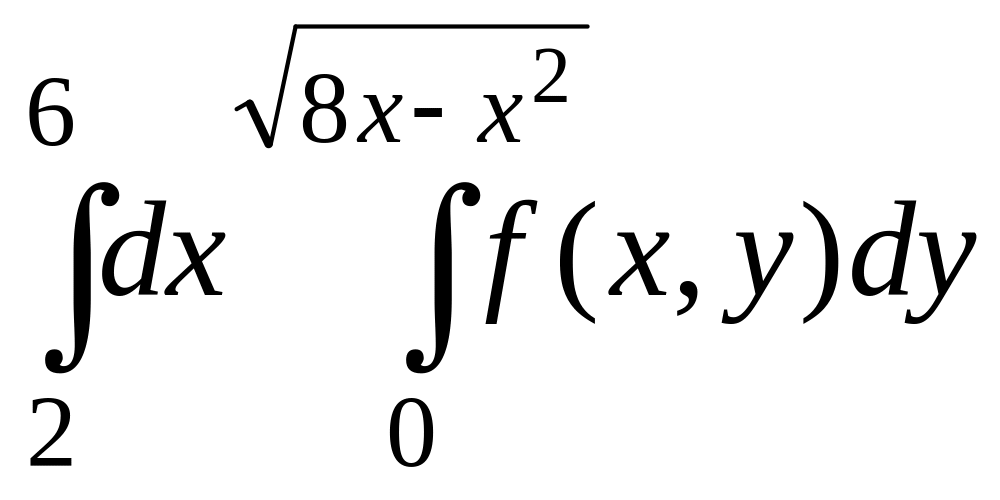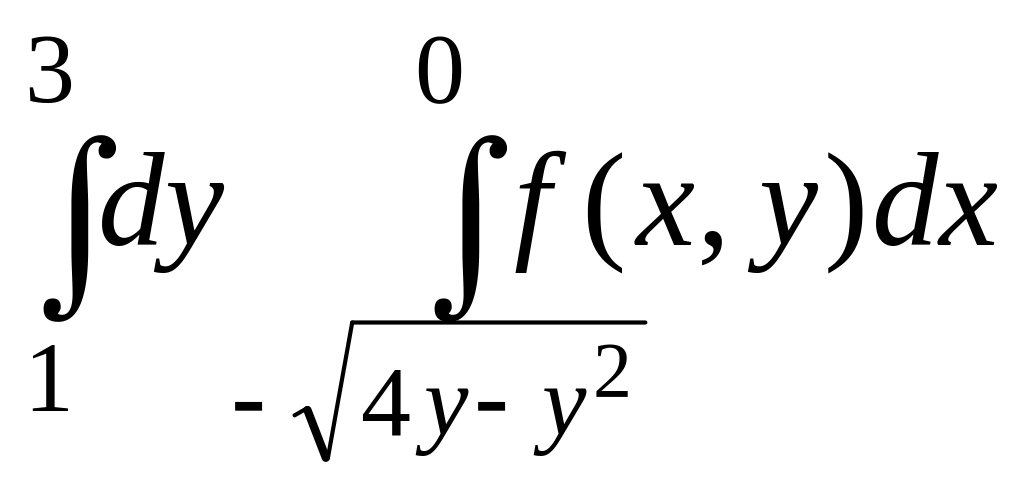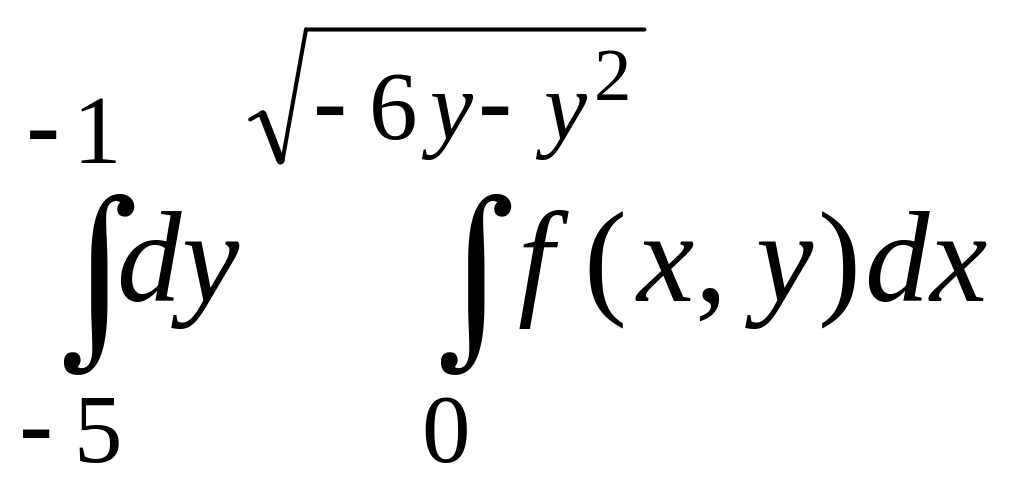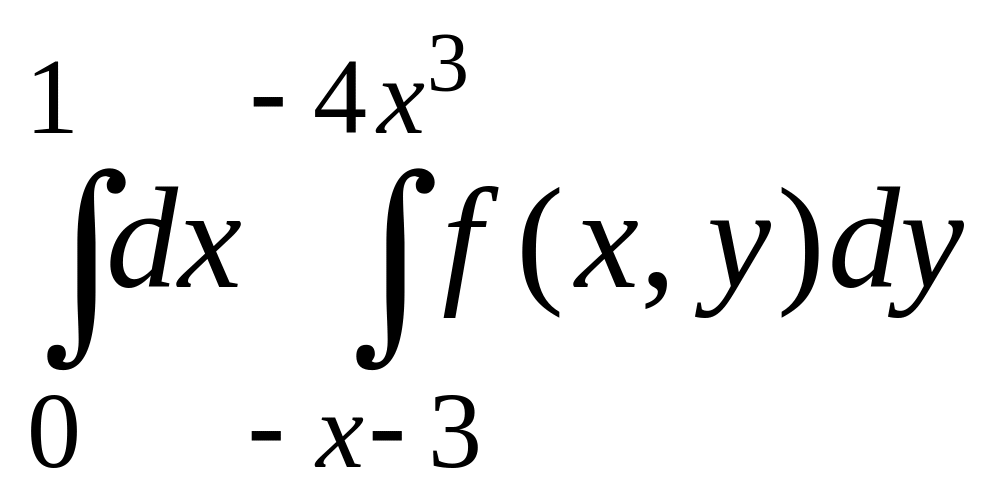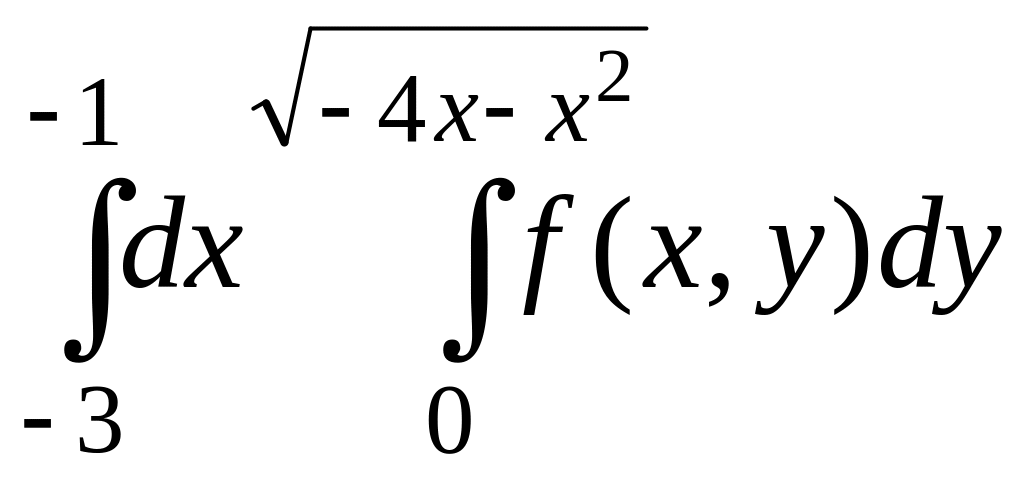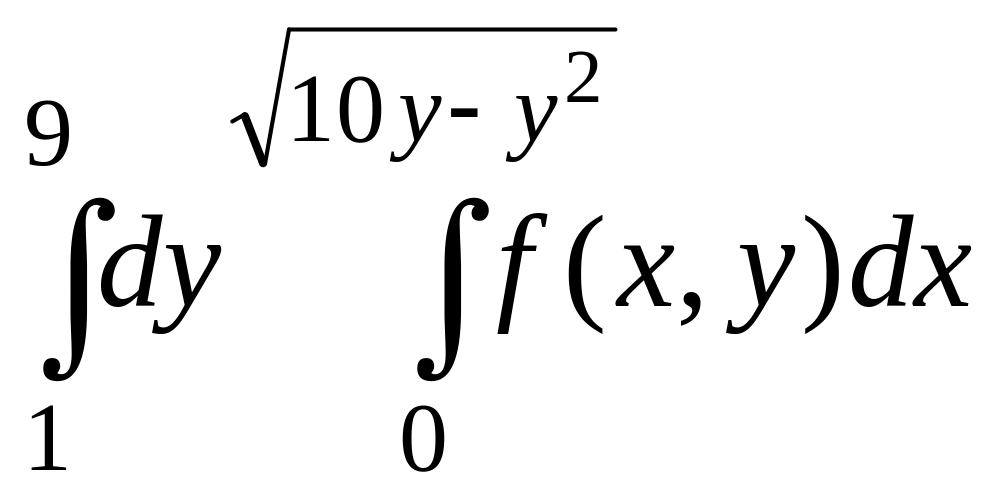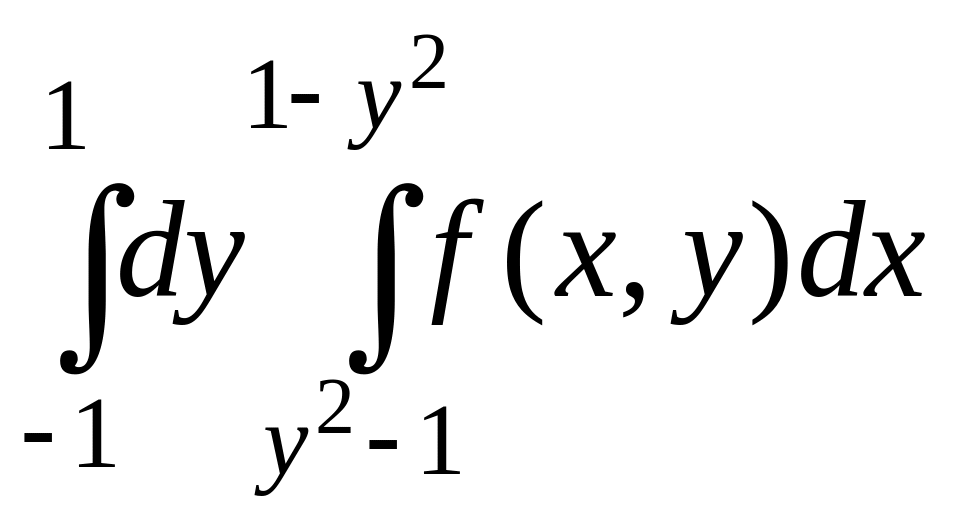Математика Учебно-практическое пособие для студентов зфо по направлению подготовки «Строительство»

Раздел 3

Приведен теоретико-справочный и прикладной учебно-методический материал по кратным, криволинейным и поверхностным интегралам, элементам теории поля, числовым и степенным рядам. По каждой теме рассмотрены решения типовых задач. Представлены задания контрольной работы по соответствующим темам для студентов ЗФО направления подготовки 08.03.01 «Строительство». Приведена рекомендуемая учебная и учебно-методическая литература для более детального изучения студентами с вышеперечисленными разделами математики.

УДК 51

ББК 22.1я73

Тема 1: «Кратные интегралы»

Теоретический минимум

1. Определение двойного интеграла.

2. Геометрический смысл двойного интеграла.

3. Физический смысл двойного интеграла.

4. Замена переменных в двойных интегралах.

5. Якобиан.

6. Определение тройного интеграла.

7. Геометрический смысл тройного интеграла.

8. Физический смысл тройного интеграла.

9. Тройной интеграл в цилиндрических координатах.

Задание № 1

Изменить порядок интегрирования в данном повторном интеграле. Выполнить чертеж области интегрирования.

Номер варианта	Повторный интеграл	Номер варианта	Повторный интеграл
1		2
3		4
5		6
7		8
9		10
11		12
13		14
15		16
17		18
19		20
21		22
23		24
25

Справочный материал к заданию

1. Основные понятия и определения.

Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.

Пусть в замкнутой области D плоскости Oxy задана непрерывная функция z = f(x, y).

Рис. 1

Разобьем эту область произвольным способом на n частичных областей с площадями s₁, s₂, … , s_n. Диаметры этих областей обозначим d₁, d₂, … , d_n (диаметром области называется наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку M_k(x_k; y_k) и умножим значение функции в точке на площадь этой области.

Интегральной суммой для функции f(x, y) по области D называется сумма вида

… + . (1)

Если при неограниченном увеличении n (n , max ) интегральная сумма имеет определенный конечный предел I = , не зависящий от способа разбиения D на элементарные области и от выбора точек в пределах каждой из них, то этот предел называется двойным интегралом от функции f(x, y) в области D и обозначается как:

I = = . (2)

Двойной интеграл обладает всеми основными свойствами обыкновенного определенного интеграла: область интегрирования двойного интеграла можно разбивать на части, двойной интеграл от суммы функций равен сумме двойных интегралов от всех слагаемых, постоянный множитель можно выносить за знак двойного интеграла.