Лекція № 4

4. Інтерполяція функцій

4.1. Математична постановка задачі інтерполювання

Однією з важливих задач в процесі математичного моделювання є обчислення значень функції, які входять до математичного опису моделі. Функції, що застосовуються в математичних моделях, задаються як аналітичним способом, так і табличним, при якому функції відомі тільки при дискретних значеннях аргументів.

Припустимо, що задано множину дійсних абсцис х₁, х₂, …, х_n і відповідні ординати у₁, у₂, …, у_n, при чому х₁ < х₂ <… < х_n , а кожне у_і – деяке дійсне число, яке пов’язане з х_і та визначене або математично, або є результатом якихось спостережень.

Задача одновимірної інтерполяції полягає в побудові функції f, такої, що для всіх і, і при цьому має приймати "розумні" значення для всіх х, що знаходяться між заданими точками. Критерій розумності змінюється від задачі до задачі і йому, можливо, ніколи не буде дано точного визначення.

Якщо походять від гладкої математичної функції і похибки в них не перевищують рівня округлень, то можна розраховувати, що задача має задовільне рішення.

Цілі інтерполяції різноманітні, але майже завжди в її основі – бажання мати швидкий алгоритм обчислення значень для всіх х, що не містяться в таблиці даних Компактна таблиця даних і невелика підпрограма інтерполювання можуть замінити доволі довгу таблицю значень функції. Часом треба знаходити значення або в проміжних точках або обчислювати інтеграл від функції по довільному підінтервалу інтервалу .

Подібні задачі формалізуються як математичні задачі інтерполювання. Точки х₁, х₂, …, х_n називаються вузлами інтерполювання. Процес обчислення значень функції в точках х, відмінних від вузлів інтерполювання, називають інтерполюванням функції .

П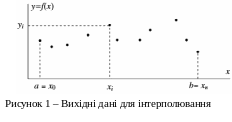 риклад даних, приготовлених для інтерполяції наведено на рис. 1. Чорні кола на цьому рисунку відповідають значенням у_і функції у вузлах інтерполяції х_і.

Г еометрично задача інтерполювання для функції однієї змінної означає побудову кривої, яка проходить через точки площини (рис. 2) з координатами . Але з розгляду рисунку інтуїтивно випливає, що через задані точки можна провести безліч кривих. Таким чином, задача пошуку функції по скінченному числу її значень є доволі невизначеною.

У випадку, коли вибирається в класі степеневих функцій, інтерполяція називається параболічною. Цей спосіб наближення базується на тому, що на невеликих відрізках функція може бути достатньо добре подана параболою визначеного порядку.

Для задачі інтерполювання дуже важливим є визначення того, як має вести себе прийнятна функція між заданими точками. В кінці кінців ці точки можуть бути інтерпольовані нескінченною множиною різних функцій, і треба мати деякий критерій вибору. Зазвичай критерії формулюються в термінах гладкості і простоти; наприклад, функція f має бути аналітичною і максимальне значення на всьому інтервалі повинно бути наскільки можливо малим, або f має бути поліномом найменшого степеня, і т. п.

Зазначимо, що при інтерполюванні виникає ряд задач:

1) вибір найбільш зручного способу побудови інтерполяційної функції для кожного конкретного випадку розв’язання задачі інтерполяції;

2) оцінка похибки інтерполювання заданої функції;

3) оптимальний вибір вузлів інтерполяції для отримання мінімальної похибки.