4. Правило Верещагина

Вычисление перемещений по формуле Мора существенно уп­рощается, если одна из эпюр прямолинейна, а жесткость балки постоянна. Тогда при определении перемещений интеграл Мора вычисляют графоаналитически по правилу А. Н. Верещагина, предложенному им в 1925 г.

Основное преимущество этого правила состоит в том, что при его помощи можно обойтись без составления уравнения момен­тов и без интегрирования их произведений. Эти трудоемкие опе­рации заменяются простейшими геометрическими вычисления­ми, заключающимися в «перемножении эпюр» изгибающих моментов от действительной и единичной нагрузок.

Уравнения изгибающих моментов и , входящие в форму­лу интеграла Мора, – это некоторые функции от х: = f₁(x), = f₂(x), а графики этих функций – эпюры и , (рис. 3).

Подынтегральное выражение формулы (2) можно представить в виде:

dx. (3)

f₁(x)

у

ц.т.

x

x

dx

у

f₂(x)

у _с=k x_c+b

l

x_c

x

Рис. 3. Графики функций f₁(x) и f₂(x)

Предположим, что на участке длиной l функция f₁(x) изменяется по произвольному, а функция f₂(x) – по линейному закону.

Используя аналитическую запись линейного закона f₂(x) = k x + b, выражение (3) представим в виде:

dx = f₁(x) dx = k f₁(x) dx + b

Произведение f₁(x)dx = d представляет собой площадь элементарной криволинейной трапеции, заштрихованной на рис. 3.

Значит, первый интеграл – статический момент площади относительно оси у и равен произведению площади на координату её центра тяжести у_с. Второй интеграл выражает собой площадь эпюры =

Таким образом , k x + b) = ,

где k x + b – ордината у_с эпюры под центром тяжести .

Следует помнить, что ордината у_с берется только из прямолинейной эпюры. Окончательно формула для определения перемещений принимает вид: .

Перемещение в пределах рассматриваемого участка положительно, если площадь и соответствующая ордината у_с расположены по одну сторону от оси данного участка, и отрицательно, если они расположены по разные стороны.

По правилу Верещагина нельзя определить перемещение, если обе эпюры, и , криволинейные или жесткость элемента на рассматриваемом участке переменна. При сложном очертании эпюры или их делят на простые эпюры, площади и положение центра тяжести которых известны.

Для вычисления перемещений по правилу Верещагина надо выполнить следующие действия:

1. построить эпюру от реально приложенной нагрузки. Эту эпюру называют грузовой.

2. приложить единичный силовой фактор (силу или момент) в точке, где необходимо определить перемещение поперечного сечения.

3. построить эпюру изгибающих моментов от единичного силового фактора.

4. перемножить площадь грузовой эпюры на ординату взятую с эпюры от единичного силового фактора под центром тяжести (ц.т.) площади грузовой эпюры.

5. Полученное произведение разделить на жесткость поперечного сечения балки EI.

Пример 4.1.

Определить прогиб в т. К и А балки нагруженной силой Р.

х

у

l

Р

v_А

х

В

А

К

а)

l / 2

v_К

1

С

ЭМ_{и от 1}

ЭМ_{и от Р}

–

–

В

В

Р

К

К

D

б)

-Р · l

E

в)

- l

Рис. 4.Схема балки и эпюры М_и для определения перемещения т. К

I

Решение.

.. Определение перемещения т. К.

Балка имеет один участок. Для составления уравнения М_и надо воспользоваться методом сечений. 0 х l

1.Построение эпюры М_и от действующей нагрузки. Эта эпюра называется грузовой.

Уравнение М_и. М_и = – Р · х, при х = 0 М_и = 0, при х = l М_и = – Р · l

2.К точке К прикладывается единичная сила. Максимальный изгибающий момент возникает в заделке. М_и = – 1· l = – l. Под грузовой эпюрой строят эпюру от единичной силы.

3.Определение площади грузовой эпюры и положения её центра тяжести относительно левого края балки (см. рис.4 б).

l · (– Р · l) = – . х_c =

4.Вычисление ординаты на эпюре М_и от единичной силы, взятой под центром тяжести грузовой эпюры.

_.

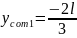5.Определение прогиба в точке К.

_к = .

Положительный знак перемещения точки К означает, что направление перемещения совпадает с направлением единичной силы.

Если эпюра заданных сил линейная, то операция перемножения обладает свойством коммутативности. В этом случае безразлично, умножается ли площадь первой эпюры на ординату второй или площадь второй эпюры на ординату первой.

Использование свойства коммутативности при расчете перемещения т.К.

1.Определение площади второй эпюры

.

2.Из подобия треугольников на грузовой эпюре можно составить соотношение:

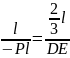, DE = .

3.Произведение площади второй эпюры на ординату DE первой эпюры:

DE = .

4. Перемещение т. К с учетом жесткости:

_к = .

I I. Определение перемещения т. А.

а) умножением площади грузовой эпюры на ординату, взятую с эпюры единичной силы.

у

l

l / 2

х

Р

v_А

х

В

А

К

а)

h

ЭМ_{и от 1}

В

Р

К

К

У_С1

–

С_тр

б)

ЭМ_{и от Р}

a

-Р · l

1

А

В

D

х

–

С₁

в)

E

Рис. 5.Схема балки и эпюры М_и для определения перемещения т. А

1. Строим грузовую эпюру от действия силы Р.

2. К т. А прикладываем единичную силу и строим эпюру М_и (рис. 5.в.)

0 х l / 2. М_и = –1· х = – х. При х = 0 М_и = 0. При х = М_и = .

3. Грузовая эпюра над эпюрой от единичной силы имеет форму трапеции. Площадь трапеции определяют по формуле:

· h, где а, b и h – стороны трапеции.

Для определения стороны b, составим соотношение из подобия треугольников .

, отсюда b = = .

· = =

Площадь трапеции имеет знак минус, так как грузовая эпюра отрицательная.

4. Расстояние Х_{С тр}, от основания трапеции а до центра тяжести можно определить используя выражение:

Х_{С тр} = .

5. Для определения ординаты DE на эпюре от единичной силы под центром тяжести трапеции вычисляем расстояние АD.

АD = . DE = АD = .

Знак минус у ординаты DE появился потому, что она находится ниже нулевой линии эпюры.

6. Произведение на DE: ·

7. Перемещение т. А с учетом жесткости EI: _А =

В данном примере перемещение _А получилось с положительным знаком, значит прогиб балки происходит в направлении единичной силы.

Сравним перемещения точек А и К составив соотношение:

3,2.

Перемещение точки А в 3,2 раза меньше перемещения точки К.

б) определение перемещения точки А перемножением площади эпюры М_и от единичной силы на ординату взятую с грузовой эпюры.

1. Площадь эпюры от единичной силы (Рис.5 в):

Координата центра тяжести этой эпюры: Х_{С 1} = .

2. Ординату У_С1 на грузовой эпюре над С₁ можно определить из соотношения сторон треугольников: , отсюда: У_С1 =

3. На участке АК площадь эпюры М_и от единичной силы равен нулю, поэтому результат перемножения эпюр будет равен нулю. Перемножаются эпюры только на участке АВ. _А = .

Пример 4. 2.

Для балки представленной на рисунке 6 требуется определить прогиб в точке С и углы поворота опорных сечений. Принять: l = 5 м, q = 800 Н/м,

I = 166 см⁴, Е = 2 10⁵ Н/мм², АС = l/2.

Решение.

1.Определяем реакции опор, используя уравнения равновесия.

, , .

, , .

Проверка.

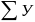= 0, , , 0 = 0.

2. Строим эпюру изгибающих моментов. Весь пролет представляет собой один участок (Рис.6а). 0 х l.

у l/2 vc х RB'= RA'= ц.т. в) б) а) В А F E D M=1 А RA" В RB" В А C GА 1 RA RB х l q ΘВ А C х ΘА В

Ми = RA x q x = 0, Ми = 0 x = l, Ми = 0 x = , Ми = . 3. К заданной балке, к точке определения прогиба прикладываем единичную силу и строим эпюру Ми (Рис.1б). Единичная эпюра состоит из двух одинаковых линейных участков. Грузовую эпюру разбиваем на две одинаковые части. Площадь и положение центра тяжести каждой из этих частей даны в справочной таблице. В данном случае достаточно выполнить перемножение эпюр для одного участка и результат удвоить.

Рис.6.Схема балки и эпюры М_и для определения

линейных и угловых перемещений

Если площадь всей грузовой эпюры равна h , то площадь её половины составит .

Ординату EF под центром тяжести грузовой эпюры можно вычислить из соотношения сторон треугольников единичной эпюры: =

Максимальный момент изгибающий от единичной силы равный отрезку CD получается в из уравнения М_и , при x = : М_и = R_A^' .

Из соотношения сторон треугольников :

EF = .

Произведение = .

Удвоенное произведение данного значения: .

Прогиб (перемещение) балки в точке С: _C = .

Прежде чем подставить числовые данные, надо привести их к соответствующим размерностям: l =5м = 5000мм, q = 800Н/м = 0,8Н/мм,

I = 166см⁴ = 166 10⁴ мм⁴.

Жесткость материала балки: EI = 2 10⁵ 166 10⁴ = 332 10⁹ мм⁴ (Н мм²)

_C = 19,6 мм.

4. Угол поворота балки в сечении А.

Прикладываем единичный момент в т. А (Рис.6в) и определяем силы реакций в опорах. , R_A^" l = 0, R_A^" = = .

, R_B^" l = 0, R_B^" = = .

Проверка. = 0, R_B^" R_A^" =0, , 0 = 0

Строим эпюру М_и от единичного момента. Эта эпюра линейна по всей длине балки М_и = R_A^" x +M, при x = 0 М_и = M = 1, при x = l М_и = R_A^" l +1=0, при x = М_и = R_A^" + M = + 1 = .

Площадь грузовой эпюры: .

Ордината эпюры единичного момента под центром тяжести грузовой эпюры равна . Произведение площади на ординату: .

Угловое перемещение балки в точке А: θ_A = .

Подставляем числовые значения параметров.

θ_A = = 0,0125 рад.

В одном радиане содержится 57,3 градуса. Угол поворота сечения А в градусах: θ_A = 0,0125 = .

Площади эпюр M_и и расстояния до их центров тяжести

Нагружения	Вид эпюры Mи	Площадь эпюры,		Расстояние до центра тяжести, ZC
	h l ZC	h l	l
	l ZC h	hl	l
	h ZC a l	hl
	ZC l h	hl	l
	l ZC h	hl	l
	l ZC h	hl	l