37

Министерство образования и науки РФ

Фгбоу впо «Тверской государственный технический университет» Кафедра «Бухгалтерский учет и финансы»

Задание к практической части курсового проекта

по дисциплине «Информационные технологии экономического анализа и аудита»

для студентов направления «Экономика» заочной формы обучения

Оптимизация программ производства и сбыта на основе применения инструментария электронных таблиц

Разработал: к.т.н., доцент Бородулин А.Н.

Тверь, 2015 Оглавление

1. Базовая модель оптимизации производственной программы 4

2. Исследование ограничений и параметризация программ производства и сбыта 19

Вопросы и задания для самопроверки 36

Задание на самостоятельную работу 37

1. Базовая модель оптимизации производственной программы

Задача планирования оптимальной по прибыли производственной программы или программы сбыта стоит перед каждым предприятием, которое имеет широкую номенклатуры выпускаемой продукции, реализуемых товаров, оказываемых услуг. В условиях рынка быстрое реагирование на изменяющиеся факторы внешней среды (спрос потребителей, ценовая политика конкурентов, возможности по обеспечению сырьем и др.) становится залогом выживаемости любого предприятия. Поэтому для оперативной корректировки краткосрочных программ и планов предприятия необходимо использование специальных математических методов, которые составляют основу специального инструментария для поддержки принятия управленческих решений и обеспечивают в перспективе достижение предприятием своих долгосрочных стратегических целей.

При составлении краткосрочной производственной программы или программы сбыта, устанавливают количество и номенклатуру выпускаемой продукции, реализуемых товаров, выполняемых работ и оказываемых услуг. Наиболее предпочтительной является такой вариант производственной или сбытовой программы, который обеспечивает наилучшие показатели по ожидаемой прибыли. Ограничивающими факторами при такой постановке задачи выступают так называемые «узкие места» производства и сбыта, существующие на предприятии. На практике в качестве «узких мест» обычно рассматривают:

• недостаточный спрос на определенные виды продукции;

• оборудование, мощность которого ниже, чем у других видов оборудования;

• дефицитные сырье и материалы;

• недостаток квалифицированных кадров и др.

В зависимости от конкретных условий работы предприятия принято выделять три возможные ситуации с наличием «узких мест» производства и сбыта:

• отсутствие «узких мест» (имеет место неполная загрузка производственных мощностей или неудовлетворенных спрос на рынке);

• наличие одного «узкого места» (например, существует всего один ограничивающий производство ресурс или низкий спрос на один вид продукции);

• несколько «узких мест» (как правило, это наиболее типичная ситуация, ведь на практике редко можно иметь «неиссякаемые» источники сырья, равное по производительности оборудование или монопольное положение на «безразмерном» рынке).

При неполной загрузке мощностей и отсутствии «узких мест» в качестве критерия определения производственной программы используют удельную маржинальную прибыль, то есть разность между ценой продукции (услуг) и переменными затратами на ее производство. В производственную программу включают все виды продукции (услуг), у которых положительная удельная маржинальная прибыль. Тогда предприятие сможет использовать все имеющиеся возможности для покрытия постоянных затрат и получения прибыли.

Очень важным обстоятельством вышеописанной процедуры составления оптимальной производственной программы является то, что использование для этих целей прибыли на единицу продукции представляется нецелесообразным, так как исключение из программы кажущихся убыточными продуктов (только потому, что на нее было отнесено больше постоянных затрат, чем на другие) может привести к потере дополнительной маржинального дохода, а в итоге и к потере прибыли. Это положение исходит из применения в системе управления методов учета затрат на основе неполной (усеченной) себестоимости (по системе директ-костинг).

В ситуации когда на предприятии существует только одно «узкое место», в силу приведенных выше оснований в качестве критерия оптимальности при составлении краткосрочной производственной или сбытовой программы целесообразно использовать относительную маржинальную прибыль, т.е. частное от деления маржинальной прибыли каждого вида продукции (услуг) на потребляемое количество того производственного ресурса, который является узким местом и за которой «конкурируют» выпускаемые виды продукции.

Включение продукции (товаров, услуг) в производственную программу (программу сбыта) осуществляется в порядке убывания относительной маржинальной прибыли, что обеспечивает оптимальное распределение ресурсов.

Если на предприятии несколько «узких мест», необходимо определить, от какой выгоды (маржинальной прибыли) отказывается предприятие, когда вместо одних видов продукции оно производит и продает другие. Для этого целесообразно использовать аппарат линейного программирования, одного из прикладных разделов исследования операций.

Все модели линейного, как впрочем и всех других видов математического программирования, имеют два общих основных свойства. Пер­вое – это наличие ограничений. В случае задачи планирования производственной программы в их качестве будут выступать рассмотренные ранее конкретные ограничения «узких мест» производства и сбыта. Второе свойство моделей линейного программирования заключается в том, что в каждой моде­ли существует единственный показатель эффективности, который необходимо максимизировать (как правило, это прибыль, эффективность или производительность) или минимизировать (обычно это за­траты или время). В моделях оптимизации показатель эффективности, который следует оптимизировать, называется целевой функцией.

Отличительной характеристикой моделей линейного программирования является условие задания ограничений и целевой функции в линейной форме, то есть в виде выражений, в которые каждая переменная задачи вместе со своим коэффи­циентом входит в виде отдельного подвыражения (переменные не умножаются, не делятся друг на друга, не возводятся в степень, отличную от единицы, нет логарифмических, экспонен­циальных или тригонометрических выражений и т.д.). Сила и привлекательность линейного программирования за­ключается в простоте формулирования на практике линейных связей (уравнений и неравенств) и доступности, а также высокой эффективности алгоритмов их решения.

При планировании продуктовой программы при заданном потенциале методами линейного программирования целевая функция задается функцией маржинальной прибыли; как и в случае ситуации с наличием на предприятии одного «узкого места», необходимо исходить из относительной маржинальной прибыли. Естественно, на практике более удобным является применения в качестве целевой функции общей прибыли, а не маржинальной. Для этих целей в целевую функцию необходимо в виде вычитаемого добавить величину постоянных затрат предприятия. Однако постоянные затраты должны присутствовать в целевой функции только как свободный член, то есть не являться коэффициентом при переменных задачи.

Приведем математическую постановку задачи линейного программирования планирования краткосрочной производственной программы (1). Данная постановка задачи дается из предположения, что вся произведенная продукция реализуется за планируемый период по установленной цене. Собственно сформулированные ограничения задачи и призваны обеспечить выполнение этого условия.

Дальнейшее рассмотрение методов планирования краткосрочной производственной программы проиллюстрируем примером.

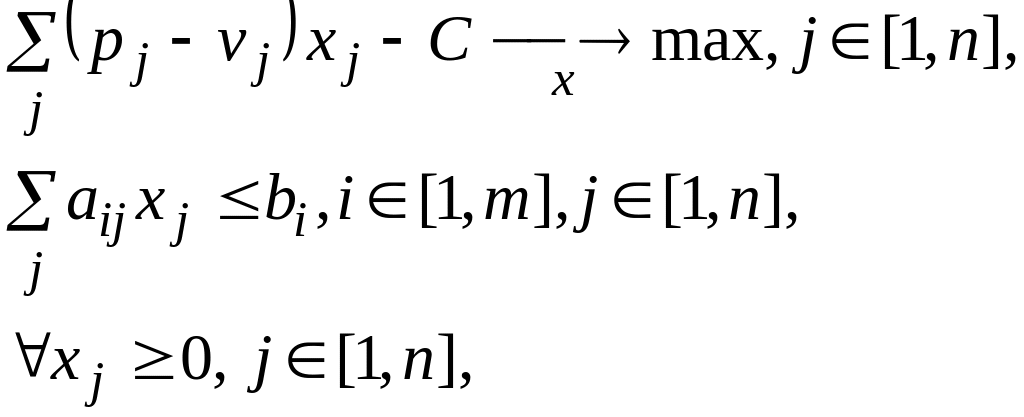(1)

где – вектор плана выпуска продукции – искомые переменные задачи;

– вектор цен реализации на продукцию;

– вектор прямых переменных затрат на продукцию;

C – сумма всех видов постоянных затрат;

– матрица потребностей в ресурсах для выпуска продукции;

– вектор доступных объемов ресурсов;

n – количество видов продукции;

m – количество видов ресурсов;

Пусть на предприятии производится три вида продукции, для каждого из которых можно определить неизменную в некотором периоде цену реализации и сумму переменных издержек в рублях:

	Продукт A	Продукт B	Продукт C
Цена реализации	245	275	345
Переменные издержки	166	185	242

Также установлена общая сумма всех постоянных затрат предприятия – 450 тыс. руб.

На практике точный расчет величины переменных издержек, относимых на конкретный вид изделия, а также суммы постоянных затрат, может быть выполнен достаточно точно благодаря используемым в системе управления методам учета затрат по неполной себестоимости. Условие постоянства цен реализации для случая планирования краткосрочной производственной программы тоже обычно выполнимо, прежде всего, именно из-за небольшого рассматриваемого горизонта планирования и легко доступной информации о ситуации, установившейся на рынке продаж конкретных товаров.

Пусть также на предприятии существует информация о нормах потребления различных видов ресурсов для производства отдельных видов продукции. Рассмотрим отвлеченный пример, не уточняя конкретное воплощение ресурсов, отметим только, что ими могут быть ограничения по возможностям оборудования, каналов снабжения, объемам спроса на рынке и другим видам «узким мест», рассмотренных ранее. Принципиально важным в практических задачах является только представление всех нормативов и ограничений в одних единицах измерения, так как обычно при нормировании используются не денежные, а произвольные натуральные показатели, например время обработки изделий или загрузка оборудования, объем доставки или хранения партий сырья и т.п.

	Продукт A	Продукт B	Продукт C	Максимальный лимит
Ресурс 1	78	96	102	1350000
Ресурс 2	203	210	264	3000000

Для решения задач линейного программирования существует большое количество аналитических способов решения, например широко известный симплекс-метод и его многочисленные модификации. Алгоритм поиска, реализованный в этих методах, основан на расчете для всех видов продукции, еще не включенных в программу, величин маржинальной прибыли, с которыми сравнивается маржинальная прибыль уже включенного в производственную программу вида продукции и считавшегося до сих пор наиболее выгодной альтернативой. После этого в программу включаются виды продукции, которые имеют большую маржинальную прибыль по «узкому месту», чем виды, уже включенные в программу. Достоинство симплекс-метода в том, что необходимые для оценки решения величины маржинальной прибыли не входят в расчеты как заданные, а определяются в процессе расчетов с учетом всех возникающих при реализации решения «узких мест». Кроме того, на каждом этапе расчетов выявляются потребности в мощностях предприятия.

В настоящее время для решения оптимизационных задач вместо аналитических и графических методов, основанных на «ручных» расчетах, выгоднее использовать современные инструментальные средства, например табличные процессоры. Кроме удобного интерфейса ввода и представления данных, в них встроены многие вычислительные алгоритмы, приспособленные для решения широкого круга задач математического и в частности линейного программирования. Поэтому для решения поставленной в нашем примере задачи воспользуемся табличным процессором (Microsoft Excel).

В состав табличного процессора Excel входит специальный инструмент «Поиск решения» – надстройка, доступная в меню «Данные», предназначенная для оптимизации моделей при наличии ограничений, в том числе моделей линейного про­граммирования. Для этого в надстройке используются методы и алгоритмы математиче­ского программирования, которые позволяют находить оптимальные решения для данных, представленных в виде электронных таблиц. В случае задач линейного программирования надстройка «Поиск решения» использует эффективный оптимизационный алгоритм, основанный на симплекс-методе.

Для создания модели линейного программирования предлагаемого примера в табличном процессоре Excel данный процесс лучше разбить на три этапа.

1. Написание и проверка символической модели линейного программирования. Модель записывается в математическом виде, что поможет при отладке окончательного варианта табличной модели в Excel. Затем анализируются форму­лировки математической задачи с целью выявления возможных логических оши­бок.

2. Создание и отладка табличной модели линейного программирования. На основе символической модели создается ее представление в Excel. Затем производится проверка полученной таб­личной модели путем задания различных значений переменных решения с целью выявить возможные очевидные ошибки (например, для заведомо допустимых ре­шений нарушаются ограничения, значения в ячейках левых частей или критерий эффективности оказываются лишенными смысла и т.д.).

3. Попытка оптимизации модели с помощью надстройки «Поиск решения». Если модель некорректно сформирована, результатом чаще всего будет сообщение об ошибке. Тогда нужно исправить модель, возможно, вернувшись к первому этапу.

Мы уже сформировали символическую модель для первого этапа (1). Поэтому теперь создадим лист Excel для представления табличной модели (рис. 1.1).

В приведенную на рис. 1.1. табличную модель занесены исходные данные из рассматриваемого примера. Для дальнейших расчетов и использования надстройки «Поиск решения» уже подготовлены специальные ячейки. Так в 14-й строке располагается вектор относительного маржинального дохода, то есть разницы между ценой реализации и переменными издержками по каждому виду продукции (С14 = C6 – C8, аналогичные формулы должны быть скопированы в столбцы D и E).

Искомые переменные нашей задачи, то есть вектор плана выпуска продукции, располагается в 16-й строке. Значения этих ячеек не содержат формул, а, наоборот, входят в качестве множителей для расчета других параметров модели. В ячейках C18:E18 располагается вектор абсолютных значений маржинальной прибыли по каждому виду продукции с учетом планируемого (еще не определенного) плана выпуска (так C18 = C14 * C16). В отдельной ячейке G18 располагается максимизируемое в нашем примере значение ожидаемой прибыли предприятия. Для ее расчета из маржинальной прибыли по всем видам продукции нужно вычесть общую сумму постоянных затрат, то есть G18 = СУММ(C18:E18) – G8 (здесь и далее в тексте будем использовать варианты функций для русскоязычной версии Excel).

Кроме этого необходимо еще и формулы в ячейки C21:E22, которые содержат данные о расходе ресурсов, требуемых для заданного выпуска продукции. Так, например, C21 = C11 * C16, а C22 = C12 * C16 и т.д. Эти ячейки понадобятся для расчета остатков ресурсов после выпуска планируемого объема продукции. Величины этих остатков в рассматриваемой модели находятся в ячейках G21:G22 и очевидно должны служить критериями правильно составленного плана, т.е. не опускаться ниже нуля. В противном случае предприятие выйдет за имеющиеся у него лимиты ресурсов, что недопустимо по условиям задачи. Формулы ячеек G21:G22 задайте самостоятельно на основании ячеек C21:E22 и G11:G12 исходя из приведенного выше описания.

Рис. 1.1. Исходная табличная модель задачи

линейного программирования планирования

Для правильного построения моделей линейного программирования средствами табличного процессора можно сформулировать следующие рекомендации:

• каждая переменная решения располагается в отдельной ячейке, ячейки груп­пируются по строкам или столбцам; каждому ограничению отводится отдельная строка или столбец таблицы (чаше всего переменные решения расположены в столбцах, а ограничения — в строках);

• переменные решения группируются в отдельный блок столбцов/строк; анало­гично ограничения группируются в свой блок строк/столбцов;

• все ячейки, содержащие переменные решения и целевую функцию, имеют за­головки в верхней части своего столбца, а все ограничения – заголовки в крайней слева ячейке своей строки;

• коэффициенты целевой функции хранятся в отдельной строке, располагаясь непосредственно под или над соответствующими переменными решения; формула для вычисления целевой функции находится в соседней ячейке;

• чтобы модель была понятней, ячейки с переменными решения и целевой функцией выделяются рамкой по границе ячеек или заливкой ячеек;

• коэффициент перед определенной переменной решения в каком-либо ограниче­нии записывается в ячейку на пересечении столбца (строки), содержащего данную переменную решения, и строки (столбца), содержащей это ограничение;

• в каждой строке ограничений за ячейками, содержащими коэффициенты дан­ного ограничения, следует ячейка, содержащая значение правой части неравенства; дополнительно может включаться ячейка с формулой вычисления остатка, то есть разности между значениями левой и правой частей неравенства, вычисляемой таким образом, чтобы она не была отрицательной при соответствии ограничению;

• ячейки, содержащие правые части ограничений, должны включать константы или формулы, в которые не входят переменные решения, — все формулы в правой части, прямо или косвенно связанные с переменными решения, должны быть перенесены в левую часть с помощью алгебраических преобразований данного неравенства;

• не следует использовать в формулах модели линейного программирования нелинейные функции; такие функции могут использоваться в формулах рабочего листа, но только в том случае, если они не влияют (прямо или косвенно) на вычисление целевой функции;

• условия неотрицательности переменных решения не обязательно включать в табличную модель; как правило, они опускаются и указываются непосредственно в диалоговом окне средства «Поиск решения».

Одним из результатов выполнения этих рекомендаций является то, что все основные ко­эффициенты модели содержатся в отдельных ячейках, поэтому их легко изменять, не меняя формул модели. Кроме того, группирование переменных решения и ограничений позволяет копировать формулы для создания аналогичных формул. Благодаря группированию также упрощается работа с надстройкой «Поиск решения», поскольку для указания переменных реше­ния или ограничений можно использовать диапазоны ячеек рабочего листа.

Табличная модель, представленная на рис. 1.1, уже вполне пригодна для выполнения плановых расчетов. Для того чтобы удостовериться в правильности модели и получения хотя бы некоторого приемлемого решения, достаточно ввести в ячейки переменных решения (C6:E6) некоторые планируемые значения выпуска продукции. Допустим, что в очередном периоде планируется выпуск 8 тыс. ед. продукта A, 4 тыс. ед. продукта B и еще 2 тыс. ед. продукта C. Тогда форма рабочего листа электронной таблицы примет вид, представленный на рис. 1.2.

Рис. 1.2. Табличная модель с предварительными значениями

плановых показателей

Из модели на рис. 1.2 видно, что выпуск по предполагаемому плану может принести предприятию 748 тыс. руб. прибыли, то есть предлагаемый план вполне можно считать удовлетворительным. Однако предприятие при таком плане не способно полностью задействовать все имеющиеся у него дефицитные ресурсы, особенно это касается первого вида ресурса, для которого остаются нераспределенными более 10% запасов. И вполне очевидно, что возможно существование более оптимальных решений для рассматриваемой задачи.

Важно отметить одно обстоятельство, которое в дальнейшем будет постоянно учитываться при решении задачи оптимизации производственной программы – это целочисленное представление искомых плановых показателей. Целочисленность решения означает в экономическом смысле любую неделимость производственных объемов продукции и действующих факторов производства. Это условие не ограничивает возможности применения методов линейного программирования в серийном и массовом производстве. Выпускаемые объемы продукции при этих типах производства так велики, что округление нецелочисленного результата решения может лишь незначительно изменить оптимальное его значение. При количественном определении ресурсов использование средств производства и рабочей силы может изменяться в любых делимых единицах времени. Неделимость величин, описывающих применяемые материалы, устраняется путем округления значений решения.

На предприятиях с мелкосерийном или единичным производством использование методов линейного программирования при планировании производственной программы возможно лишь условно. Округление результата может привести к значительным изменениям значения оптимального решения. В этом случае целесообразно применение специальных методов целочисленного линейного программирования. И хотя рассматриваемый пример следует отнести к среднесерийному производству условие, получения целочисленного результата будет соблюдаться.

Для того чтобы не затрачивать время на попытки вручную, меняя значения переменных решения, найти наиболее выгодные плановые показатели можно, прибегнув к помощи ранее упомянутой надстройки табличного процессора Excel «Поиск решения».

Вызвав окно надстройки «Поиск решения», необходимо заполнить ее поля согласно примеру на рис. 1.3, при этом следует исходить из следующих положений.

Рис. 1.3. Заполнение полей надстройки «Поиск решения» для оптимизации модели краткосрочной производственной программы

Во-первых, необходимо определить целевую ячейку для оптимизации, которая соответствует значению целевой функции в задаче линейного программирования. В нашем примере это ячейка G18. Возможно использование абсолютных адресов ячеек и диапазонов с помощью специального символа ‘$’, что и происходит автоматически при их выборе с помощью курсора мыши. Целевую ячейку необходимо устанавливать равной максимальному значению – для этого в надстройке «Поиск решения» есть специальный флаг.

Во-вторых, результатом работы оптимизационной процедуры должно стать изменение плановых показателей выпуска, поэтому в качестве изменяемых ячеек устанавливаем диапазон C16:E16.

В-третьих, в качестве налагаемых ограничений, согласно рассматриваемой модели, последовательно добавляем условие целочисленности для искомых плановых показателей, находящихся в диапазоне C16:E16, а также условия неотрицательности, как для ранее указанных ячеек плана выпуска, так и для диапазона G21:G22. В последнем условии задается необходимость выполнения ограничений по использованию дефицитных ресурсов производства таким образом, чтобы их остаток после выполнения процедуры оптимизации был бы не меньше нуля.

Для того чтобы учесть линейный характер рассматриваемой модели, можно использовать дополнительные свойства оптимизационного алгоритма надстройки «Поиск решения», окно которых открывается по кнопке «Параметры». Для нашего примера имеет смысл установить флаги «Линейная модель» и «Неотрицательные значения». При установке последнего можно отказаться от ранее заданного условия неотрицательности целевых ячеек модели. Диалоговое окно дополнительных параметров надстройки «Поиск решения» представлено на рис. 1.4.

Среди других полей дополнительных параметров надстройки «Поиск решений» можно также использовать «Автоматическое масштабирование» для случая задач, в которых значения различных параметров отличаются друг от друга по абсолютной величине на несколько порядков. В случае моделей с большим количеством ограничений, как правило, исчисляемым несколькими десятками, следует увеличить максимальное время и предельное число итераций оптимизационного алгоритма и снизить при этом параметры точности решения. Остальные поля мало значимы для оптимизации задач линейного программирования.

Важно отметить, что для случаев с установлением различных флагов и значений дополнительных параметров, а также их комбинаций с явно заданными ограничениями надстройка «Поиск решения» может выдавать немного различающиеся результаты, что обусловлено, прежде всего, внутренним алгоритмом ее работы. Поэтому для задач оптимизации большой размерности имеет смысл использовать несколько различных вариантов задания ограничений и дополнительных параметров для получения наиболее приемлемого результата.

Рис. 1.4. Заполнение дополнительных параметров

надстройки «Поиск решения»

Диалоговое окно «Результаты поиска решения» сообщает о завершении поиска (рис. 1.5). То, что алгоритм «Поиск решения» завершил работу, не означает, что обязательно найдено оптимальное решение. Если получено сообщение об успешном завершении поиска, как на рис. 1.5, можно или сохранить найденное решение, выбрав соответствующую опцию, или отказаться от него, выбрав опцию «Восстановить исходные значения», в результате ячейкам переменных ре­шения будут возвращены значения, которые в них находились до запуска алгоритма «Поиска решения».

Если оптимальное решение найдено, в диалоговом окне «Результаты поиска решения» должно присутствовать два ключевых предложения:

1. Решение найдено.

2. Все ограничения и условия оптимальности выполнены.

Если хотя бы одного из этих предложений нет, то это означает, что программе не удалось оптимизировать модель. В этом случае надо проверить как математическую модель решаемой задачи, так и ее табличное представление, а также правильность задания параметров надстройки «Поиск решения».

Рис. 1.5. Диалоговое окно «Результаты поиска решений»

в случае успешного решения задачи оптимизации

Существует возможность также получить отчеты о решении трех типов, каждый из которых выводится на новый лист рабочей книги. Причем для задач линейного типа актуален только отчет «Результаты», фрагмент которого для рассматриваемого примера представлен на рис. 1.6.

Рис. 1.6. Отчет о результатах поиска оптимального решения

Приняв полученные надстройкой «Поиск решения», получим вид листа рабочей книги с оптимальной по прибыли краткосрочной производственной программой, представленный на рис. 1.7.

Рис. 1.7. Результаты оптимизации краткосрочной

производственной программы

Из данных рис. 1.7 видно, что получено решение задачи линейного программирования, которое, во-первых, позволило полностью задействовать все имеющиеся на предприятии лимитируемые ресурсы (остатки в ячейках G21:G22 обнулены), а во-вторых, увеличить до 824130 руб. ожидаемое значение прибыли на планируемый период.

Среди прочих из решения задачи можно сделать также вывод о приоритетности для принятых нами условий задачи производства продукта B. Причиной этого выступает совпадение для этого вида продукции достаточно высокого показателя относительной маржинальной прибыли с экономичными, по сравнению с другими продуктами, потребностями в дефицитных ресурсах. Причем преимущество над другими видами продукции достигается именно за счет эффективного соотношения названных факторов, а не просто из-за их самых низких значений, как для случая с продуктом A.

Основываясь на предыдущем замечании, следует отметить необходимость в практической деятельности нахождения не только оптимального значения модели, но и определения ее чувствительности к изменению исходных данных. Это утверждение можно проиллюстрировать следующим примером, в котором снизим переменные затраты, приходящееся на продукт C всего на 1 рубль (до 241), что в относительном выражении составляет около 0,4 %. Однако при таком незначительном изменении, например, закупочных цен или транспортных издержек результат оптимизации производственной программы может серьезно измениться, что хорошо видно на рис. 1.8.

Рис. 1.8. Результаты оптимизации краткосрочной производственной программы с учетом снижения переменных затрат на продукт C

Получаемое решение лишь номинально оставляет возможность производства продукта A (всего одной единицы), что определяется только необходимостью задействовать оставшиеся лимитируемые ресурсы. И при сохранении, опять-таки с разницей всего в одну единицу, плана выпуска продукции вида B остальная часть ресурсов может быть эффективно распределена на производство продукта C.

Возникновение подобных ситуаций, отличающихся высокой чувствительностью созданной модели, в практической деятельности требует применения специальных методов линейного и в целом математического программирования. В частности, для исследования влияния ограничивающих факторов модели может понадобиться решение двойственной задачи линейного программирования или применение более сложных методов параметрического программирования. Размерность, а значит, и сложность реальных задач может значительно возрастать из-за введения дополнительных ограничений, которые учитывают существующие особенности производства или сбыта продукции. Рассмотрению перечисленных проблем посвящен следующий раздел учебного пособия.