1.2. Аналогія формул поступального та обертального рухів (кінематика)

Поступальний рух (проекція на вісь Х)	Обертальний рух
Кінематичні характеристики
Формули рівномірного руху
Формули рівнозмінного руху

Основний закон динаміки поступального руху (другий закон Ньютона) виражається рівнянням:

де –імпульс тіла.

В класичній механіці (при малих швидкостях руху тіла) маса стала і рівняння приймає вигляд:

де прискорення

Сили в механіці:

а) сила гравітації: б) сила тяжіння:

в) сила пружності: г) сила тертя:

Закон збереження імпульсу:

Робота змінної сили при переміщенні описується формулою:

де проекція сили на напрямок переміщення, – довжина переміщення. Якщо незмінна сила напрямлена під кутом до переміщення:

Потужність визначається формулою:

Якщо потужність постійна:

Кінетична енергія поступального руху:

Потенціальна енергія взаємодії:

а) гравітації:

б) пружної деформації:

Основний закон динаміки обертального руху виражається рівнянням:

де – момент інерції тіла; – момент сили; – кутове прискорення.

Модуль моменту сили:

Напрямок моменту сили визначається за правилом свердлика.

Моменти інерції деяких фізичних тіл:

а) матеріальної точки

б) суцільного диску

в) стрижня відносно його середини

Модуль моменту імпульсу:

Проекція моменту імпульсу на ось Z:

Закон збереження моменту імпульсу:

Кінетична енергія тіла, що обертається навколо осі Z:

Таблиця 3

1.3. Аналогія формул поступального та обертального рухів (динаміка)

Поступальний рух	Обертальний рух
Основні динамічні характеристики
сила –	момент сили –
маса –	момент інерції –
імпульс тіла –	модуль моменту імпульсу:
Основний закон динаміки
Робота та енергія
Закони збереження

1.4. Приклади розв’язання задач

Приклад 1. Залежність пройденого шляху тіла від часу дається рівнянням де Знайти швидкість і

прискорення в момент часу

Розв’язання: Знайдемо швидкість тіла як похідну від шляху по часу:

Знайдемо прискорення тіла як похідну від швидкості по часу:

Приклад 2. Маховик у вигляді суцільного диску масою кг і радіусом см почав обертатися із сталим прискоренням під дією обертального моменту Знайти : 1) кутове прискорення; кінетичну енергію, яку набув маховик за час с від початку руху.

Розв’язання: З основного рівняння динаміки обертального руху знайдемо кутове прискорення:

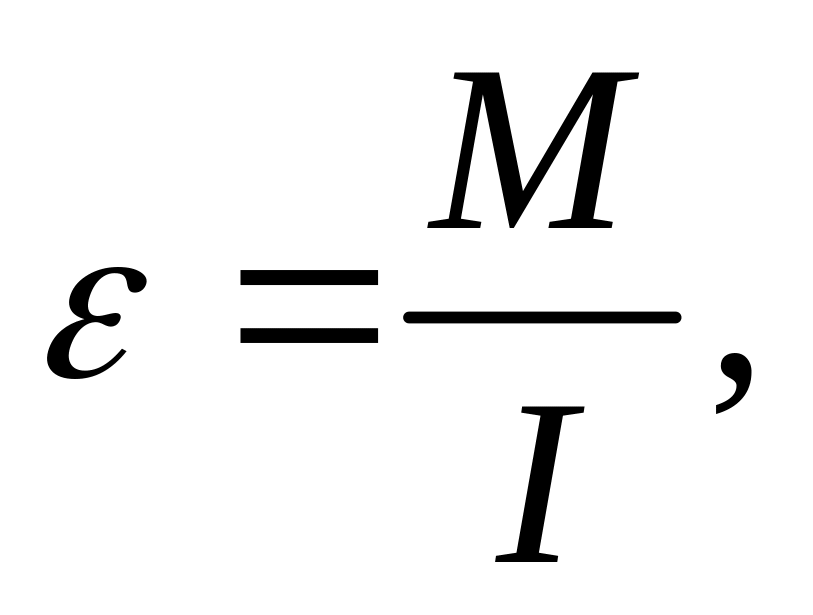
де – момент інерції маховика; – обертальний механічний момент.

Підставив момент інерції у вираз для кутового прискорення, отримаємо:

Підставимо значення величин у одиницях СІ:

Кінетичну енергію тіла, що обертається, отримаємо за формулою:

де ; кутова швидкість

Кінетична енергія маховика:

Підставимо значення величин у одиницях СІ:

Приклад 3. Рівняння коливань точки має вигляд (зміщення у сантиметрах, час у секундах). Знайти: 1) амплітуду, період коливань; 2) зміщення точки у момент часу 3) максимальну швидкість та максимальне прискорення.

Розв’язання: Запишемо рівняння гармонійних коливань:

Порівнюючи рівняння гармонійних коливань з рівнянням коливань точки, запишемо: см, , = 0.

Період коливань знайдемо за формулою:

Знайдемо зміщення в момент часу

Швидкість коливань знайдемо як першу похідну від зміщення:

Максимальне значення швидкості коливань при :

Прискорення знайдемо як першу похідну від швидкості:

Максимальне значення прискорення коливань при :