Задание 9

Определить минимально необходимый объём испытаний с целью оценки среднего квадратического отклонения, если α = 0,05 и Δ_σ = 0,6.

Подсчитываем левую часть уравнения (2.36)

(1 + Δ_σ)² = (1 + 0,6)² = 2,56

По таблице 2.10 для различных k = n – 1 вычисляем отношения χ²_0,05 и χ²_0,5, выбираем такое значение k = n – 1, при котором отношение указанных величин будет меньше или равняться значения левой части уравнения (2.35).

Для k = 1

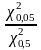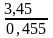= = 7,648352

Для k = 3

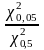= = 3,299578

Для k = 4

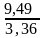= = 2,824405

Для k = 5

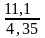= = 2,551724

Окончательно принимаем n = k + 1 = 6

При использовании формулы (2.36) получаем

n = 1,5 + 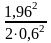= 6, 84

Если в результате испытаний планируется одновременная оценка и среднего значения, и среднего квадратического отклонения контролируемой характеристики с заданной точностью и надёжностью, то объём испытаний определяют как наибольшее из двух значений n, найденных по формулам (2.31) – (2.33) и (2.35) – (2.36).

Для этой цели могут быть также использованы таблицы 2.10 и 2.11.

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

Задание 1

По результатам примера 2.1 проверить нулевую гипотезу о принадлежности последнего образца вариационного ряда той же генеральной совокупности, как и остальные образцы.

= 404,75

s = 12,4606

u_n = 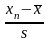= = 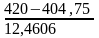1,223857.

u_n = 1,223857< u_α=2,44

Заключение: нулевая гипотеза не отклоняется, т.е. результат x₂₀ = 420 не является следствием грубой ошибки эксперимента.

Задание 2

По результатам испытания 18 образцов произведена оценка дисперсии s² = 126,9. Проверить нулевую гипотезу, заключающуюся в том, что выборка взята из генеральной совокупности с дисперсией σ²₀ = 100 против альтернативной σ² > σ²₀.

Вычисляем левую часть неравенства (3.3):

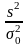= =1,269

Задаёмся α = 0,05 и по таблице 2.10 находим для k = n – 1 = 17

χ²_0,05 = 27,6

Вычисляем правую часть соотношения (3.3)

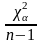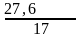= = 1,269

Заключение: неравенство (3.3) не выполняется, следовательно, применяют альтернативную гипотизу.

Задание 3

Определить минимальный объём выборки для проверки нулевой гипотезы о равенстве дисперсий с помощью двустороннего критерия (3.5), если α = 0,05; β = 0,07 и Δσ = 0,3

По таблице 2.8 находим z_1–β = z_0,9 = 1,282; z_1–α/2 = z_0,975 = 1,96.

На основании формулы (3.7) определяем

n = 1,5 + 0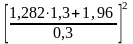,5 ≈ 75

Критерий равенства дисперсий двух генеральных совокупностей. Пусть по результатам испытаний двух независимых выборок объёмом n₁ и n₂ из нормально распределённых совокупностей подсчитаны оценки дисперсий, причём s²₁ > s²₂. Требуется проверить нулевую гипотезу о том, что указанные выборки принадлежат генеральным совокупностям с равными дисперсиями, т.е. σ²₁ = σ²₂ = σ² при альтернативной гипотезе σ²₁ ≠ σ²₂. С этой целью используют двусторонний F-критерий (критерий Фишера), для чего находят статистику

F = 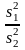при s²₁ > s²₂. (3.8)

И сопоставляют с критическим значением F_1–α/2, представленным в 3.3

Если

F = ≤ F_1–α/2, (3.9)

то гипотезу о равенстве дисперсий двух генеральных совокупностей, из которых взяты выборки, т.е. σ²₁ = σ²₂ = σ², не отклоняют.

В случае невыполнения неравенства (3.9) нулевую гипотезу отвергают.

При альтернативной гипотезе σ²₁ > σ²₂ используют односторонний критерий

F = ≤ F_1–α, (3.10)

если неравенство выполняется, то нулевую гипотезу не отвергают. В противном случае принимают σ²₁ > σ²₂.

В случае подтверждения нулевой гипотезы σ²₁ = σ²₂ = σ² по двум выборочным дисперсиям производят новую оценку генеральной дисперсии σ²:

s² =