
МИНОБРНАУКИ РОССИИ
Волжский политехнический институт (филиал)
федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Волгоградский государственный технический университет»
(ВПИ (филиал) ВолгГТУ)
Автомеханический факультет
Кафедра ВТО
Семестровая работа по дисциплине
«Метрология, стандартизация и сертификация»
Вариант № __
Выполнил студент
группы ВТС-321
Иванов И.И.
Проверил ст.преп.
Белухин Р.А.
Волжский 2014
ОЦЕНКА ЧИСЛОВЫХ ХАРАКТЕРИСТИК И ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Задание 1
Требуется
вычислить значения выборочных среднего
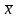 ,
медианы
,
медианы
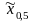 ,
дисперсии s2,
среднего квадратического отклонения
s
и коэффициента вариации ν ряда значений:
408, 404, 399, 412, 420, 418, 400, 413, 416, 417, 396, 409, 401, 395,
398, 370
,
дисперсии s2,
среднего квадратического отклонения
s
и коэффициента вариации ν ряда значений:
408, 404, 399, 412, 420, 418, 400, 413, 416, 417, 396, 409, 401, 395,
398, 370
i |
xi |
Предварительные расчёты:
Выборочное среднее значение (2.1):
=
Выборочная медиана (2.3):
=
Выборочная дисперсия (2.5):
s2
=
= 155,267. Смещённая оценка среднего квадратического отклонения (2.6):
s
=
Несмещённая оценка среднего квадратического отклонения (2.8) и таблица 2.1: s1 = 1,017 · 12,4606=12,6724. Выборочный коэффициент вариации (2.7):
ν
=
|
1 |
370 |
|
2 |
395 |
|
3 |
396 |
|
4 |
398 |
|
5 |
399 |
|
6 |
400 |
|
7 |
401 |
|
8 |
404 |
|
9 |
408 |
|
10 |
409 |
|
11 |
412 |
|
12 |
413 |
|
13 |
416 |
|
14 |
417 |
|
15 |
418 |
|
16 |
420 |
|
|
|
|
|
|
|
|
|
|
|
|
Выборочная медиана при нечётном объеме выборки n = 2m – 1 равна среднему члену вариационного ряда:
= xm,
(2.3)
Выборочная дисперсия
s2
=
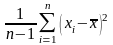 ,
(2.4)
,
(2.4)
или
s2 = . (2.5)
Выборочное среднее квадратическое отклонение и выборочный коэффициент вариации
s
=
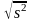 ,
(2.6)
,
(2.6)
ν
=
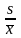 .
(2.7)
.
(2.7)
Вычисление выборочных моментов третьего и четвёртого порядков при объёме п < 50 нецелесообразно в связи с их большими вероятными отклонениями от генеральных моментов.
Задание 2
Вычислить значения статистик, указанных в примере 2.1, и выборочные значения показателей асимметрии и эксцесса для случайной величины x = lgN. Ряд значений N, Производим логарифмирование и формируем вариационный ряд:
i |
N |
xi = lgN |
i |
N |
xi = lgN |
i |
N |
xi = lgN |
i |
N |
xi = lgN |
1 |
74133,6 |
4,8700 |
21 |
161631 |
5,2085 |
41 |
290932 |
5,4638 |
61 |
391011 |
5,5922 |
2 |
83019,5 |
4,9192 |
22 |
162711 |
5,2114 |
42 |
292004 |
5,4654 |
62 |
394714 |
5,5963 |
3 |
105629 |
5,0238 |
23 |
170237 |
5,2311 |
43 |
295922 |
5,4712 |
63 |
407535 |
5,6102 |
4 |
109824 |
5,0407 |
24 |
182835 |
5,2621 |
44 |
296535 |
5,4721 |
64 |
444240 |
5,6476 |
5 |
110836 |
5,0447 |
25 |
205410 |
5,3126 |
45 |
305459 |
5,4850 |
65 |
444547 |
5,6479 |
6 |
111319 |
5,0466 |
26 |
214819 |
5,3321 |
46 |
314942 |
5,4982 |
66 |
472484 |
5,6744 |
7 |
116541 |
5,0665 |
27 |
234306 |
5,3698 |
47 |
315594 |
5,4991 |
67 |
656524 |
5,8173 |
8 |
120728 |
5,0818 |
28 |
237449 |
5,3756 |
48 |
330063 |
5,5186 |
68 |
733185 |
5,8652 |
9 |
121339 |
5,0840 |
29 |
241021 |
5,3821 |
49 |
331737 |
5,5208 |
69 |
744747 |
5,8720 |
10 |
128232 |
5,1080 |
30 |
242020 |
5,3839 |
50 |
332730 |
5,5221 |
70 |
790662 |
5,8980 |
11 |
128822 |
5,1100 |
31 |
242577 |
5,3848 |
51 |
333496 |
5,5231 |
71 |
804241 |
5,9054 |
12 |
131840 |
5,1200 |
32 |
247020 |
5,3927 |
52 |
349750 |
5,5438 |
72 |
815046 |
5,9112 |
13 |
131931 |
5,1203 |
33 |
249817 |
5,3976 |
53 |
352414 |
5,5471 |
73 |
830189 |
5,9192 |
14 |
133514 |
5,1255 |
34 |
256153 |
5,4085 |
54 |
361773 |
5,5584 |
74 |
851472 |
5,9302 |
15 |
145240 |
5,1621 |
35 |
256742 |
5,4095 |
55 |
363858 |
5,5609 |
75 |
901063 |
5,9548 |
16 |
147930 |
5,1701 |
36 |
257214 |
5,4103 |
56 |
364193 |
5,5613 |
76 |
1209456 |
6,0826 |
17 |
150015 |
5,1761 |
37 |
264527 |
5,4225 |
57 |
368150 |
5,5660 |
77 |
1473520 |
6,1684 |
18 |
151921 |
5,1816 |
38 |
271424 |
5,4336 |
58 |
368235 |
5,5661 |
78 |
1821488 |
6,2604 |
19 |
155126 |
5,1907 |
39 |
272299 |
5,4350 |
59 |
380107 |
5,5799 |
79 |
1895053 |
6,2776 |
20 |
157241 |
5,1966 |
40 |
290264 |
5,4628 |
60 |
382738 |
5,5829 |
80 |
2875279 |
6,4587 |
Определяем размах варьирования логарифма:
R = 6,458679992– 4,87001509= 1,5886649.
Размах разбиваем на равные интервалы.
Δx
≈
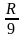 =
=
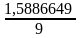 = 0,1765183
= 0,1765183
За длину интервала принимаем Δx = 0,18
Таблица 2.3
e |
Границы интервала |
Середина интервала xj |
Число наблюдений nj |
|
1 |
4,870 |
5,050 |
4,96 |
6 |
2 |
5,050 |
5,230 |
5,14 |
16 |
3 |
5,230 |
5,410 |
5,32 |
13 |
4 |
5,410 |
5,590 |
5,50 |
25 |
5 |
5,590 |
5,770 |
5,68 |
6 |
6 |
5,770 |
5,950 |
5,86 |
8 |
7 |
5,950 |
6,130 |
6,04 |
2 |
8 |
6,130 |
6,310 |
6,22 |
3 |
9 |
6,310 |
6,490 |
6,40 |
1 |
Предварительные расчёты:
![]() =
436,8;
=
436,8;
 = 2393;
= 2393;
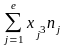 =
13156;
=
13156;
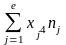 = 72599.
= 72599.
Выборочное среднее значение (2.10):
=
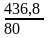 = 5,4595.
= 5,4595.
Выборочная медиана (2.3):
= (5,4627+ 5,4638) = 5,4633.
Выборочная дисперсия (2.12):
s2
=
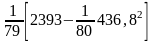 = 0,1050.
= 0,1050.
Выборочное среднее и выборочный коэффициент вариации (2.6) и (2.7):
s
=
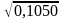 = 0,3240;
ν
=
= 0,3240;
ν
=
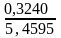 = 0,0593.
= 0,0593.
Для вычисления выборочных показателей ассиметрии и эксцесса по формулам (2.13) определяем оценки начальных моментов первых четырёх порядков:
h1 = 5,4560; h2 = 29,91;
h3 = 164,45; h4 = 907,49.
и по формулам (2.14) – оценки центральных моментов третьего и четвёртого порядка
m3 = 0,0227;
m4 = 0,0347.
Выборочные показатели ассиметрии и эксцесса
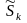 =
=
 = 0,6680722;
= 0,6680722;
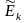 =
=
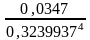 –3 = 0,1516.
–3 = 0,1516.

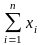 =
6476;
=
6476;
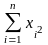 = 2623490.
= 2623490.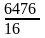 = 404,75.
= 404,75.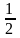 (404+
408) = 406.
(404+
408) = 406.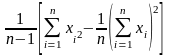 =
=
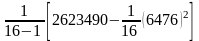 =
=
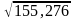 = 12,4606.
= 12,4606.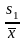 =
=
 = 0,03131.
= 0,03131.