8.3. Потенциальная энергия при кручении

Потенциальная энергия, накопленная в элементе вала длиной dz, численно равна работе моментов М_к, приложенных к торцам данного элемента. Предполагая прямую пропорциональную зависимость между крутящим моментом и углом закручивания, получим выражение для элементарной потенциальной энергии (с учетом формулы (8.10))

. (8.12)

Интегрируя выражение (8.12) по длине вала, получим выражение для потенциальной энергии деформации

. (8.13)

Если М_кр=const и GJ_p=const по длине вала, то получим

(8.14)

8.4. Кручение бруса некруглого поперечного сечения

В инженерной практике довольно часто кручению подвергается брус некруглого поперечного сечения - прямоугольного, эллиптического и др. В этом случае гипотеза плоских сечений неприменима, так как сечения депланируют (искажаются, искривляются). Данная задача решается методами теории упругости. Однако некоторые важные закономерности можно получить на основе закона парности касательных напряжений. Следует особо подчеркнуть, что на свободной внешней поверхности бруса не могут действовать никакие внутренние усилия (напряжения), т.к. на точки такой поверхности не наложено ограничений на свободу перемещения.

Если учесть указанную особенность свободной поверхности, то можно определить направление касательных напряжений в точке А произвольного контура. Пусть в точке А (рис. 8.6а) действуют произвольно направленные касательные напряжения τ. Разложим напряжения на составляющие: направленные по касательной к контуру в точке А – τ₁ и перпендикулярно касательной – τ₂. По закону парности касательных напряжений на свободной поверхности бруса должны действовать касательные напряжения τ₂^', но это невозможно, т.к. на свободной поверхности напряжения равны нулю. Вывод: касательные напряжения при кручении бруса произвольного сечения в каждой точке внешнего контура направлены по касательной к контуру в данной точке.

Рис. 8.6. Касательные напряжения на контуре

Аналогично можно доказать, что в угловых точках прямоугольных сечений бруса (рис. 8.6б) касательные напряжения должны равнять нулю.

Расчетные формулы для касательных напряжений и углов закручивания бруса произвольного сечения приводят к виду:

, , (8.15)

где  - момент сопротивления кручению,  - момент инерции при кручении, которые являются геометрическими характеристиками сечения и приводятся в справочниках (крутильная характеристика сечения).

Так, например, для эллиптического сечения (рис. 8.7) касательные напряжения в точках А и В (a, b – полуоси эллипса)

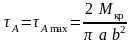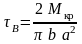, , (8.16)

а угол закручивания для участка однородного бруса длиной l

.

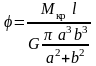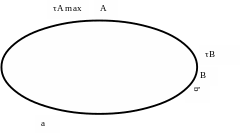
Рис. 8.7. Распределение касательных напряжений при кручении бруса эллиптического сечения

У бруса прямоугольного сечения (рис. 8.8) максимальные касательные напряжения при кручении действуют в середине больших сторон (точка А). Они определяются соотношением

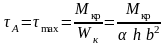(8.17)

В середине меньших сторон прямоугольника напряжения равны

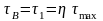. (8.18)

Угловые перемещения вычисляются по формуле

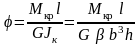. (8.19)

Рис. 8.8. Касательные напряжения в брусе прямоугольного сечения

Коэффициенты α, β, η зависят от соотношения сторон прямоугольника и приводятся в справочной литературе.