4 .3.2 Методика синтеза системы управления в базисе элементарных логических элементов и-не или или-не

Рассмотрим методику синтеза системы управления в базисе элементарных логических элементов на конкретном примере минимизации переключательных функций с помощью диаграмм Вейча.

Пусть задана переключательная функция четырех аргументов, которая равна 1 на 0, 1, 2, 4, 8, 10, 11, 12, 14, 15 наборах. Необходимо составить и минимизировать данную переключательную функцию с помощью диаграмм Вейча. Решение этой задачи проведем в следующем порядке.

1. По заданному набору переключательной функции составим таблицу истинности.

Таблица 3 – Таблица истинности заданной переключательной функции

i	x4	x3	x2	x1	y
0	0	0	0	0	1
1	0	0	0	1	1
2	0	0	1	0	1
3	0	0	1	1	0
4	0	1	0	0	1
5	0	1	0	1	0
6	0	1	1	0	0
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	0
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	0
14	1	1	1	0	1
15	1	1	1	1	1

2. По полученной таблице истинности составим совершенную дизъюнктивную нормальную форму (СДНФ) переключательной функции:

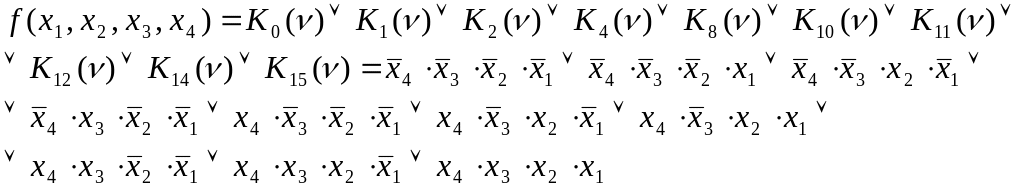(9)

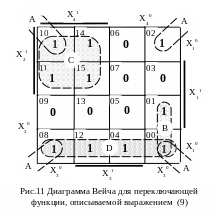
3. П остроим диаграмму Вейча данной переключательной функции. В верхнем левом углу каждой клетки диаграммы Вейча запишем номер клетки i. Согласно таблице истинности заполним каждую клетку диаграммы Вейча единицами и нулями (рис.11).

4. Выделим на диаграмме Вейча 1-кубы максимального размера. Таких куба четыре: куб А – клетки с номерами 0,2,8,10; куб В – клетки с номерами 0,1; куб С – клетки с номерами 10,11,14,15; куб D – клетки с номерами 0,4,8,12.

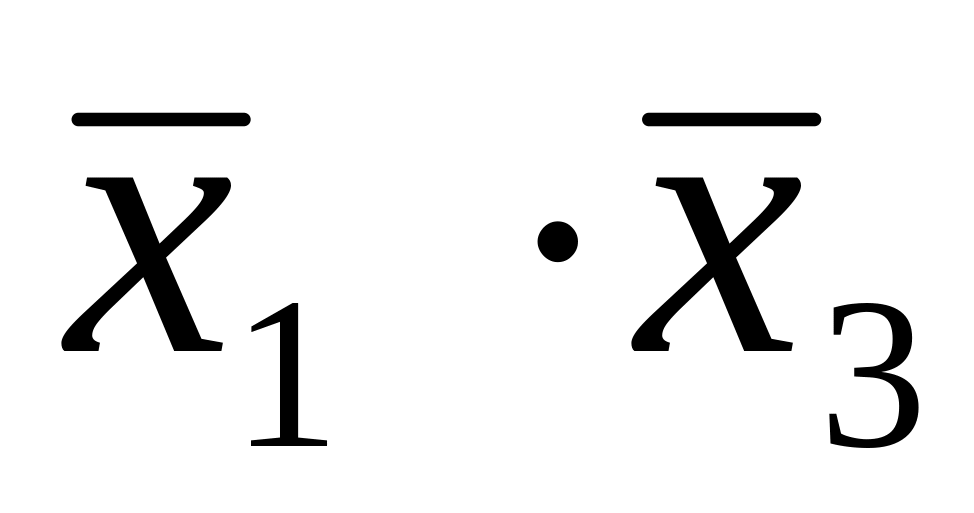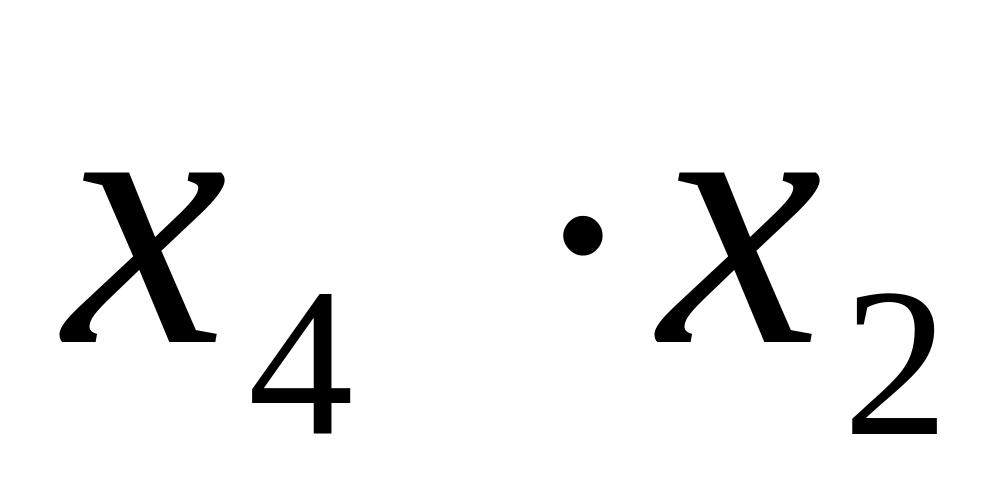5. Кубу А соответствует контерм , поскольку он находится на пересечении Х₃⁰ и Х₁⁰. Кубу В соответствует контерм , поскольку он находится на пересечении Х₄⁰, Х₃⁰ и Х₂⁰. Кубу С соответствует контерм , поскольку он находится на пересечении Х₄¹ и Х₂¹. Кубу D соответствует контерм , поскольку он находится на пересечении Х₂⁰ и Х₁⁰.

При затруднении при определении контерм можно воспользоваться следующим методом. Например, для куба А выпишем в столбик номера всех клеток, которые занимает куб в двоичном виде:

х4	х3	х2	х1	Номер клетки
0	0	0	0	00
0	0	1	0	02
1	0	0	0	08
1	0	1	0	10

Как видно колонки х₃ и х₁ имеют одинаковое значение, равное 0, что противоположно 1 кубу, поэтому контерм куба А равен .

Для куба С аналогічно получим:

х4	х3	х2	х1	Номер клетки
1	0	1	0	10
1	0	1	1	11
1	1	1	0	14
1	1	1	1	15

Как видно колонки х₄ и х₂ имеют одинаковое значение, равное 1, что соответствует 1 кубу, поэтому контерм куба С равен .

6. Тогда минимизированная дизъюнктивная нормальная форма (МДНФ) данной переключательной функции:

(10)

Для схемной реализации соответствующей логической функции в смешанном базисе необходимо использовать один четырехвходовый элемент ИЛИ, два двухвходовых элемента И, один трехвходовый элемент И и четыре элемента НЕ.

7. Для получения минимизированной нормальной формы (МНФ) переключательной функции в едином базисе И-НЕ, необходимо использовать следующее соотношение:

(11)

Тогда преобразуя МДНФ переключательной функции, описываемой выражением (10), с помощью выражения (11), можно получить МНФ в базисе И-НЕ:

(12)

Для схемной реализации такой функции необходимо использовать девять элементов И-НЕ (рис.12).

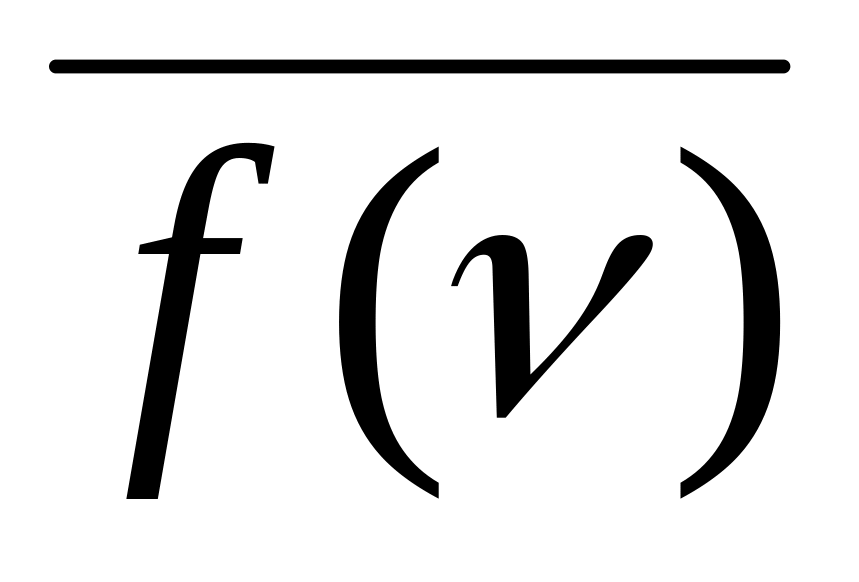8. Д ля получения МНФ в базисе ИЛИ-НЕ необходимо после нахождения МДНФ (см.п.6) преобразовать ее в минимизированную конъюнктивную нормальную форму (МКНФ) для чего надо найти МДНФ инверсной функции , т.е. найти минимальное покрытие всех 0-клеток функции . Для нахождения МКНФ переключательной функции необходимо воспользоваться законом двойственности, установленного Шенноном:

, (13)

согласно которому инверсию любой функции можно получить взаимной заменой переменных х_р и их инверсией и операций дизъюнкции и конъюнкции.

Для нашего примера после преобразования МДНФ переключательной функции (10) с помощью выражения (13) получим МКНФ данной переключательной функции:

(14)

9. Для получения минимизированной нормальной формы (МНФ) переключательной функции в едином базисе ИЛИ-НЕ, необходимо использовать следующее соотношение:

(15)

Тогда преобразуя МКНФ переключательной функции, описываемой выражением (14), с помощью выражения (15), можно получить МНФ в базисе ИЛИ-НЕ:

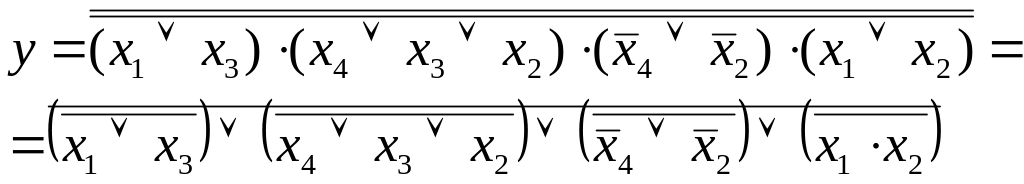(16)

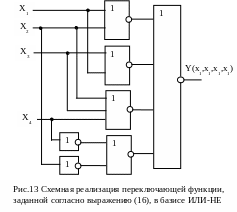Д ля схемной реализации такой функции необходимо использовать семь элементов ИЛИ-НЕ (рис.13).