Оценка автокорреляции уровней временного ряда

Лаг	Коэффициент автокорреляции
1	0,210604
2	-0,487516
3	0,159098
4	0,977109
5	0,149058
6	-0,684806
7	0,042431
8	0,975826

По графику исходного ряда (см. рис. 2.1) и значениям коэффи­циента автокорреляции (см. табл. 2.2) можно установить наличие приблизительно равной амплитуды колебаний. Это свидетельствует о возможном существовании аддитивной модели. Рассчитаем ее ком­поненты.

Шаг 1. Проведем выравнивание исходных уровней временного ряда методом скользящей средней: просуммируем уровни ряда по­следовательно за каждые четыре квартала со сдвигом на один период и определим значения условного годового объема потребления элек­троэнергии; разделив полученные суммы на четыре, найдем сколь­зящие средние. Отметим, что полученные таким образом выровнен­ные значения уже не содержат сезонной компоненты. Приведем эти значения в соответствие с фактическими периодами времени, для чего найдем средние значения из двух последовательных скользящих средних — центрированные скользящие средние.

Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями временного ряда и центрированными скользящими средними. Используем эти оценки для расчета значе­ний сезонной компоненты S. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты S_i. В моделях с сезонной компонентой обычно предполагается, что сезонные воз­действия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого: 1.1. Найдем скользящие средние (графа 3 табл.2.3). Полученные таким образом выровненные значения уже не содержат сезонной компоненты. 1.2. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (графа 4 табл.2.3).

Таблица 2.3

t	yt	Скользящая средняя	Центрированная скользящая средняя	Оценка сезонной компоненты
1	30,6	-	-	-
2	22,44	31,11	-	-
3	25,5	32,64	31,875	-6,375
4	45,9	33,15	32,895	13,005
5	36,72	34,425	33,7875	2,9325
6	24,48	35,7	35,0625	-10,5825
7	30,6	36,72	36,21	-5,61
8	51	37,74	37,23	13,77
9	40,8	38,602	38,171	2,629
10	28,56	40,482	39,542	-10,982
11	34,048	42,252	41,367	-7,319
12	58,52	43,89	43,071	15,449
13	47,88	44,688	44,289	3,591
14	35,112	44,422	44,555	-9,443
15	37,24		-	-
16	57,456		-	-

2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (графа 5 табл.2.3). Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты S_i. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

Таблица 2.4

Показатели	1	2	3	4
1	-	-	-6,375	13,005
2	2,9325	-10,5825	-5,61	13,77
3	2,629	-10,982	-7,319	15,449
4	3,591	-9,443	-	-
Всего за период	9,1525	-31,0075	-19,304	42,224
Средняя оценка сезонной компоненты	3,050833333	-10,33583333	-6,434666667	14,07466667
Скорректированная сезонная компонента, Si	2,962083333	-10,42458333	-6,523416667	13,98591667

Для данной модели имеем:

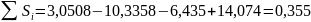
Определим корректирующий коэффициент: k = 0,355/4 = 0,08875. Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффици­ентом k:

;

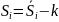S₁ = – 0,08875= 2,962083333;

S₂ = - – 0,08875= -10,42458333;

S₃ = - – 0,08875= -6,523416667;

S₄ = 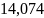– 0,08875= 13,98591667.

Занесем в таблицу скорректированные сезонные компоненты. Проверим условие равенства нулю суммы значений сезонной компоненты:

.

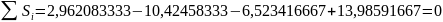Занесем полученные значения в таблицу 2.5 для соответствующих кварталов каждого года (графа 3).

Шаг 3. Элиминируем влияние сезонной компоненты, вычитая ее значение из значения каждого уровня исходного временного ряда. Получим величины Т + Е = Y – S (см. табл. 2.5, графа 4). Эти значения рассчитываются за каждый период и содержат только тенденцию и случайную компоненту.

Таблица 2.5

t	Yt	Si	T+E= Yt-Si	T	T + S	E= Yt-(T+S)	E2
1	2	3	4	5	6	7	8
1	30,6	2,962083333	27,63791667	29,6013	32,56338333	-1,963383333	3,854874114
2	22,44	-10,42458333	32,86458333	30,7116	20,28701667	2,152983333	4,635337234
3	25,5	-6,523416667	32,02341667	31,8219	25,29848333	0,201516667	0,040608967
4	45,9	13,98591667	31,91408333	32,9322	46,91811667	-1,018116667	1,036561547
5	36,72	2,962083333	33,75791667	34,0425	37,00458333	-0,284583333	0,080987674
6	24,48	-10,42458333	34,90458333	35,1528	24,72821667	-0,248216667	0,061611514
7	30,6	-6,523416667	37,12341667	36,2631	29,73968333	0,860316667	0,740144767
8	51	13,98591667	37,01408333	37,3734	51,35931667	-0,359316667	0,129108467
9	40,8	2,962083333	37,83791667	38,4837	41,44578333	-0,645783333	0,417036114
10	28,56	-10,42458333	38,98458333	39,594	29,16941667	-0,609416667	0,371388674
11	34,048	-6,523416667	40,57141667	40,7043	34,18088333	-0,132883333	0,01765798
12	58,52	13,98591667	44,53408333	41,8146	55,80051667	2,719483333	7,3955896
13	47,88	2,962083333	44,91791667	42,9249	45,88698333	1,993016667	3,972115434
14	35,112	-10,42458333	45,53658333	44,0352	33,61061667	1,501383333	2,254151914
15	37,24	-6,523416667	43,76341667	45,1455	38,62208333	-1,382083333	1,91015434
16	57,456	13,98591667	43,47008333	46,2558	60,24171667	-2,785716667	7,760217347
							34,678

Шаг 4. Определим компоненту T данной модели. Для этого про­ведем аналитическое выравнивание ряда (Т + Е) с помощью линейного тренда. Результаты аналитического выравнивания:

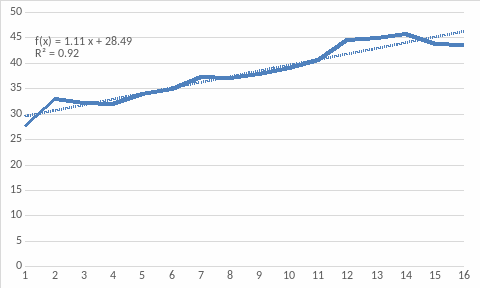
Т =1,1103x + 28,491.

Подставляя в это уравнение значения t=1,...,16, найдем уровни Т для каждого периода (см. табл. 2.5, графа 5).

Шаг 5. Найдем значения уровней временного ряда, полученные по аддитивной модели. Для этого прибавим к уровням Т значения сезонной компоненты для соответствующих кварталов.

Шаг 6. В соответствии с методикой построения аддитивной моде­ли расчет ошибки производится по формуле Е=Y—(T+S). Числен­ные значения абсолютных ошибок приведены в графе 7 таблице 2.5. По аналогии с моделью регрессии для оценки качества построения мо­дели или для выбора наилучшей модели можно применять сумму квадратов полученных абсолютных ошибок. Для данной аддитивной модели сумма квадратов абсолютных ошибок равна 34,678. По отно­шению к общей сумме квадратов отклонений уровней временного ряда от значения его среднего уровня (y-y_cp)², равного 1942,351388, эта величина составляет чуть более 1%:

(1 – 34,678/1942,351388) ∙ 100= 98,2.

Следовательно, аддитивная модель объясняет 98,2% общей вари­ации уровней временного ряда за 16 кварталов.

Y	Y cр	Y-Y ср	(Y-Y ср)²
30,6	37,9285	-7,3285	53,70691225
22,44	37,9285	-15,4885	239,8936323
25,5	37,9285	-12,4285	154,4676123
45,9	37,9285	7,9715	63,54481225
36,72	37,9285	-1,2085	1,46047225
24,48	37,9285	-13,4485	180,8621523
30,6	37,9285	-7,3285	53,70691225
51	37,9285	13,0715	170,8641123
40,8	37,9285	2,8715	8,24551225
28,56	37,9285	-9,3685	87,76879225
34,048	37,9285	-3,8805	15,05828025
58,52	37,9285	20,5915	424,0098723
47,88	37,9285	9,9515	99,03235225
35,112	37,9285	-2,8165	7,93267225
37,24	37,9285	-0,6885	0,47403225
57,456	37,9285	19,5275	381,3232563
			1942,351388