1.3 Метод «огибающих кривых»

Прогнозирование на основе временных рядов состоит в том, что на основе историко-фактических данных строят кривую роста того или иного показателя, характеризующего развитие технической системы, и пытаются продолжать эту кривую «в будущее». Этот метод в сравнительно большей степени основан на фактических, объективных данных.

Метод огибающих кривых можно использовать в разработке целевых комплексных программ (ЦКП). Состояние ЦКП определяется множеством характеристику 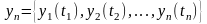которые изменяются во времени. Из этого множества характеристик выбираются такие, которые являются наиболее важными, определяющими состояние и развитие ЦКП: 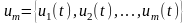Количество основных характеристик следует выбирать как можно меньше для того, чтобы создать условия для глубокого и всестороннего анализа. При прогнозировании используется ряд временных состояний выделенных основных характеристик ЦКП. Прогнозирование параметра 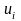осуществляется путем подстановки времени прогноза t_пр , в прогнозную модель

.

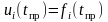Особое место при прогнозировании на основе огибающих кривых занимает теоретический, качественный анализ целевых комплексных программ. Выбор формы огибающей кривой затрудняется тем, что ее форма зависит от изменения основных характеристик, одни из которых развиваются плавно, эволюционно, скачкообразно, революционно.

Данные периода наблюдения

Таблица 1.1

Показатель	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005
Yфакт	141,780	140,250	139,740	140,250	139,740	139,740	125,460	121,890	120,870	119,850
Показатель	2006	2007	2008	2009	2010	2011	2012	2013	2014	2015
Yфакт	118,636	114,912	112,784	106,400	106,400	104,804	98,420	96,292	89,908	88,844

По данным таблицы построим график значений и добавим линию тренда с помощью программного продукта Microsoft Excel в виде линейной, логарифмической, степенной, экспоненциальной и полиномиальной функций. Для примера рассмотрим построение логарифмической линии тренда (рис.1.1). Результаты и полученные данные объединим в таблицу для выбора наиболее предпочтительной модели (таблица 1.2).

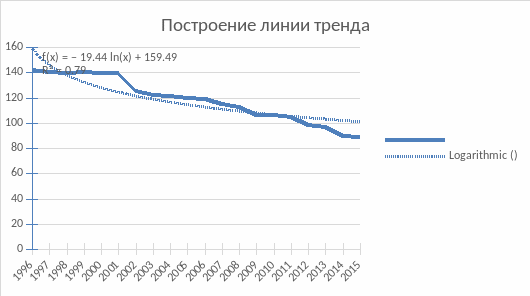
Рис. 1.1.

Аппроксимирующая функция

Таблица 1.2

Модель тренда	Математическое представление модели		σ
Логарифмическая	y = -19,44ln(x) + 159,49	0,7864	8,23

Так же рассчитаем стандартное отклонение σ. Расчет произведем по формуле:

σ = ;

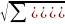где 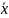– среднее значение, а n – размер выборки.

Если определяем отклонение не от среднего, а от линии тренда, то в этой формуле вместо   следует использовать значения точек линии тренда (на основании полученного уравнения).

Используя данную модель, рассчитаем точечные интервальные прогнозы:

y21 = -19,44ln(21) + 159,49= 100,3044838;

y22 = -19,44ln(22) + 159,49= 99,40013471.

Рассчитываем величины интервалов:

;

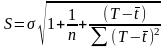Так же рассчитаем стандартное отклонение σ. Расчет произведем по формуле:

σ = ;

где – среднее значение, а n – размер выборки.

1) (x-̄x)²= (141,780-(-19,44ln(1) + 159,49)^2= 313,6441

2) (x-̄x)²= (140,250-(-19,44ln(2) + 159,49))^2=33,23774793

3) (x-̄x)²= (139,740-(-19,44ln(3) + 159,49))^2= 2,582522574

4) (x-̄x)²= (140,250-(-19,44ln(4) + 159,49))^2=59,43735209

5) (x-̄x)²= (139,740-(-19,44ln(5) + 159,49))^2= 133,1132836

6) (x-̄x)²= (139,740-(-19,44ln(6) + 159,49))^2=227,4608144

7) (x-̄x)²= (125,460-(-19,44ln(7) + 159,49))^2= 14,42855133

8) (x-̄x)²= (121,890-(-19,44ln(8) + 159,49))^2=7,976916603

9) (x-̄x)²= (120,870-(-19,44ln(9) + 159,49))^2=16,76121088

10) (x-̄x)²= (119,850-(-19,44ln(10) + 159,49))^2=26,23748817

11) (x-̄x)²= (118,636-(-19,44ln(11) + 159,49))^2= 33,19009004

12) (x-̄x)²= (114,912-(-19,44ln(12) + 159,49))^2=13,90234813

13) (x-̄x)²= (112,784-(-19,44ln(13) + 159,49))^2= 9,964221472

14) (x-̄x)²= (106,400-(-19,44ln(14) + 159,49))^2=3,192388056

15) (x-̄x)²= (106,400-(-19,44ln(15) + 159,49))^2=0,198473895

16) (x-̄x)²= (104,804-(-19,44ln(16) + 159,49))^2= 0,619172643

17) (x-̄x)²= (98,420-(-19,44ln(17) + 159,49))^2=35,90804989

18) (x-̄x)²= (96,292-(-19,44ln(18) + 159,49))^2=49,12850652

19) (x-̄x)²= (89,908-(-19,44ln(19) + 159,49))^2= 152,3275866

20) (x-̄x)²= (88,844-(-19,44ln(20) + 159,49))^2=153,9824025

Далее суммируем полученные показатели:

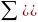
σ = =

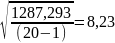
Рассчитываем величины интервалов:

;

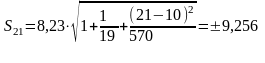(1-10)^2+(2-10)^2+(3-10)^2+…+(20-10)^2=570

.

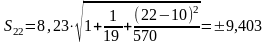Получим интервальные прогнозы:

y21 = 100,3044838 ± 9,526;

y22 = 99,40013471 ± 9,403.