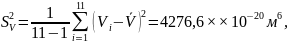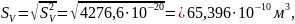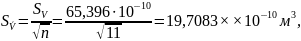Однократные косвенные измерения. Вариант VI

6 Однократные косвенные измерения. Вариант VI

Площадь поперечного сечения рабочего цилиндра S определена по формуле

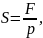
где F – сила, развиваемая поршнем, Н;

p – давление в цилиндре, МПа

Измерение силы проведено динамометром сжатия типа ДОСМ -3 – 2У, а давление измерено цифровым манометром типа ДМ5002А – 10. Значения измеренных величин приведены в таблице А6.

Априорные данные об исследуемом объекте:

Верхний предел измерения силы....................................................................2 кН

Нижний предел измерения силы...................................................................0,2 кН

Предел относительной погрешности динамометра......................................0,5 %

Диапазон измерения манометра...................................................от 0 до 10 кгс/см²

Количество разрядов индикатора манометра........................................................4

Предел допустимой основной относительной погрешности манометра..........................................................................................................................1 %

Измерения проводились в сухом отапливаемом помещении при температуре 22 °С.

Известные систематические погрешности исключены.

Пренебрегая случайной составляющей погрешностью и пользуясь рекомендацией [1] представьте результат однократного косвенного измерения в форме для симметричной доверительной погрешности при Р = 0,95.

Таблица А6 – Исходные данные по варианту VI

Вариант задания	Сила F, кН	Давление p, кгс/см2
VI - 1	1,73	9,01
VI - 2	1,26	7,43
VI - 3	1,18	8,72
VI - 4	1,03	8,34

13

Однократные косвенные измерения. Вариант VII

7 Однократные косвенные измерения. Вариант VII

Электрическое сопротивление цепи R определено по формуле

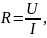
где U – постоянное напряжение (падение напряжения на электрическом сопротивлении цепи);

I – постоянный ток, протекающий в электрической цепи.

Электрическое напряжение измерялось лабораторным вольтамперметром типа М2051 по шкале 1,5 В, а ток – вольтамперметром типа М2044 по шкале 15 мА.

Значения измеренных величин приведены в таблице А7.

Априорные данные об исследуемом объекте:

Верхний предел измерения тока..........................................................................15 мА

Верхний предел измерения напряжения.............................................................1,5 В

Класс точности вольтамперметра М2051............................................................0,5

Класс точности вольтамперметра М2044............................................................0,2

Измерения проводились в нормальных условиях.

Электрическая цепь состоит из постоянных стабильных резисторов.

Известные систематические погрешности исключены.

Пренебрегая случайной составляющей погрешностью и пользуясь рекомендацией [1] представьте результат однократного косвенного измерения в форме для симметричной доверительной погрешности при Р = 0,95.

Таблица А7 – Исходные данные по варианту VII

Вариант задания	Напряжение, В	Ток, мА
VII - 1	1,305	10,88
VII - 2	1,195	10,86
VII - 3	1,110	11,10
VII - 4	1,015	11,15
VII - 5	0,895	10,91
VII - 6	0,820	10,93

14

ПРИЛОЖЕНИЕ Б

(справочное)

Пример многократного косвенного измерения

Определение плотности твердого тела вычисляют по формуле

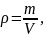
Для определения плотности твердого тела получены результаты измерений аргументов, указанные в таблице Б1.

Погрешности результатов измерений взаимонезависимые (некоррелированные).

Результаты измерений исправлены на действие систематических погрешностей.

При проверке по критерию β (Романовского) грубых погрешностей (промахов) не обнаружено.

Априори известно, что распределение случайных погрешностей аргументов (массы и объема тела) согласуются с нормальным законом распределения.

Зависимость измеряемой величины от аргумента нелинейная, поэтому для нахождения результата измерения и оценки его погрешностей следует воспользоваться методом линеаризации.

Предварительно необходимо проверить, можно ли пренебречь остаточным членом разложения в ряд Тейлора R

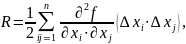
где в качестве ∆х_i и ∆х_j берут наибольшие отклонения из ряда результатов измерений относительно среднего арифметического значения .

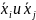Остаточным членом пренебрегают, если

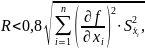
где 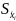- среднее квадратическое отклонение средних значений случайных погрешностей результатов измерения x_i аргумента.

Определим первые и вторые производные в точках

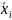
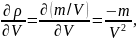
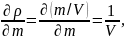
15

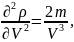
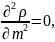
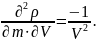
Таблица Б1 – Исходные данные для решения примера

№ п.п.	Масса тела mi∙10-3	кг	кг2	Объем тела Vi∙10-6 м3	м3	м6
1	180,009	9	81	80,0009	9	81
2	180,013	13	169	80,0025	25	625
3	180,015	15	225	80,0064	64	4096
4	180,018	18	324	80,0081	81	6561
5	180,020	20	400	80,0100	100	10 000
6	180,000	0	0	80,0000	0	0
7	179,991	- 9	81	79,9991	- 9	81
8	179,987	- 13	169	79,9975	- 25	625
9	179,985	- 15	225	79,9936	- 64	4096
10	179,982	- 18	324	79,9919	- 81	6561
11	179,980	- 20	400	79,9900	- 100	10 000

,

,

16

Вычислим остаточный член разложения R

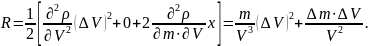
Числовое значение R равно

=

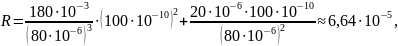
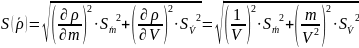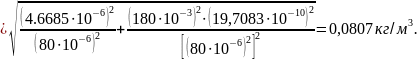
Так как

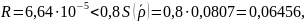
то остаточным членом разложения R можно пренебречь и метод линеаризации допустим.

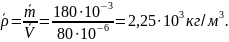
где - среднее квадратическое отклонение средних значений случайных погрешностей результатов измерения x_i аргумента.

Среднее квадратическое отклонение результата измерений

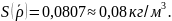
Запись результата измерения можно представить в виде

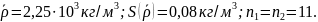
Доверительные границы случайной погрешности результата косвенных измерений при условии, что распределение погрешностей результатов измерений аргументов не противоречит нормальному распределению и (по условию задачи) определяем по формуле

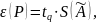
Где t_q – коэффициент Стьюдента, соответствующий доверительной вероятности и числу степеней свободы f_эф.

Задаемся q = 0,05, тогда Р = 1 – 0,05 = 0,95.

17

Вычисляем f_эф по формуле

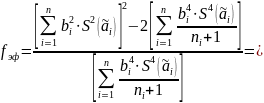
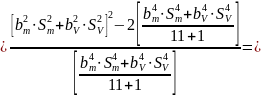
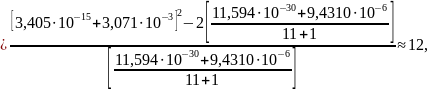
где

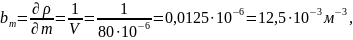
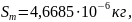
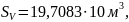
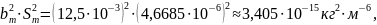
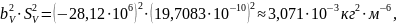
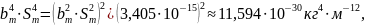
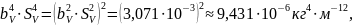
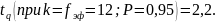
Доверительные границы случайной погрешности

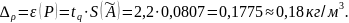
Результат измерения представим в виде

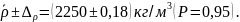
Контрольную работу №3 составил:

Старший преподаватель Крюков В.М. ___________ «____________» 2014г.

Подпись Дата

18
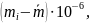
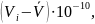
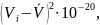
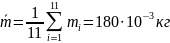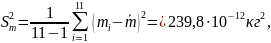
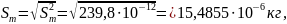
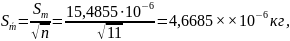
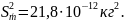
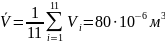