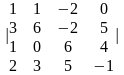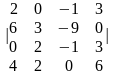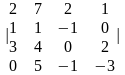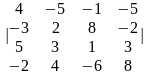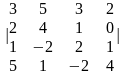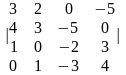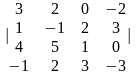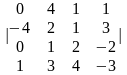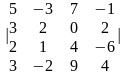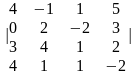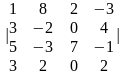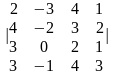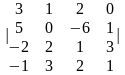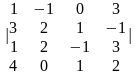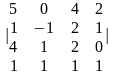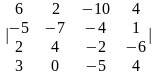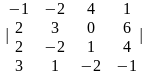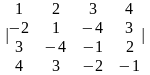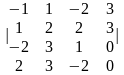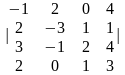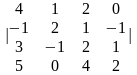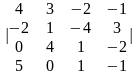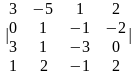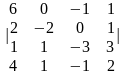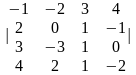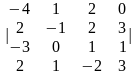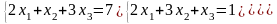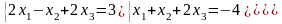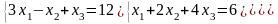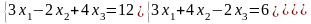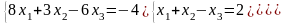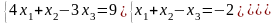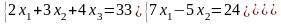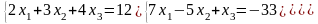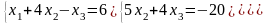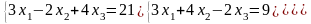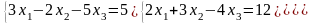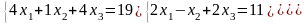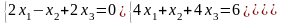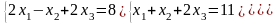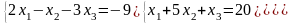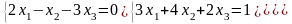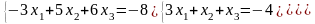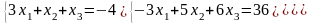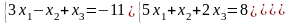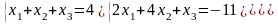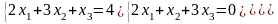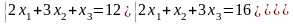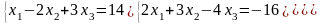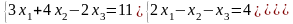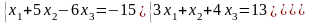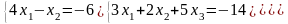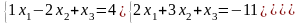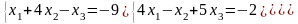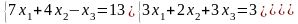МАТЕМАТИКА
ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ №1, №2.
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
Задание 1. Вычислить определитель.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29. |
30. |
|
|
Задание 2. Выполнить действия.
1.
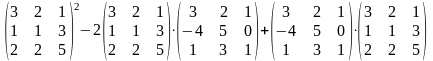
2.
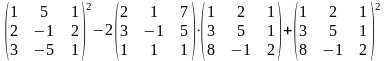
3.
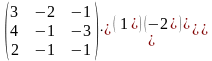
4.
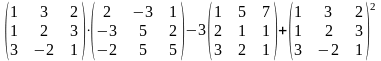
5.
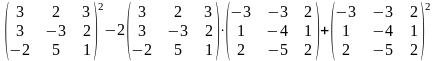
6.
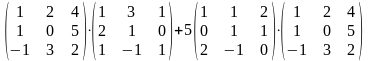
7.
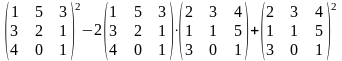
8.
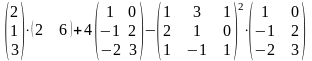
9.
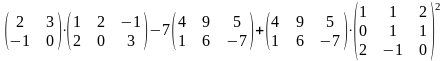
10.
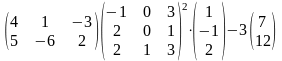
11.
12.
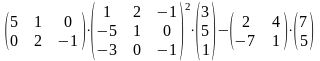
13.
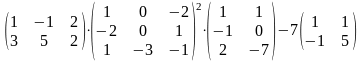
14.
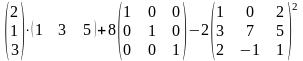
15.
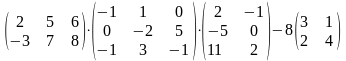
16.
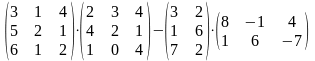
17.
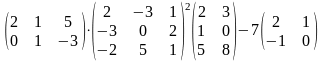
18.
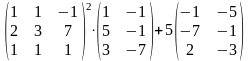
19.
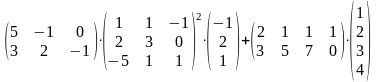
20.
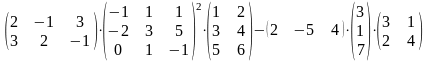
21.
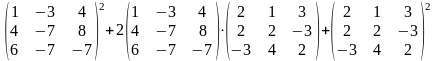
22.
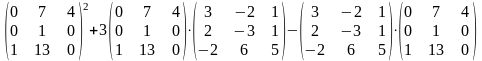
23.
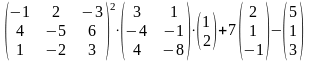
24.
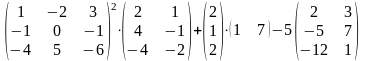
25.
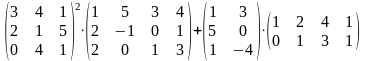
26.
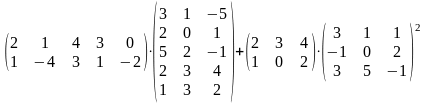
27.
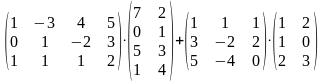
28.
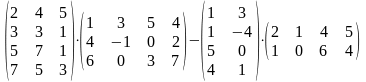
29.
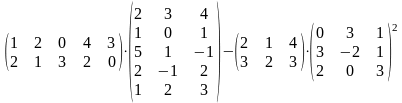
30.
Задание 3. Решить систему линейных уравнений:
а) по формулам Крамера;
б) с помощью обратной матрицы;
в) методом Гаусса или Жордана-Гаусса.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
|
|
Элементы векторной алгебры. Задание 4. Доказать, что векторы образуют базис, и найти координаты вектора в этом базисе.
1.
2.
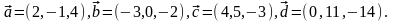
3.
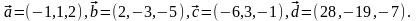
4.
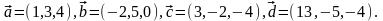
5.
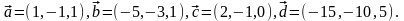
6.
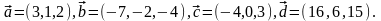
7.
8.
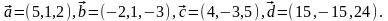
9.
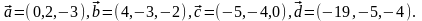
10.
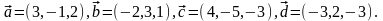
11.
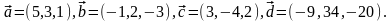
12.
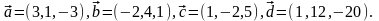
13.
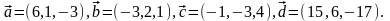
14.
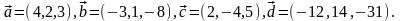
15.
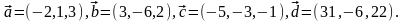
16.
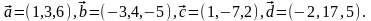
17.
18.
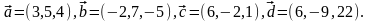
19.
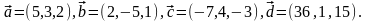
20.
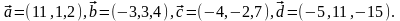
21.
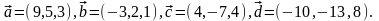
22.
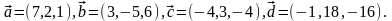
23.
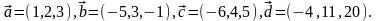
24.
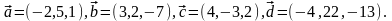
25.
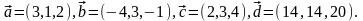
26.
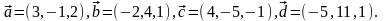
27.
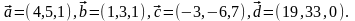
28.
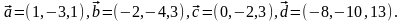
29.
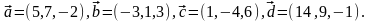
30.
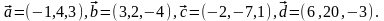
Задание 5. Даны векторы
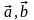и
.
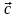Необходимо: а) вычислить смешанное
произведения трех векторов; б) найти
модуль векторного произведения; в)
вычислить скалярное произведение двух
векторов; г) проверить, будут ли коллинеарны
или ортогональны два вектора; д) проверить,
будут ли компланарны три вектора.
1.
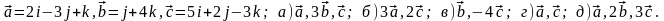
2.
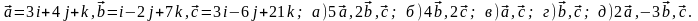
3.
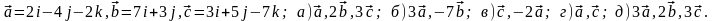
4.
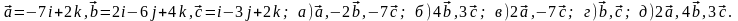
5.
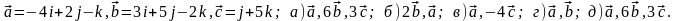
6.
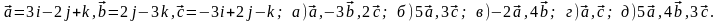
7.
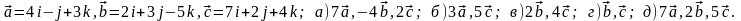
8.
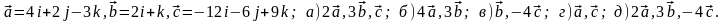
9.
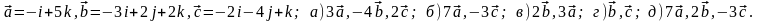
10.
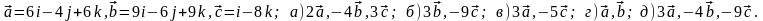
11
12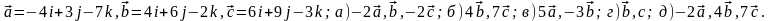
13.
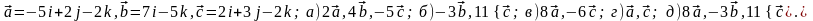
14.
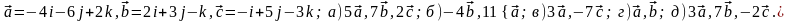
15.
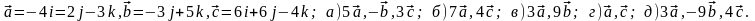
16.
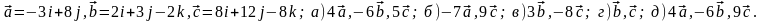
17.
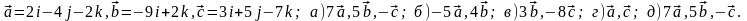
18.
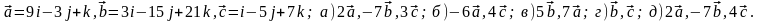
19.
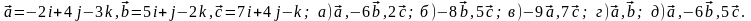
20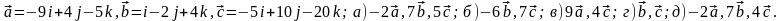
21.
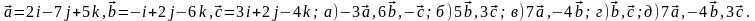
22.
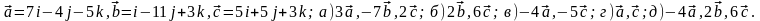
23.
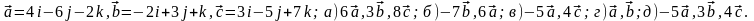
24.
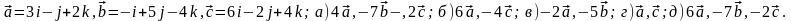
25.
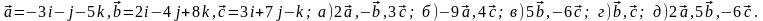
26.
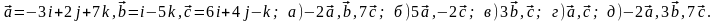
27.
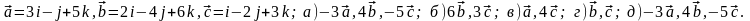
28.
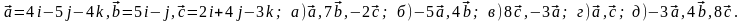
29.
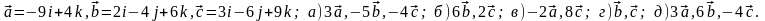
30.
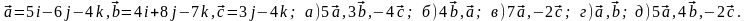
Элементы аналитической геометрии.
Задание 6. Тетраэдр SABC задан координатами вершин в таблице.
Требуется найти:
длины всех его ребер основания;
площади грани основания;
объем тетраэдра;
длину высоты тетраэдра, проведенной из точки S на основание;
уравнения плоскости, содержащей основание тетраэдра;
уравнения прямых, содержащих боковые ребра тетраэдра.
Номер варианта |
S |
A |
B |
C |
1 |
(1,-1,6) |
(2,5,-2) |
(-3,3,3) |
(4,3,-2) |
2 |
(3,6,1) |
(6,1,4) |
(3,-6,10) |
(4,1,5) |
3 |
(1,1,3) |
(6,1,4) |
(6,4,1) |
(7,5,4) |
4 |
(4,4,5) |
(10,2,3) |
(-3,5,4) |
(7,5,4) |
5 |
(-1,2,5) |
(-4,6,4) |
(2,1,5) |
(0,5,6) |
6 |
(2,-1,9) |
(1,1,5) |
(7,3,1) |
(6,-2,2) |
7 |
(1,-2,2) |
(-1,-3,4) |
(5,5,-1) |
(-1,-2,2) |
8 |
(1,1,3) |
(7,1,1) |
(2,2,2) |
(2,6,-2) |
9 |
(3,1,2) |
(5,0,1) |
(0,3,6) |
(2,-4,5) |
10 |
(2,-3,5) |
(0,2,1) |
(-2,-2,3) |
(4,1,-1) |
11 |
(1,1,1) |
(2,0,2) |
(2,2,2) |
(3,7,10) |
12 |
(-1,10,0) |
(0,5,2) |
(6,12,2) |
(3,2,4) |
13 |
(0,1,1) |
(4,3,-3) |
(2,-1,1) |
(3,4,-3) |
14 |
(2,-1,1) |
(5,5,4) |
(6,3,7) |
(0,0,0) |
15 |
(2,3,1) |
(4,1,-2) |
(2,-1,3) |
(0,1,0) |
16 |
(2,1,-1) |
(3,0,1) |
(3,1,1) |
(4,3,1) |
17 |
(1,0,0) |
(-1,1,2) |
(2,5,0) |
(-5,-4,8) |
18 |
(2,-1,0) |
(3,1,1) |
(3,1,0) |
(0,8,0) |
19 |
(3,0,1) |
(1,2,2) |
(3,1,2) |
(-1,10,2) |
20 |
(1,-1,1) |
(2,1,1) |
(2,2,2) |
(7,0,1) |
21 |
(-1,2,1) |
(0,1,2) |
(3,0,1) |
(-1,-5,1) |
22 |
(3,1,1) |
(2,1,1) |
(2,1,-1) |
(1,0,3) |
23 |
(2,1,0) |
(3,0,1) |
(3,2,1) |
(1,3,2) |
24 |
(5,0,0) |
(6,1,1) |
(-1,-1,0) |
(2,2,-1) |
25 |
(1,-1,1) |
(2,1,-1) |
(1,3,-4) |
(3,2,1) |
26 |
(0,1,1) |
(3,2,1) |
(3,-2,-1) |
(4,1,1) |
27 |
(3,0,-3) |
(1,2,1) |
(3,-1,-4) |
(2,1,1) |
28 |
(1,2,3) |
(3,2,1) |
(4,0,1) |
(2,0,2) |
29 |
(7,0,0) |
(5,-1,1) |
(4,2,3) |
(2,1,1) |
30 |
(7,0,3) |
(3,0,-1) |
(3,0,5) |
(4,3,-2) |