Основные законы логики высказываний

Следующие законы являются логическими следствиями введенных булевых операций и доказываются, как теоремы, с применением таблиц истинности. Перечислим эти законы.

1. Коммутативность конъюнкции: .

2. Коммутативность дизъюнкции: .

3. Ассоциативность конъюнкции: .

4. Ассоциативность дизъюнкции: .

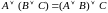5. Дистрибутивность конъюнкции относительно дизъюнкции: .

6. Дистрибутивность дизъюнкции относительно конъюнкции: .

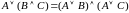7. Закон де Моргана относительно конъюнкции: .

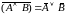8. Закон де Моргана относительно дизъюнкции: .

9. Закон поглощения для дизъюнкции: .

10. Закон поглощения для конъюнкции: .

11. Закон идемпотентности для конъюнкции: .

12. Закон идемпотентности для дизъюнкции: .

13. Закон противоречия: .

14. Закон исключения третьего: .

15. Закон двойного отрицания: .

16. , .

17. , .

Равенства в приведенных законах означает совпадение значений левой и правой частей равенства при любых значениях входящих в выражение высказываний.

Доказательство каждого закона представляет собой составление таблицы истинности, перебор всевозможных значений входящих в закон высказываний и сравнение значений высказываний левой и правой частей равенства. Приведем примеры доказательств законов 5 и 7.

Для доказательства закона 5, зададим всевозможные наборы значений для множеств и (первые три столбца).

И	И	И	И	И	И	И	И
Л	И	И	И	Л	Л	Л	Л
Л	Л	И	И	Л	Л	Л	Л
Л	Л	Л	Л	Л	Л	Л	Л
И	Л	Л	Л	Л	Л	Л	Л
И	И	Л	И	И	И	Л	И
Л	И	Л	И	Л	Л	Л	Л
И	Л	И	И	И	Л	И	И

Заполним 4-й, 6-й и 7-й столбцы в соответствии с аксиоматически заданными таблицами значений для соответствующих операций. После этого заполним 5-й и 8-й столбцы. Мы видим, что значения на соответствующих строках совпадают. Закон доказан.

Аналогичным способом доказывается 7-й закон:

И	И	И	Л	Л	Л	Л
Л	И	Л	И	И	Л	И
И	Л	Л	И	Л	И	И
Л	Л	Л	И	И	И	И

Студенты должны самостоятельно доказать остальные законы.

Полученные законы мы сможем применять для упрощения сложных высказываний.