
- •Варианты контрольных работ подготовили:
- •Предисловие
- •Введение
- •Основные правила приближенных вычислений
- •Содержание дисциплины и методические рекомендации по ее изучению
- •Часть 1. Линейная алгебра
- •Раздел I. Элементы матричного анализа
- •Тема 1. Матрицы и определители
- •Тема 3. Векторные пространства
- •Раздел II. Элементы аналитической геометрии
- •Тема 4. Элементы аналитической геометрии
- •Часть 2. Математический анализ
- •Раздел iIl. Введение в анализ
- •Тема 5. Функции
- •Тема 6. Пределы и непрерывность
- •Раздел IV. Дифференциальное исчисление
- •Тема 7. Производная
- •Тема 8. Приложения производной
- •Тема 9. Дифференциал функции
- •Тема 10. Функции нескольких переменных
- •Раздел V. Интегральное исчисление и дифференциальные уравнения
- •Тема 11. Неопределенный интеграл
- •Тема 12. Определенный интеграл
- •Вопросы для самопроверки
- •Часть I. Линейная алгебра
- •Часть 2. Математический анализ
- •Задачи для самоподготовки
- •Методические указания по выполнению контрольных работ
- •Варианты контрольных работ вариант 1
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 2 (для студентов, номера личных дел которых оканчиваются цифрой 2) Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 4
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 5
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 6
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 7
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 8
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Примеры выполнения заданий контрольных работ
- •Решения задач типовых вариантов
- •Литература Основная1
- •Дополнительная
- •Электронные ресурсы
- •Содержание
- •Математика.
Раздел II. Элементы аналитической геометрии
Тема 4. Элементы аналитической геометрии
Уравнение линии на плоскости. Уравнение прямой с угловым коэффициентом и начальной ординатой. Общее уравнение прямой и его исследование. Построение прямой по ее уравнению. Уравнение прямой, проходящей: а) через данную точку в данном направлении; б) через две данные точки. Координаты точки пересечения двух прямых. Условие параллельности и перпендикулярности прямыхУравнение плоскости в пространстве и его частные случаи. Условие параллельности и перпендикулярности плоскостей.. Угол между двумя плоскостями. ([1 или 6, § 4.1 – 4.3, 4.6, 4.7]; [2 или 7, § 4.1 – 4.3], или [3, § 4.2 – 4.6, 4.8 – 4.10, 4.12], или [4, § 4.2 – 4.6, 4.8 , 4.12, 4.13, 4.15].
По используемым методам аналитическая геометрия существенно отличается от элементарной геометрии. Применение основного метода аналитической геометрии – метода координат позволяет значительно продвинуть вперед изучение геометрических образов, исследовать линии и поверхности, важные для практических приложений.
Важнейшим понятием аналитической геометрии является уравнение линии на плоскости, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Из этого определения следует два важных для практики положения.
1. Если задано уравнение линии, то можно установить, принадлежит ли ей какая-либо точка плоскости. Для этого достаточно подставить координаты точки в уравнение линии вместо переменных x и y. Если окажется, что они удовлетворяют уравнению, то точка принадлежит линии, в противном случае – не принадлежит.
2. Координаты точки пересечения двух линий, заданных своими уравнениями, удовлетворяют обоим уравнениям. Поэтому для нахождения координат точки пересечения двух линий нужно решить систему, составленную из их уравнений.
Следует отметить, что решение задач в аналитической геометрии проводится алгебраическим путем и никакие ссылки не чертеж не могут служить обоснованием решения задачи. Чертежи и геометрические построения служат вспомогательным средством, облегчающим решение задачи, делающим его наглядным, помогающим наметить план решения задачи. Поэтому рекомендуется сопровождать решение чертежами.
Из всех линий прямая линия имеет особое значение. Она (и ее обобщение в n-мерном пространстве) является графиком линейной функции, используемой в наиболее часто встречающихся на практике линейных экономико-математических моделях, которые будут изучаться в курсе «Методы оптимальных решений».
Студент должен знать уравнения прямой с угловым коэффициентом и начальной ординатой и его частные случаи; уравнение прямой, проходящей через данную точку в заданном направлении и через две данные точки, общее уравнение прямой [1, или 6, или 3, § 4.1]. Обратите внимание на условия параллельности и перпендикулярности прямых; на нахождение уравнения прямых; параллельной и перпендикулярной данной прямой [1, или 6, или 3, пример 4.5].
Обобщением уравнения прямой
на плоскости является уравнение плоскости
в пространстве
 (обобщением которого, в свою очередь,
является уравнение гиперплоскости в
n-мерном
пространстве, рассматриваемое в
прикладных математических курсах). Надо
знать смысл его коэффициентов А,
В,
С
(как координат нормального вектора
плоскости) и частные случаи уравнения
плоскости. Например, уравнение плоскости:
проходящей через начало координат,
(обобщением которого, в свою очередь,
является уравнение гиперплоскости в
n-мерном
пространстве, рассматриваемое в
прикладных математических курсах). Надо
знать смысл его коэффициентов А,
В,
С
(как координат нормального вектора
плоскости) и частные случаи уравнения
плоскости. Например, уравнение плоскости:
проходящей через начало координат,
 (
( );
параллельной оси Оу,
);
параллельной оси Оу,
 (
(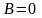 );
проходящей через ось Оу,
);
проходящей через ось Оу,
 (
( );
параллельной плоскости Oxz,
);
параллельной плоскости Oxz,
 (
( );
совпадающей с плоскостью Oxz,
);
совпадающей с плоскостью Oxz,
 ,
т.е.
,
т.е.
 ,
(
,
(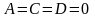 )
и т.д.
)
и т.д.
Обращаем внимание на то, что направление плоскости определяется нормальным вектором, поэтому углы между двумя плоскостями сводятся к определению углов между этими векторами. Отсюда вытекают условия параллельности и перпендикулярности двух плоскостей.
Основные типы задач на плоскость в пространстве представлены задачами с решениями [2 или 7, примеры 4.87, 4.88] или [3, примеры 4.108 – 4.109]. Решение отдельных задач предполагает знание скалярного произведения двух векторов (но не требует знания векторного и смешанного произведения векторов, не входящими в программу).
