Вариант 8
(для студентов, номера личных дел которых оканчиваются цифрой 8)
Контрольная работа № 1
1. Даны матрицы
и
Определить, имеет ли матрица обратную.
2. По формулам Крамера решить систему:
3. Решить систему линейных уравнений:
Найти какое-нибудь базисное решение.
4. Даны четыре вектора
=(1;1;1); =(0;2;3); =(0;1;5); =(2; –1;1)
в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе.
5. Вычислить
площадь квадрата, если две его стороны
лежат на прямых
,
.
6
Написать уравнение плоскости, проходящей
через точку
параллельно векторам
и
.
Контрольная работа № 2
1. Найти предел:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
.
в точках пересечения ее с параболой
.
Сделать чертеж.
и построить схематично ее график.
,
,
и расположенной в первой четверти
координатной плоскости. Сделать
чертеж.
.
Используя метод наименьших квадратов,
аппроксимировать эти данные линейной
зависимостью
(найти параметры а
и b).
Выяснить, какая из двух линий лучше
(в смысле метода наименьших квадратов)
выравнивает экспериментальные
данные. Сделать чертеж.
и
обратную.
является центром квадрата, одна из
сторон которого лежит на прямой
.
Составить уравнение прямой, на
которой лежит параллельная ей сторона
этого квадрата.
и
.
.
в точке с ординатой, равной 4. Сделать
чертеж.
и построить схематично ее график..
,
,
и расположенной в первой четверти
координатной
Используя метод наименьших
квадратов,
и
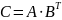обратную.
и
соответственно, а одна из вершин,
лежащих
и
.
.
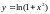в точке с абсциссой, равной 1.
Сделать чертеж.
и схематично построить ее
график.
,
,
.
Сделать чертеж.
.
Используя метод наименьших
квадратов,