2. Лабораторная работа №2 Численные методы решения скалярных уравнений

Цель работы: сформировать у студентов представление о применении уравнений в различных областях деятельности, привить знания об основных этапах решения уравнения, выработать навыки использования различных методов для уточнения корня уравнения и выбора того или иного программного средства для проверки правильности найденного результата.

2.1. Метод хорд

Пример 2.1.

Решить уравнение е^х ∙ (2 – х) – 0,5 = 0 методом хорд с точностью ɛ = 0,001.

Решение.

1. Отделяем корни. Этот этап решения осуществляется с помощью аналитического или графического метода. После того как корень, подлежащий уточнению, отделен, за начальное приближение может быть выбрана любая точка [a,b] (начало отрезка, его середина и т.д.).

Воспользуемся графическим методом. Построим график функций и найдем точки пересечения его с осью Ох (рис.2.1.).

f(x) = (2 – x) (e^x) – 0,5

x = -4, -3,99..5

Рис.2.1. Отделение корней графически

Получили два интервала: [-3; -2], [1,5; 2,5]. Интервал, в котором мы будем уточнять корень – [1,5; 2,5].

2. Уточняем корни. Находим первую производную функции

f(x) = e^x ∙ (2 – x) – 0,5:

3. Определяем знаки f(x) на отрезке [1,5; 2,5]:

f(1,5) = 1,741>0, f(2,5) = -6,591<0

Значит, на данном отрезке действительно существует корень нашего уравнения.

4. Строим последовательность значений с использованием рекуррентной формулы метода хорд и проанализируем результаты вычисленных значений последовательности х_п (рис.1.2). Для этого рассмотрим значения функции dz(x_n) – эта величина является критерием достижения заданной точности ɛ = 0,001. Начиная с п = 8, значение х_п удовлетворяют критерию достижения заданной точности (ɛ > 8,801∙ 10^-4), значит х₈ = 1,927 является решением нашего уравнения.

п = 0...10

х₀=а

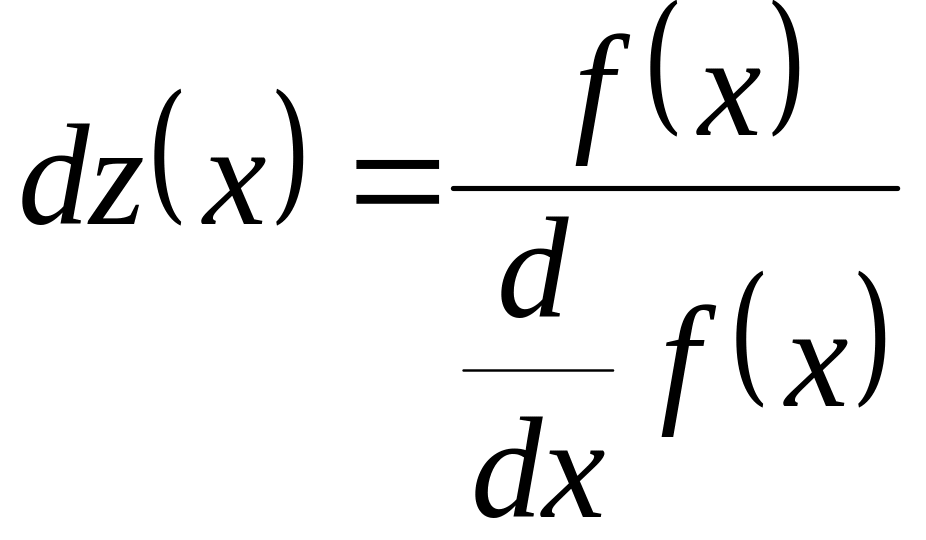
Рис. 2.2. Проверка критерия достижения

заданной точности

5. Создаем функцию, реализующую вычисления корня уравнения

е^х∙ (2 – х) – 0,5 = 0 на отрезке [1,5; 2,5] с точностью ɛ = 0,001 методом хорд (рис. 2.3). Решением будет являться число 1,927, получившееся на третьем шаге решении

Рис.2.3. Функция, возвращающая значения корня уравнения методом хорд.

Аргументы функции: а, b – концы отрезка; – погрешность вычислений,

f 1pr(x) – функция первой производной

6. Проверяем решение уравнения встроенными функциями Матhcad

1) х = 2

хl = root(f(x),x) xl = 1,927

2) Given

(2 – x)∙(e^X) – 0,5 = 0

x2 = Find(x) x2 = 1,927

2.2. Метод касательных

Пример 2.2.

Вычислить методом касательных корень уравнения е^х∙(2 – х) –0,5=0 на отрезке[1,5; 2,5] с точностью ɛ = 0,001.

Решение.

1. Отделяем корни уравнения (см. разд. 2.1).

2. Определяем неподвижную точку.

Для этого определим знаки функции и второй производной на отделенном интервале [1,5; 2,5]. Для этого составим функцию, проверяющую условие неподвижности точки

а = 1,5 b = 2,5

f(x) = (2 – x)(e^x) – 0,5

nt = 2.5

Тогда подвижной точкой будет точка а = 1,5.

3. Вычисляем значение итерационной последовательности с использованием рекуррентной формулы метода касательных (рис. 2.4).

х ₀ = а

Рис. 2.4. Построение итерационной последовательности

по методу касательных

Анализируя полученные значения для достижения критерия заданной точности, можно сказать, что решением уравнения будет значение

х₄ = 1,927 при п = 4, т.к. 2,367∙10^-5 ˂ 0,001.

4. Создаем функцию, реализующую метод касательных (аналогично методу хорд).

5. Проверяем полученные результаты.

Отметим, что в пакете Mathcad имеется еще несколько функций, позволяющих решать уравнения, например, функция solve, вызываемая с панели Symbolic (рис. 2.5.)

Рис. 2.5. Панель Symbolic

Пример использования команды solve представлен на рис. 2.6.

Рис.2.6. Решение уравнения с помощью команды solve