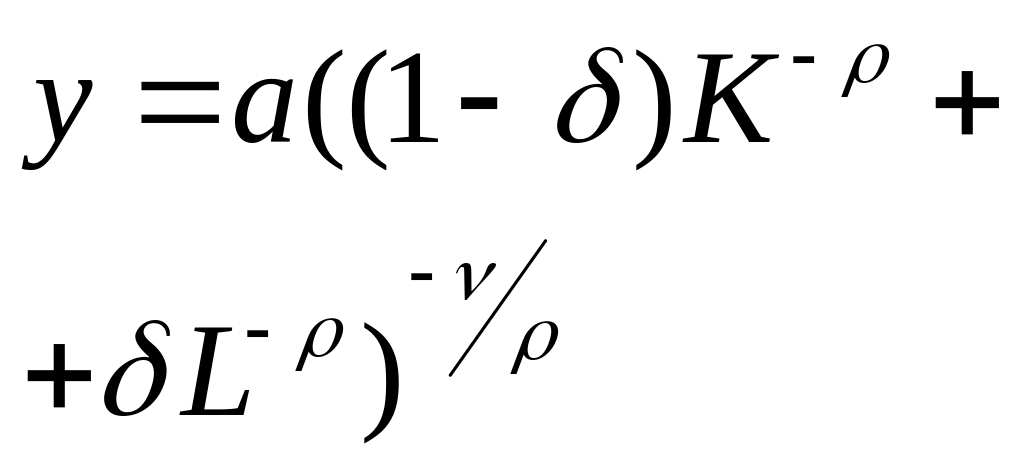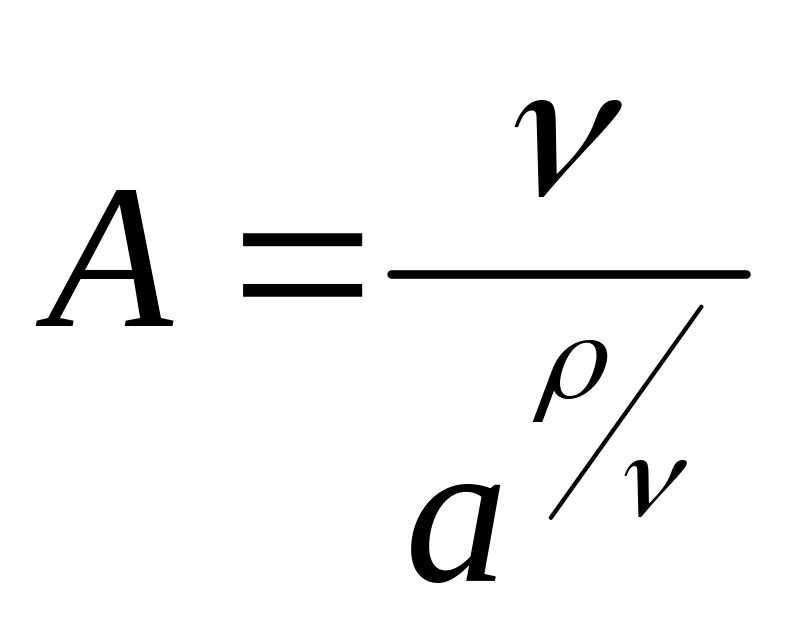Еластичність випуску за ресурсами і еластичність заміни ресурсів

Еластичність випуску за ресурсами.

Визначення. Коефіцієнтом еластичності випуску за витратами j-го ресурсу називається відносний приріст випуску (в %), викликаний відносним приростом ресурсу на 1%.

E_j .

Еластичність заміни ресурсів Е_ij.

Визначення. Коефіцієнтом еластичності заміни j-го ресурсу i-м Е_ji називається відносний приріст відношення i-го і j-го ресурсів, викликаний відносним приростом граничної норми заміни j-го ресурсу i-м на 1% при незмінному рівні випуску.

.

Інакше кажучи, Е_ji показує на скільки відсотків повинне змінитися відношення ресурсів при русі уздовж ізокванти, щоб при цьому гранична норма заміни (тангенс кута нахилу ізокванти) змінилася на один відсоток.

Для макроекономічної ВФ

Коефіцієнт еластичності заміни пов'язаний з мірою кривизни ізокванти, причому більш опуклі до початку координат ізокванти відповідають меншим коефіцієнтам еластичності заміни.

Еластичність заміни ресурсів характеризує можливість їх взаємозамінності.

При Е_KL= при будь-яких значеннях L і при будь-якому об'ємі випуску Y₀ можна підібрати таке значення К, яке компенсують будь-які зміни L, причому _KL=const. ( лінійна ВФ).

При зменшенні Е_KL для будь-якого Y₀ і будь-якого L теж можна визначити відповідне К, але норма заміни буде все більше і більше зростати. При подальшому зменшенні Е_KL<1 взаємозамінність ресурсів обмежена, тобто достатньо велику зміну витрат праці вже не можна компенсувати ніякими змінами витрат (функція Кобба-Дугласа, функція CES)_.

Коли Е_KL=0 взаємозамінність ресурсів неможлива. Ресурси стають взаємодоповнювальними (функція Леонтьєва).

Типові виробничі функції

Розглянемо найбільш поширені двофакторні функції, які використовуються в макроекономічному аналізі. Усі ці функції можуть бути отримані за допомогою граничного переходу із функції з постійною еластичністю заміщення (constant elasticity of substitution, CES).

Функція з фіксованими пропорціями чинників (функція Леонтьєва, функція „витрати-випуск”).

y=min(aK, bL),

де a, b – параметри.

Функція Леонтьєва призначена в основному для моделювання строго детермінованих технологій, які не допускають відхилення від технологічних норм і нормативів щодо використання ресурсів на одиницю продукції. Як правило, вона використовується для формалізованого опису дрібномасштабних або цілком автоматизованих об'єктів.

Дана функція є однорідною, з еластичністю заміни чинників, що дорівнює нулю.

Вона може бути отримана з функції з постійною еластичністю виду

шляхом граничного переходу: .

Функція Кобба-Дугласа: y=AK^L^.

Дана функція має наступні властивості:

еластичності випуску за чинниками є постійними і дорівнюють показникам степеня за кожним чинником (див. табл. 4.1);

функція є однорідною відносно K та L;

гранична продуктивність кожного чинника пропорційна його середній продуктивності;

функція може бути отримана з функції з постійною еластичністю шляхом граничного переходу: 0.

Функція Кобба-Дугласа найчастіше використовується при моделюванні середньомасштабних господарських об'єктів та економіки країни.

Лінійна функція.

y=aK+bL.

Ця функція задовольняє таким гіпотезам.

граничні продуктивності чинників є постійними (див. табл. 4.1), а в нулі функція набуває нульового значення;

функція однорідна, й еластичність заміни чинників є нескінченною;

еластичність випуску за чинниками обернено пропорційна їхній середній продуктивності.

Лінійна функція застосовується для моделювання великомасштабних систем (велика галузь, народне господарство в цілому), у яких випуск продукції є результатом одночасного функціонування великої кількості різноманітних технологій. Особливу роль відіграє гіпотеза постійності граничних виробничих чинників чи їх необмеженого заміщення.

Функція постійної еластичності заміщення чинників (фунщія CES):

,

Тут -1;  - cтепень однорідності; A>0; 0<<1.

Функція є однорідною, й еластичність заміщення чинників є постійною.

Функція CES застосовується у разі відсутності точної інформації щодо рівня взаємозаміни виробничих чинників, і разом з тим є підстави вважати, що цей рівень суттєво не зміниться за зміни обсягів залучених ресурсів, тобто коли економічна технологія має властивість певної стійкості щодо певних пропорцій чинників. Функція СES (за наявності засобів оцінки її параметрів) може використовуватись для моделювання систем будь-якого рівня.

В наукових дослідженнях використовуються й інші виробничі функції, наприклад,

функція Аллена : ,

функція Солоу: ,

багаторежимна функція: тощо.

З властивостями цих функцій можна ознайомитись, звернувшись до літе-ратурних джерел, наведених наприкінці розділу. Щодо основних властивостей і характеристик розглянутих функцій, то вони подані далі в таблиці 6.4.

Таблиця 6.4- Типові виробничі функції та їх основні характеристики

Тип ВФ	Вид ізоквант	Гранична продуктивність праці	Гранична фондовіддача	Еластичність за фондами	Еластичність праці	Гранична норма заміщення	Еластичність заміщення
Лінійна y=aK+bL		b	a			b/a	
Кобба-Дугласа y=AKL		AKL-1	AK-1L				1
Леонтьева y=min(aK, bL)						0	0
СES		где	где	где	где		1/(1+)