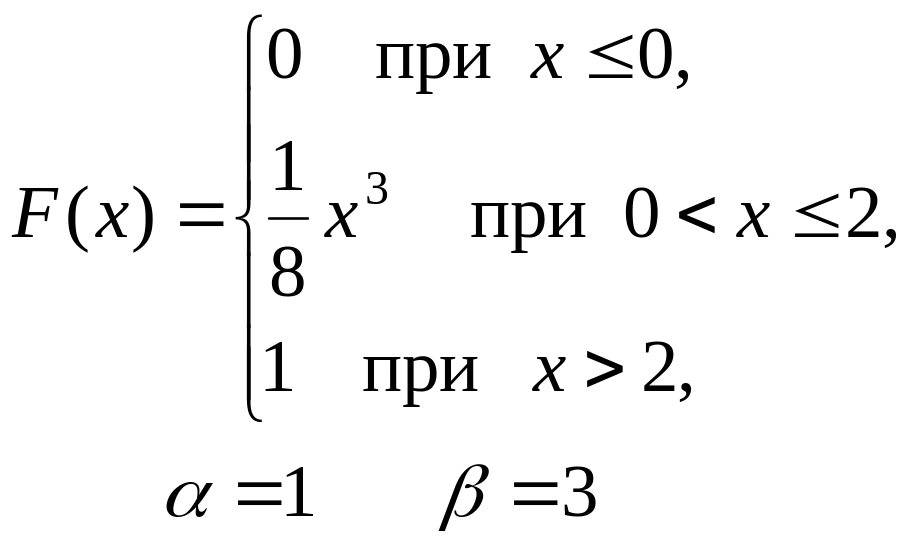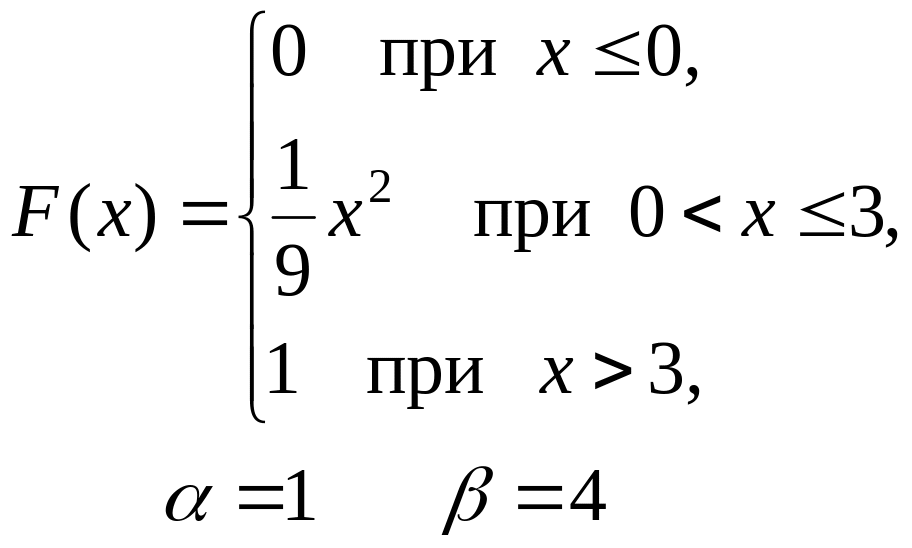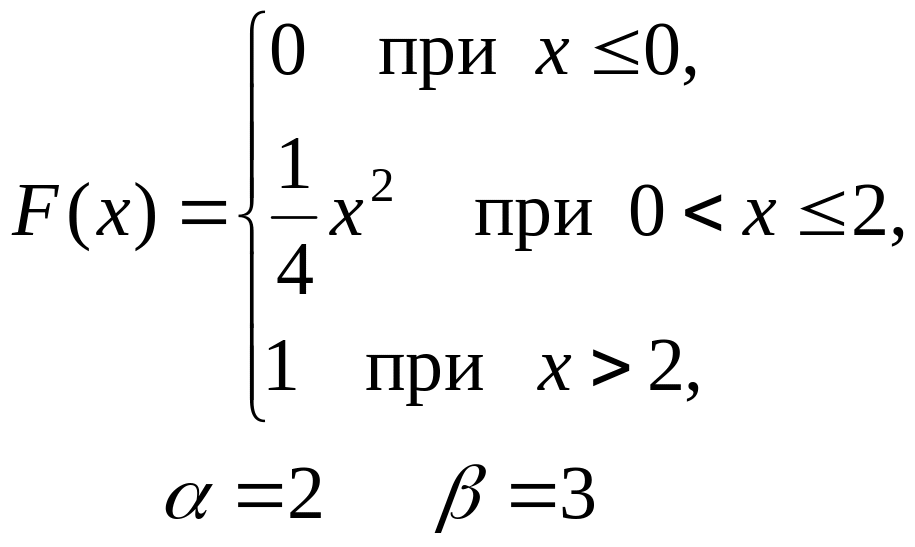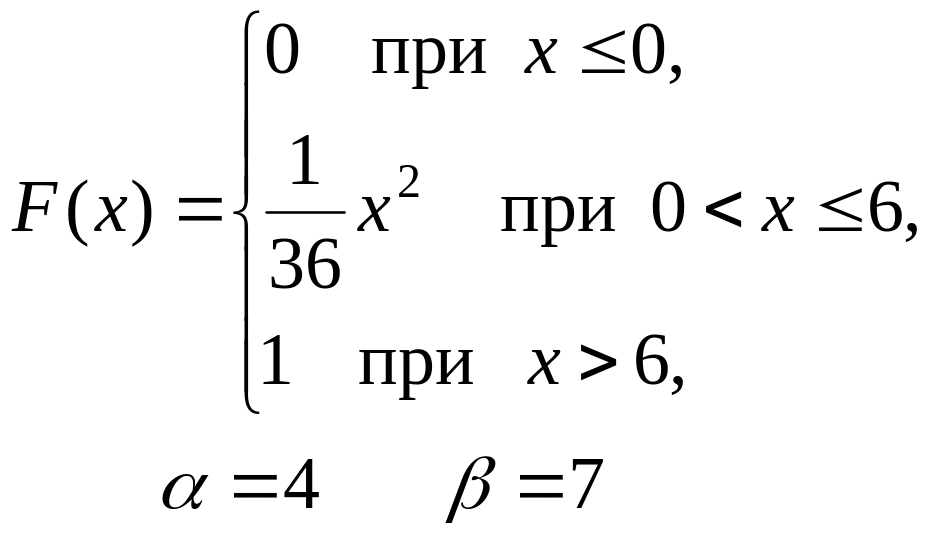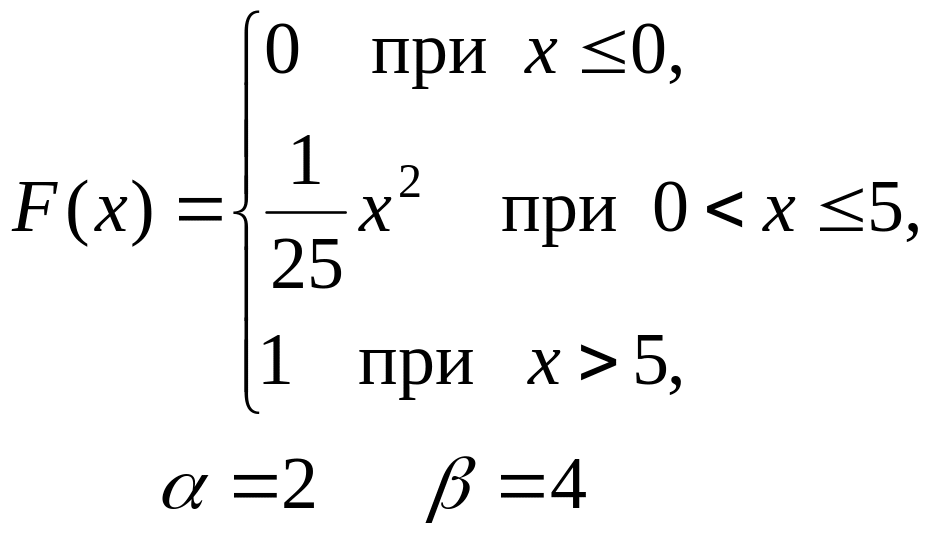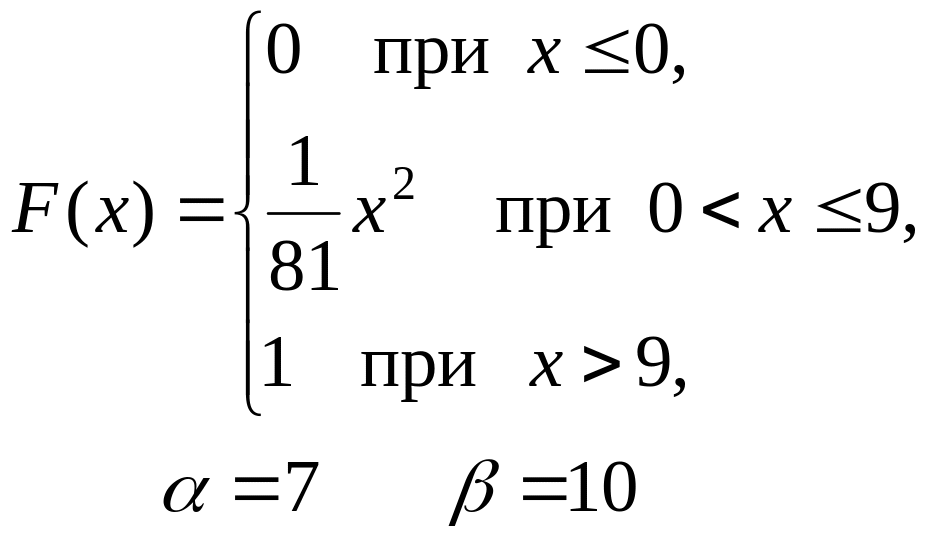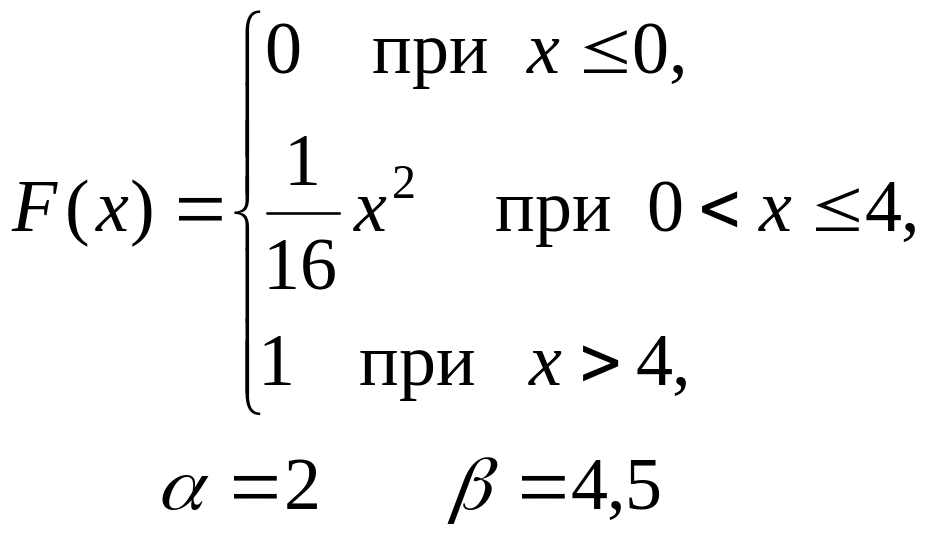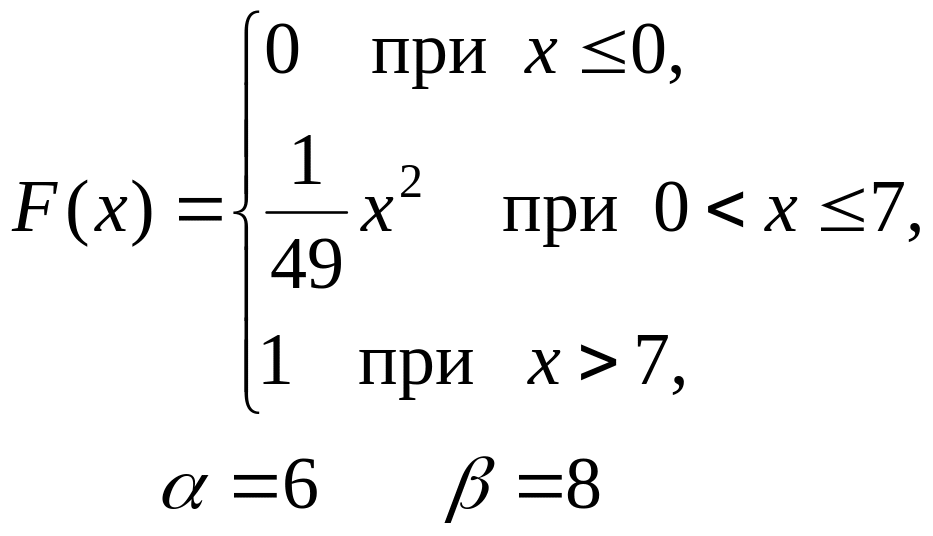Контрольная работа №6 Теория вероятностей

1. В ящике имеются десять белых и пятнадцать черных шаров. Наудачу извлекают пять шаров. Найти вероятность того, что среди них будет ровно два белых шара.

2. В цехе работают шесть мужчин и четыре женщины. Наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.

3. В партии готовой продукции, состоящей из 20 изделий, четыре бракованных. Найти вероятность того, что при случайном выборе четырех изделий число бракованных и не бракованных изделий окажется одинаковым.

4. На складе 25 подарков, причем пятнадцать из них московской фабрики. Найти вероятность того, что среди взятых наудачу четырех подарков окажется три подарка московской фабрики.

5. В мастерскую для ремонта поступило 20 мобильных телефонов. Известно, что семь из них нуждаются в настройке. Мастер берет пять телефонов (любые). Какова вероятность того, что два из них нуждаются в настройке?

6. Вероятность поражения цели первым стрелком равна 0,8, вторым – 0,7. Оба стрелка сделали по одному выстрелу. Какова вероятность того, что цель поражена только один раз?

7. Вероятность того, что студент сдаст первый экзамен, равна 0,8, второй – 0,6, третий – 0,5. Найти вероятность того, что студент сдаст не менее двух экзаменов.

8. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы за время t первого, второго и третьего элементов соответственно равны 0,5; 0,7; 0,9. Найти вероятность того, что за время t безотказно будет работать только один элемент.

9. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,3; 0,6; 0,7. Найти вероятность того, что эта формула содержится не менее чем в двух справочниках.

0. Три работника работают независимо друг от друга. Вероятность допустить ошибку для первого равна 0,1, для второго – 0,2, для третьего – 0,15. Найти вероятность того, что за смену допустят ошибку два работника.

1. Вероятность выигрыша по лотерейному билету равна 0,15. Найти вероятность того, что из восьми купленных билетов выигрышными окажутся: а) три; б) не менее двух.

2. Вероятность работы каждой из семи телефонных линий в данный момент равна 0,8. Найти вероятность того, что в данный момент работают: а) две линии; б) менее трех линий.

3. Всхожесть семян составляет 90%. Чему равна вероятность того, что из семи посеянных семян взойдут: а) четыре; б) более четырех?

4. В магазин вошли десять покупателей. Вероятность совершить покупку для каждого покупателя одна и та же и равна 0,25. Найти вероятность того, что совершат покупку: а) три покупателя; б) не более трех.

5. Вероятность малому предприятию быть банкротом за месяц равна 0,2. Найти вероятность того, что из шести малых предприятий за месяц обанкротятся: а) два; б) более трех.

6. В среднем по 25% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы: а) четыре договора; б) менее двух договоров.

7. Вероятность перевыполнения годового плана для каждого из восьми рабочих равна 0,7. Найти вероятность того, что перевыполнят план: а) трое рабочих; б) более шести.

8. Предполагается, что 15% открывающихся малых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из шести малых предприятий прекратят свою деятельность в течение года: а) два; б) не более трех?

9. Вероятность приема радиосигнала при каждой передаче равна 0,8. Найти вероятность того, что при передаче сигнала пять раз он будет принят: а) два раза; б) не менее четырех раз.

0. В семье пять детей. Найти вероятность того, что среди этих детей: а) три мальчика; б) не более трех мальчиков. Вероятность рождения мальчика и девочки считать одинаковой.

191–200. Дискретная случайная величина Х задана законом распределения.

Найти: а) p; б) M(X); в) D(X); г) M(X+).

№ задания	Закон распределения	№ задания	Закон распределения
191	X 1,4 1,8 2,3 3,2 3,5 p 0,2 p 0,4 0,2 0,1  = 2  = -3	192	X 0,2 0,4 0,7 0,8 1,0 p 0,1 0,15 p 0,2 0,3  = 1  = 2
193	X 0,1 0,2 0,3 0,4 0,5 p 0,2 0,25 0,15 p 0,1  = 4  = -1	194	X 1,2 1,4 1,6 1,8 2,0 p 0,1 0,2 p 0,15 0,25  = -3  = 2
195	X 0,15 0,25 0,35 0,45 0,55 p 0,3 0,2 0,25 p 0,1  = 2  = 4	196	X -1,1 0,1 1,1 2,1 3,1 p 0,1 p 0,2 0,25 0,3  = -3  = 1
197	X 1,3 2,3 3,3 4,3 5,5 p 0,2 0,15 p 0,1 0,3  = 4  = -2	198	X 0,11 0,21 0,31 0,41 0,51 p 0,1 0,15 p 0,3 0,2  = 3  = -3
199	X -2,1 -1,1 0 1,1 2,1 p 0,1 0,15 0,35 p 0,1  = 3  = 2	200	X 3,2 4,2 5,2 6,2 7,2 p 0,2 p 0,16 0,34 0,1  = 5  = -1

201–210. Дана функция распределения F(x) случайной величины X.

Найти: а) плотность распределения вероятностей f(x);

б) математическое ожидание M(X);

в) вероятность попадания случайной величины X в интервал (, ).

Построить графики функций F(x) и f(x).

№ задания	Закон распределения	№ задания	Закон распределения
201		202
203		204
205		206
207		208
209		210