Министерство образования и науки Российской Федерации

Костромской государственный технологический университет

Кафедра высшей математики

Л.А. Ширина

Математика

Учебно-методическое пособие

для студентов заочной формы обучения

по направлению подготовки «Технологии продукции и организации общественного питания»

Кострома

КГТУ

2015

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 3

ОБЩИЕ ТРЕБОВАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ 3

РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ «МАТЕМАТИКА» 4

КОНТРОЛЬНАЯ РАБОТА №1 7

КОНТРОЛЬНАЯ РАБОТА №2 8

КОНТРОЛЬНАЯ РАБОТА №3 11

КОНТРОЛЬНАЯ РАБОТА №4 13

КОНТРОЛЬНАЯ РАБОТА №5 14

КОНТРОЛЬНАЯ РАБОТА №6 16

Список рекомендуемой литературы 20

Приложение 1 21

Приложение 2 21

Приложение 3 22

Приложение 4 23

Введение

Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебникам, решение задач, выполнение контрольных работ. В помощь заочникам кафедра высшей математики университета организует чтение обзорных лекций в начале и в конце каждого семестра и еженедельные консультации в течение семестра. Кроме того, студент может обращаться к преподавателю с вопросами в письменном виде или устно. Указания студенту по текущей работе даются также в процессе рецензирования контрольных работ. Однако студент должен помнить, что только при системной упорной работе помощь кафедры окажется достаточно эффективной. Завершающим этапом изучения отдельных разделов курса математики является сдача экзаменов и зачетов в соответствии с учебным планом.

Общие требования по выполнению контрольных работ

В процессе изучения курса математики студент должен выполнить шесть контрольных работ, главная цель которых – проверить знания и навыки, полученные в процессе самостоятельного освоения изучаемого материала. При выполнении контрольных работ студент должен руководствоваться следующими указаниями.

• Не приступать к выполнению контрольного задания, не решив достаточного количества задач по материалу, соответствующему этому заданию; опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.

• Каждую контрольную работу следует выполнять в отдельной тетради.

• На обложке тетради должны быть написаны фамилия студента, его инициалы, номер зачетной книжки (шифр), название дисциплины, номер контрольной работы. В конце работы поставить дату выполнения.

• Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой учебного номера (шифра) зачетной книжки. Контрольные работы, выполненные не по своему варианту, не зачитываются.

• В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту.

• Перед решением задач надо полностью выписать их условия.

• Решение задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач.

• Все вычисления должны быть приведены полностью, чертежи и графики выполнены аккуратно, четко, с указанием единиц масштаба, координатных осей.

• Контрольная работа должна быть выслана на проверку не позднее, чем за две недели до начала экзаменационной сессии.

• После получения прорецензированной работы студент должен исправить в ней ошибки (сделать работу над ошибками в той же тетради). В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.

• При сдаче зачета или экзамена студент должен предоставить преподавателю-экзаменатору зачтенные работы.

Рабочая программа дисциплины «математика»

1. ОСНОВНЫЕ ПОНЯТИЯ ЛИНЕЙНОЙ АЛГЕБРЫ И ГЕОМЕТРИИ

1. Матрицы. Действия над матрицами.

2. Определители второго и третьего порядков, их свойства.

3. Миноры и алгебраические дополнения. Вычисление определителей разложением по элементам строки и столбца.

4. Системы линейных алгебраических уравнений, их решение: а) по формулам Крамера; б) методом Гаусса.

5. Прямоугольная система координат на плоскости и в пространстве. Задачи на метод координат.

6. Уравнение линии на плоскости. Различные виды уравнений прямой. Условие параллельности и перпендикулярности прямых.

7. Кривые второго порядка: окружность, эллипс, гипербола, парабола.

8. Векторы, линейные операции над векторами.

9. Скалярное произведение векторов и его свойства. Условия коллинеарности и ортогональности векторов.

10. Понятие векторного пространства. Линейная зависимость векторов. Разложение вектора по базису.

2. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

1. Элементы теории множеств, операции над множествами.

2. Функция, способы задания, свойства. Графики элементарных функций.

3. Упорядоченная переменная, ее предел. Следствия из определения предела.

4. Бесконечно малые и бесконечно большие величины, их свойства.

5. Теоремы о пределах.

6. Предел функции. Односторонние пределы.

7. Число е. Натуральные логарифмы. Замечательные пределы.

8. Вычисление пределов функций. Раскрытие неопределенностей.

9. Непрерывность функции в точке и на интервале. Точки разрыва, их классификация.

10. Непрерывность элементарных функций.

11. Сложная функция, ее непрерывность.

3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ В ИССЛЕДОВАНИИ ФУНКЦИЙ

1. Производная функции: определение, геометрический смысл производной.

2. Необходимое условие дифференцируемости функции.

3. Производная сложной функции.

4. Правила дифференцирования функций.

5. Таблица производных основных элементарных функций.

6. Понятие дифференциала функции, его применение.

7. Производные высших порядков.

8. Основные теоремы дифференциального исчисления: Ролля, Лагранжа.

9. Правило Лопиталя.

10. Определение возрастающей и убывающей функции, примеры. Достаточный признак монотонности функции.

11. Экстремум функции. Необходимое и достаточное условия существования экстремума.

12. Наибольшее и наименьшее значения функции y=f(x) на отрезке [a, b].

13. Выпуклость, вогнутость, точки перегиба графика функции.

14. Асимптоты графика функции.

15. Общая схема исследования и построения графика функции.

4. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ (ФНП)

1. Определение функции двух переменных. Геометрический смысл.

2. Предел и непрерывность ФНП.

3. Частные производные первого порядка функции z=f(x ,y).

4. Градиент.

5. Полное приращение и полный дифференциал функции z=f(x,y), их связь.

6. Частные производные высших порядков.

7. Локальный экстремум функции z=f(x,y). Необходимое условие существования экстремума функции z=f(x,y).

8. Условный экстремум.

9. Построение эмпирических формул по методу наименьших квадратов.

5. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

1. Первообразная и неопределенный интеграл.

2. Основные свойства неопределенного интеграла.

3. Таблица основных интегралов.

4. Основные методы интегрирования.

5. Определение определенного интеграла, геометрический и экономический смысл. Теорема существования определенного интеграла.

6. Свойства определенного интеграла.

7. Формула Ньютона – Лейбница. Вычисление определенных интегралов.

8. Метод подстановки.

9. Несобственные интегралы с бесконечными пределами.

10. Некоторые приложения определенного интеграла.

6. КОМПЛЕКСНЫЕ ЧИСЛА

1. Комплексные числа: определение, геометрическое изображение. Алгебраическая, тригонометрическая и показательная формы записи.

2. Действия над комплексными числами.

7. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (ДУ)

1. ДУ первого порядка. Общее и частное решения. Теорема существования.

2. ДУ первого порядка с разделяющимися переменными.

3. Линейные ДУ первого порядка.

4. ДУ второго порядка: основные понятия, ДУ вида .

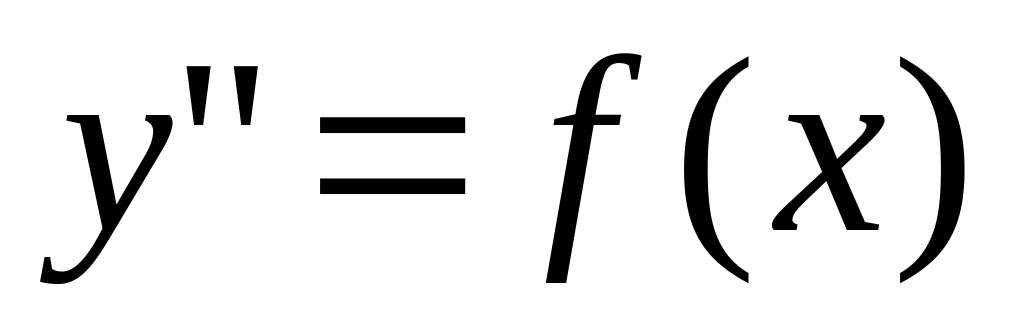5. Линейные ДУ второго порядка с постоянными коэффициентами: однородные и неоднородные.

8. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

1. Элементы комбинаторики: перестановки, размещения, сочетания.

   Семестр	№ КР	Содержание
   I	1	Основные понятия алгебры и геометрии
   	2	Введение в математический анализ. Производная
   	3	Приложения производной. Функции нескольких переменных.
   II	4	Неопределенный и определенный интегралы
   	5	Комплексные числа. Дифференциальные уравнения.
   	6	Теория вероятностей.

2. Виды событий. Классическое и статистическое определения вероятности.

3. Сумма событий. Теорема сложения вероятностей несовместных событий.

4. Произведение событий. Условная вероятность. Теоремы умножения вероятностей для независимых и зависимых событий.

5. Теорема сложения вероятностей совместных событий.

6. Схема независимых испытаний. Формула Бернулли.

7. Дискретная случайная величина (ДСВ), закон ее распределения. Биномиальное распределение.

8. Числовые характеристики ДСВ: математическое ожидание, дисперсия, их свойства.

9. Непрерывная случайная величина (НСВ): определение, пример.

10. Функция распределения, ее свойства.

11. Функция плотности вероятностей, свойства.