Механика
Раздел физики, который определяет самую простую форму движения материи – механическое|механичное| движение тел (изменение|смену| их положений в пространстве|просторе|).
Кинематика
Раздел механики, в котором|каком| описывается движение тел, но не анализируется его причины.
Основные понятия
Материальная точка – это тело, размеры которого можно не учитывать при данных условиях.
2
1 2
* *
1
а) б)
Траектория – линия в пространстве, вдоль которой двигается материальная точка (а – прямолинейное движение, б – криволинейный)
Перемещение - отрезок прямой, которая соединяет две точки траектории и направленный в сторону движения.
Путь (или l) - длина траектории (или ее участки).
Система отсчета (С.В.) – совокупность тела отсчета, системы координат и часов.
Тело отсчета может находиться|перебывать| в состоянии|стане| относительного покоя(а) или двигаться (б).
система
координат
ч
асы
в
в
в
тело
отсчета
Система
отсчета
а) б)
Равномерное прямолинейное движение
Это движение материальной точки вдоль| прямой с одинаковыми перемещениями|перемещением| в течение|на протяжении| любых|каких-нибудь| ровных|равных| промежутков времени.
Скорость
–
это отношение перемещения материальной
точки (
)
до времени (
),
за который оно состоялось. Скорость-вектор:
характеризует быстроту движения.
Используют также путейскую
скорость (скаляр)
.
Единицы
скорости:
.
Равномерное прямолинейное движение
Это движение материальной точки вдоль| прямой, в процессе которого|какого| влеченьем|поездом| любых|каких-нибудь| равных|равных| промежутков времени ее скорость изменяется одинаково.
Средняя скорость
|
Средняя скорость – скаляр
|
|
|
Среднюю скорость можно выразить как среднее арифметическое скоростей в начальный|первоначальный| и конечный|концевой| моменты времени.
Тогда
.
Мгновенная скорость – скорость за бесконечно малый промежуток времени.
На
примере путевой
скорости:
.
lim
(от
«limes»
или
–
«
limitis» -
предел);
- конечный прирост;
- бесконечно малый прирост.
(«´»| - символ|метка| производной)
Сложение|додает| скоростей
Часто тело принимает участие в нескольких независимых движениях. Скорость результирующего сложного движения равняется векторной сумме скоростей отдельных движений (добавление|додает| осуществляется по правилу параллелограмма или треугольника|трехугольника|).
Здесь:
.
Примеры|приклад|: движение красной смородине лодки с гребцом, движение самолета|самолет-торпедоносца| при сильном ветре, ходьба пассажира в вагоне|вагон-холодильнике|, который двигается.
Ускорение
В
случае разнообразного прямолинейного
движения для любого промежутка времени
ускорение равняется отношению изменения
скорости
(или
)
за этот промежуток к
(характеризует быстроту изменения
скорости).
При
этом
При этом
В
случае произвольно переменного
прямолинейного движения (при
)
рассматривают среднее и мгновенное
ускорение.
Средние величины
|
|
|
|
Мгновенные величины
|
|
|
|
Уравнение кинематики
равнопеременного|многообразного| прямолинейного движения
(при )
Записываются
с использованием скаляров
и
или проекций векторов
и
на ось абсцисс, направленную вдоль
траектории в сторону движения.
1.
,
2.
,
3.
.
Из|с| уравнения (3):
при
Графики зависимости
кинематических величин от времени
1. При
.
в s
б|б|
а
0 t 0 t
(Уравнение:
а)
б)
)
2. При
а
0 t 0 t
s
парабола
0
t
Равномерное криволинейное движение
1. Траектория – произвольная кривая.
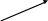
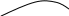
А В С
(мгновенная скорость направлена вдоль| касательной)
2. Траектория – круг|окружность|.
В процессе равномерного движения по кругу|окружности| материальная точка за любые|какие-нибудь| ровные|равные| промежутки времени проходит одинаковые пути по дуге этого круга|окружности|.
Характеристики движения материальной точки по кругу|окружности|
(или вращение тела)
Период
- время одного обхода круга материальной
точкой:
,
где
- число обходов за время
.
Частота
вращения тела
- число вращения тела за единицу времени:
.
0
касательная
Всюду
ускорение
перпендикулярное к касательной
(направлено по нормали
к ней), потому называется нормальным
ускорением
;
это ускорение направлено к
центру
круга,
потому называется также центростремительным
ускорением
- линейная скорость.
Линейная
скорость – скаляр
.
При
=1
путь равняется длине круга, время
равняется периоду
,
.
Угловая
скорость
.
.
При
радиус
описывает
угол
и возвращается в исходное положение.
.
Связь
линейной и угловой скоростей
.
Центростремительное нормальное ускорение:
.
Движение тела, брошенного|брошеного| под углом к|до| горизонту
в
парабола
h
0
а x
(сопротивление воздуха не учтено)
Высота
подъема
.
Дальность
полета
.
Время
полета
.
(
-
ускорение свободного падения).