
- •Тема 1. Степенева функція.
- •Означення кореня степеня
- •Властивості кореня степеня
- •С хема розв’язання рівняння виду:
- •Перетворення виразів з коренями
- •Внесення множника під знак кореня:
- •Винесення множника з-під знака кореня:
- •Означення степеня з раціональним показником
- •Тема 2. Ірраціональні рівняння.
- •Тема 3. Показникова функція. Показникові рівняння.
- •1. Функція виду , де , називається показниковою функцією.
- •2. Рівняння виду , де , називають найпростішим показниковим рівнянням.
- •1) Розв`язання показникових рівнянь зведенням до однієї основи
- •Зверніть увагу!
- •3) Розв`язання показнкових рівнянь, що зводяться до квадратних рівнянь
- •Зверніть увагу!
- •4) Розв`язання однорідних показникових рівнянь
- •Зверніть увагу!
- •Тема 4 . Показникові нерівності.
- •Зверніть увагу!
- •Вправи для самостійного розв’язування до теми 4:
- •Тема 5. Логарифм числа. Логарифмічна функція. Логарифмічні рівняння.
- •1. Означення логарифма
- •2. Властивості логарифмів
- •3. Логарифмічна функція
- •4. Орієнтир знаходження одз логарифмічної функції
- •5. Логарифмічні рівняння
- •Тема 6. Логарифмічні нерівності.
- •Т ема 7. Тригонометричні перетворення
- •Графіки тригонометричних функцій
- •Зверніть увагу! Завдання на використання формул 3 двійок риклад
- •Зверніть увагу!
- •Тема 8. Тригонометричні рівняння
- •Зверніть увагу!
- •Тема 9. Похідна функції
- •Обов`язково
- •Запам`ятайте!!!
- •Тема 10. Застосування похідної до дослідження функції
- •Дослідження функції на монотонність:
- •6. Схема дослідження функції для побудови її графіка:
- •Тема 11. Первісна. Невизначений інтеграл.
- •Зверніть увагу!
- •Тема 12. Визначений інтеграл.
- •Обчислення визначеного інтеграла
- •Основні властивості визначеного інтеграла
- •3. Геометричний зміст визначеного інтеграла
- •Фізичний зміст інтеграла
- •Обчислення об’ємів тіл
- •Вправи для самостійного розв’язування до теми 12:
- •1. Обчислити за допомогою формули Ньютона Лейбніца інтеграли.
- •2. Обчислити площу фігури, обмеженої лініями:
Тема 6. Логарифмічні нерівності.
При розв’язуванні логарифмічних нерівностей треба враховувати:
- властивості лінійних нерівностей;
- властивості монотонності логарифмічної функції та область її визначення.
Схема розв’язування найпростіших логарифмічних нерівностей
1 |
Якщо |
Якщо |
|
знак нерівності зберігається |
знак нерівності змінюється на протилежний |
2 |
Якщо |
Якщо |
|
знак нерівності зберігається |
знак нерівності змінюється на протилежний |
Приклад 1
Розв’язати нерівність:
 ОДЗ:
ОДЗ:






В раховуючи ОДЗ, маємо:

(16;
 )
0 16
)
0 16
Відповідь: (16; )
Приклад 2
Розв’язати нерівність:
 ОДЗ:
ОДЗ:



4
Враховуючи ОДЗ, маємо:
0 4
Відповідь:

Приклад 3
Розв’язати нерівність:
 ОДЗ:
ОДЗ:


Враховуючи властивість логарифмічної функції, маємо:





З врахуванням ОДЗ, маємо:
0 1000
Відповідь:

Приклад 4
Розв’язати нерівність:
 ОДЗ:
ОДЗ:





Враховуючи ОДЗ, маємо:
0
Відповідь:

Приклад 5
Розв’язати нерівність:
 ОДЗ:
ОДЗ:

 1
1

-1
0
Відповідь: (0; )
Приклад 6
Розв’язати нерівність:
 ОДЗ:
ОДЗ:
2
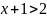
-1
1
Відповідь: (1; )
Приклад 7
Розв’язати нерівність:
 ОДЗ:
ОДЗ:
 2
2


-1
1
Враховуючи ОДЗ, маємо:
є (-1;1]
Відповідь: є (-1;1]
Приклад 8
Розв’язати нерівність:
 ОДЗ:
ОДЗ:


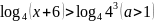


Враховуючи ОДЗ, маємо:
 -6
58
-6
58
Відповідь :
Приклад 9
Розв’язати нерівність:
 ОДЗ:
ОДЗ:
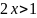





2
Враховуючи ОДЗ, маємо:
2
Відповідь:
Приклад 10
Розв’язати нерівність:





Відповідь:

Приклад 11
Розв’язати нерівність:


 ;
;



Відповідь :
Приклад 12
Розв’язати нерівність:
 ОДЗ
:
ОДЗ
:
Зробимо
заміну замінної:

Одержимо:

Р
 озв’яжемо
методом інтервалів:
озв’яжемо
методом інтервалів:

3
t

Повертаючись до заміни, маємо:



Враховуючи ОДЗ, маємо:











В


ідповідь:

Приклад 13
Розв’язати нерівність:
2
Зробимо заміну змінної:
 ,
,

Одержимо:

Розв’яжемо методом інтервалів:








Маємо:
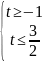 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

Враховуючи ОДЗ, маємо:
Відповідь
:

Вправи для самостійного розв’язування до теми 6:
Розв’яжіть
нерівність:
1) 10)
10)
 2)
2)
 11)
11)
3) ; 12)
; 12)
 ;
4)
;
4) ;
13)
;
13)

5) ;
14)
;
14)
6)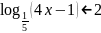 ;
15)
;
15) ;
;
7)
 ;
16)
;
16) 8)
8) ;
17)
;
17)
9)
 ; 18)
; 18)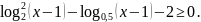


 ,
тоді
,
тоді
 ,
тоді
,
тоді
 ,
тоді
,
тоді ,
тоді
,
тоді