1) Розв`язання показникових рівнянь зведенням до однієї основи

Схема розв`язання:

1. Перетворити ліву та праву частини рівняння до вигляду степеня з однією основною але з різними показниками.

,

2. Якщо рівні основи степеня , тоді рівні їх показники, тобто

Приклади. Розв`язати рівняння:

1. = 49 ; 2) ; 3) = 4) = 1

=7² =7^-1 = =7⁰

=

Відповідь : Відповідь: Відповідь: Відповідь:

5) 6)

Оскільки завжди Оскільки завжди

Відповідь : коренів не має Відповідь : коренів не має

7)

Поділимо обидві частини рівняння на вираз ( > 0).

Отримаємо:

Зверніть увагу!

;

Відповідь: 0

8

Зверніть увагу!

)

2

Відповідь: 2.

9

Зверніть увагу!

)

Відповідь:

1

Зверніть увагу!

0)

Відповідь:

Зверніть увагу!

11) (3,5

Відповідь: 1

12) (0,5 16 ; 13) ( ^-1 1 ;

; ;

2⁴ ; ;

; ;

. .

Відповідь 2 Відповідь: 2; 1.

1

Зверніть увагу!

0,125

4) 0,125 4;

2^-3 2² ;

2²

;

;

Відповідь:

2) Розв`язання показникових рівнянь за допомогою розкладання однієї з частин на множники (винесення степеня з найменшим показником, коефіцієнти показників цих степенів набувають однакових значень).

Схема розв`язання:

1) Звести всі степені до однієї основи.

2) Винести за дужки степінь із найменшим показником.

У такому випадку в дужках завжди утворюється числовий вираз

без змінної .

3) Перетворити рівняння до найпростішого показникового рівняння

та розв`язати його.

Приклади.

Розв`язати рівняння:

1)

За дужки винесемо степінь з найменшим показником

(7+4) 539; 1)

11 539 ; 2)

739:11

49;

7²;

;

Відповідь: 1.

2. 

За дужки винесемо степінь з найменшим показником.

1) 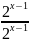=1

2)

;

;

;

2²

;

Відповідь: 3

3) 704

За дужки винесемо степінь з найменшим показником.

(2³+2² 1) 704; 1) =2^х-4-(х-7) 2^х-4-х+7 2³

(8+4 1) 704 ; 2)

11 704 ; 3) 1

704:11 ;

64 ;

2⁶ ;

Відповідь: 13