
- •Тема 1. Степенева функція.
- •Означення кореня степеня
- •Властивості кореня степеня
- •С хема розв’язання рівняння виду:
- •Перетворення виразів з коренями
- •Внесення множника під знак кореня:
- •Винесення множника з-під знака кореня:
- •Означення степеня з раціональним показником
- •Тема 2. Ірраціональні рівняння.
- •Тема 3. Показникова функція. Показникові рівняння.
- •1. Функція виду , де , називається показниковою функцією.
- •2. Рівняння виду , де , називають найпростішим показниковим рівнянням.
- •1) Розв`язання показникових рівнянь зведенням до однієї основи
- •Зверніть увагу!
- •3) Розв`язання показнкових рівнянь, що зводяться до квадратних рівнянь
- •Зверніть увагу!
- •4) Розв`язання однорідних показникових рівнянь
- •Зверніть увагу!
- •Тема 4 . Показникові нерівності.
- •Зверніть увагу!
- •Вправи для самостійного розв’язування до теми 4:
- •Тема 5. Логарифм числа. Логарифмічна функція. Логарифмічні рівняння.
- •1. Означення логарифма
- •2. Властивості логарифмів
- •3. Логарифмічна функція
- •4. Орієнтир знаходження одз логарифмічної функції
- •5. Логарифмічні рівняння
- •Тема 6. Логарифмічні нерівності.
- •Т ема 7. Тригонометричні перетворення
- •Графіки тригонометричних функцій
- •Зверніть увагу! Завдання на використання формул 3 двійок риклад
- •Зверніть увагу!
- •Тема 8. Тригонометричні рівняння
- •Зверніть увагу!
- •Тема 9. Похідна функції
- •Обов`язково
- •Запам`ятайте!!!
- •Тема 10. Застосування похідної до дослідження функції
- •Дослідження функції на монотонність:
- •6. Схема дослідження функції для побудови її графіка:
- •Тема 11. Первісна. Невизначений інтеграл.
- •Зверніть увагу!
- •Тема 12. Визначений інтеграл.
- •Обчислення визначеного інтеграла
- •Основні властивості визначеного інтеграла
- •3. Геометричний зміст визначеного інтеграла
- •Фізичний зміст інтеграла
- •Обчислення об’ємів тіл
- •Вправи для самостійного розв’язування до теми 12:
- •1. Обчислити за допомогою формули Ньютона Лейбніца інтеграли.
- •2. Обчислити площу фігури, обмеженої лініями:
Тема 11. Первісна. Невизначений інтеграл.
1. Означення первісної.
Функція
 називається первісною
для функції
на заданому проміжну, якщо для всіх
із цього проміжку виконується рівність
називається первісною
для функції
на заданому проміжну, якщо для всіх
із цього проміжку виконується рівність

2. Основна властивість первісної
Якщо
 первісна для функції
на заданому проміжку, то функція
має безліч первісних, і всіх їх можна
задати формулою
первісна для функції
на заданому проміжку, то функція
має безліч первісних, і всіх їх можна
задати формулою
 ,
де
,
де
 довільне число.
довільне число.
Наприклад,
для функції

 первісними є функції
первісними є функції
 ,
або
,
або
 ,або
,або
 і взагалі
і взагалі
 ,
де
довільне число
,
де
довільне число
Оскільки
 ,
або
,
або

3. Геометричний зміст первісних
Г
 рафіки
будь-яких первісних для даної функції
одержуються один з одного паралельним
перенесенням уздовж осі 0у
рафіки
будь-яких первісних для даної функції
одержуються один з одного паралельним
перенесенням уздовж осі 0у

4. Означення невизначеного інтегралу
Сукупність усіх первісних для функції називають невизначеним інтегралом функції і позначають
 ,
де
,
де
 підінтегральна
функція
підінтегральна
функція
 підінтегральний
вираз
підінтегральний
вираз
одна з первісних для функції
довільне число

 -1
-1
5. Основні правила інтегрування
1.
 ;
;
2.
 ;
;
3.

Приклади . Знайти загальний вигляд первісної для функцій :
1)
 ;
;
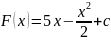 ;
;
2)

 ;
;
Зверніть увагу!
3)
 ;
;

 ;
;
4)
 ;
;
 ;
;
5)
 ;
;
 ;
;
 ;
;
6)
 ;
;
 .
.
2.
Для функції
знайдіть первісну
 ,
що набуває заданого значення :
,
що набуває заданого значення :
1)


За
умовою
 ,
тобто
,
тобто




Тобто

2)


За
умовою
 тобто
тобто
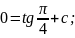


Тобто

3.
Для функції
 знайдіть первісну, графік якої проходить
через точку M(1;0)
знайдіть первісну, графік якої проходить
через точку M(1;0)


За умовою


 0
0
Тобто
 .
.
4. Знайти інтеграл :
1)




 ;
;
2)


 ;
;
3)

 ;
;
4)
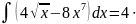
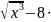


 ;
;
5)

 ;
;
6)










 ;
;
7)



 ;
;
8)



 ;
;
9)



 .
.
Вправи для самостійного розв’язування до теми 11:
1.
Знайдіть
загальний вигляд первісної для

1)
 2
2 7)
7)
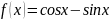 ;
;
2)
 ; 8)
; 8)
 ;
;
3)

 ; 9)
; 9)
 ;
;
4)
; 10)
 ;
;
5)
; 11)
 ;
;
6)
 ; 12)
; 12)

 .
.
2.
Для
функції
 знайдіть первісну , графік якої проходить
через точку
знайдіть первісну , графік якої проходить
через точку
 .
.
3. Для функції знайдіть первісну , що набуває заданого значення в зазначеній точці
1)
 ,
.
,
.
2)
 ,
,

3)
 ,
,
 .
.
4. Знайдіть невизначений інтеграл :
1)
 ;
;
2)
 ;
;
3)
 ;
;
4)
 ;
;
5)
 ;
;
6)
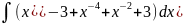 ;
;
7)
 ;
;
8)

9)
 ;
;
10)
 ;
;
11)
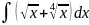 ;
;
12)
 ;
;
13)
 ;
;
14)
 ;
;
15)
 ;
;
16)
 ;
;
17)
 ;
;
18)
 ;
;
19)
 ;
;
20)
 ;
;
21)
 ;
;
22)
 .
.
