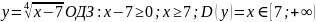- •Тема 1. Степенева функція.
- •Означення кореня степеня
- •Властивості кореня степеня
- •С хема розв’язання рівняння виду:
- •Перетворення виразів з коренями
- •Внесення множника під знак кореня:
- •Винесення множника з-під знака кореня:
- •Означення степеня з раціональним показником
- •Тема 2. Ірраціональні рівняння.
- •Тема 3. Показникова функція. Показникові рівняння.
- •1. Функція виду , де , називається показниковою функцією.
- •2. Рівняння виду , де , називають найпростішим показниковим рівнянням.
- •1) Розв`язання показникових рівнянь зведенням до однієї основи
- •Зверніть увагу!
- •3) Розв`язання показнкових рівнянь, що зводяться до квадратних рівнянь
- •Зверніть увагу!
- •4) Розв`язання однорідних показникових рівнянь
- •Зверніть увагу!
- •Тема 4 . Показникові нерівності.
- •Зверніть увагу!
- •Вправи для самостійного розв’язування до теми 4:
- •Тема 5. Логарифм числа. Логарифмічна функція. Логарифмічні рівняння.
- •1. Означення логарифма
- •2. Властивості логарифмів
- •3. Логарифмічна функція
- •4. Орієнтир знаходження одз логарифмічної функції
- •5. Логарифмічні рівняння
- •Тема 6. Логарифмічні нерівності.
- •Т ема 7. Тригонометричні перетворення
- •Графіки тригонометричних функцій
- •Зверніть увагу! Завдання на використання формул 3 двійок риклад
- •Зверніть увагу!
- •Тема 8. Тригонометричні рівняння
- •Зверніть увагу!
- •Тема 9. Похідна функції
- •Обов`язково
- •Запам`ятайте!!!
- •Тема 10. Застосування похідної до дослідження функції
- •Дослідження функції на монотонність:
- •6. Схема дослідження функції для побудови її графіка:
- •Тема 11. Первісна. Невизначений інтеграл.
- •Зверніть увагу!
- •Тема 12. Визначений інтеграл.
- •Обчислення визначеного інтеграла
- •Основні властивості визначеного інтеграла
- •3. Геометричний зміст визначеного інтеграла
- •Фізичний зміст інтеграла
- •Обчислення об’ємів тіл
- •Вправи для самостійного розв’язування до теми 12:
- •1. Обчислити за допомогою формули Ньютона Лейбніца інтеграли.
- •2. Обчислити площу фігури, обмеженої лініями:
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ОДЕСЬКЕ МОРЕХІДНЕ УЧИЛИЩЕ РИБНОЇ ПРОМИСЛОВОСТІ
ІМЕНІ ОЛЕКСІЯ СОЛЯНИКА
Методичні рекомендації
до вивчення дисципліни «Математика»
загальноосвітнього циклу
Одеса 2015
Укладач : Н. Г. Тушкова , викладач математики I категорії
ОМУ РП імені О. Соляника
Методичні рекомендації розглянуті й ухвалені на засіданні циклової комісії фундаментальних дисциплін загальноосвітньої підготовки
Протокол №______ від _________2015 р.
Голова циклової комісії фундаментальних дисциплін загальноосвітньої
підготовки ______________ /Л. П. Федячкіна/
Методичні рекомендації розглянуті й затверджені на засіданні методичної ради ОМУ РП ім. О. Соляника й рекомендовані для використання під час підготовки до занять , самостійної та контрольної роботи , державної підсумкової атестації.
Протокол №______ від _________2015 р.
Голова методичної ради _____________ /Н. А. Мельник/
Вступ
Методичні рекомендації до розв`язання вправ з алгебри та початків аналізу складено відповідно до навчальної програми дисципліни «Математика» і розроблено з метою надання методичної допомоги курсантам 1 курсу денної форми навчання для засвоєння теоретичних знань та практичних вмінь.
У методичних рекомендаціях логічно впорядковано та систематизовано основні поняття з тем : «Степенева функція», «Показникова функція» , «Логарифмічна функція», «Тригонометрична функція» , «Похідна та її застосування» та «Первісна та інтеграл».
Методичні рекомендації містять практичні вправи для самостійного розв`язування , що сприяють засвоєнню , закріпленню пройденого матеріалу та перевірки отриманих знань.
Матеріали методичних рекомендацій допоможе знайти необхідну інформацію (означення, формули, приклади) ; згадати як розв`язуються типові завдання ; повторити та систематизувати відповідний матеріал під час підготовки до занять , контрольних робіт та державної підсумкової атестації.
Тема 1. Степенева функція.
Означення кореня степеня
Коренем
степеня
з числа
 називають
таке число
називають
таке число
 степінь
якого дорівнює числу
степінь
якого дорівнює числу
 , якщо
, якщо


 – показник
степеня
– підкореневий вираз
– показник
степеня
– підкореневий вираз
Наприклад:




Властивості кореня степеня
|
|
|
|
1)
2) 3) 4) 5) |
|
Таблиця коренів
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад 1. Спростити :

С хема розв’язання рівняння виду:

|
|
||
При
будь-яких значеннях
рівняння
має єдиний корінь
|
При
коренів не має |
При
має єдиний корінь
|
При
два кореня
|
Розв`язати рівняння:
Відповідь: |
Розв’язати рівняння:
Відповідь: рівняння коренів не має |
Розв’язати рівняння:
Відповідь: 0 |
Розв’язати рівняння :
Відповідь |
Перетворення виразів з коренями
Внесення множника під знак кореня:
 ;
; .
.
Винесення множника з-під знака кореня:
 або
-
непарне
;
або
-
непарне
; .
.
Приклад 2. Винести множник з-під знака кореня :
 ;
; ;
; ;
; ;
;
Приклад 3. Внести множник під знак кореня :
 ;
; ;
; .
.
Приклад 4. Спростити вираз:
 ;
;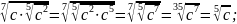
 .
.
Означення степеня з раціональним показником
С ,
представленим у вигляді
,
представленим у вигляді
 ,
де
,
де
 називається число
називається число
 тобто
тобто

Приклад:



Функція
виду
 ,
де
,
де
 – будь-яке дійсне число, називається
степеневою функцією.
– будь-яке дійсне число, називається
степеневою функцією.




 ,
,

 ,
,



 ,
,

 ,
,



 ,
,
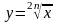
 ,
,

Приклад 5. Спростіть дріб:
Зверніть увагу!
|
Зверніть увагу!
|
 ;
; .
.
Приклад 6. Спростіть дріб:
Зверніть увагу!
|
Зверніть увагу!
|
 ;
; ;
;

Приклад 7. Знайдіть область визначення функції :





Приклад 8. Знайдіть область визначення функції :
Вправи для самостійного розв’язування до теми 1:
Знайдіть значення виразу:
 ;
; ;
; ;
; +
+ ;
; +
+ .
.
Спростіть вираз:
 ; 2)
; 2)
 ;
3)
;
3)
 4)
4)
 ;
5)
;
5)
 .
.
Знайдіть область визначення функції:
 ;
5) y
=
;
5) y
=
 ;
; ;
6) y
=
;
6) y
= ;
; ;
7) y
=
;
7) y
= ;
; ; 8)
y
=
; 8)
y
= .
.
Розв’яжіть рівняння:
1)
 ;
5)
;
5)
 ;
;
2)
 ;
6)
;
6)
 ;
;
3)
 ;
7)
;
7)
 ;
;
4)
 ;
8)
;
8)
 .
.
Винесіть множник з-під знака кореня:
1)
 ;
4)
;
4)
 ;
;
2)
 ;
5)
;
5)
 ;
;
3)

 ;
6)
;
6)

Внесіть множник під знак кореня:
 ;
2)
;
2)
 ;
3)
3
;
3)
3 ;
4)
;
4)
 .
.
Скоротіть дріб:
 ;
6)
;
6)
 ;
; ;
7)
;
7)


 ;
8)
;
8)

 ;
; .
.
Знайдіть значення виразу:
 ;
2)
;
2)
 ;
3)
;
3)
 ; 4)
; 4)
 .
.
Знайдіть область визначення функції:
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
Знайдіть значення виразу:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
;
4)
 .
.
Знайдіт значення виразу:
 ; 2)
; 2)
 ;
3)
;
3)
 ;
;
4)
 ; 5)
; 5)
 ; 6)
; 6)
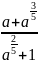 .
.



 існує
при будь -якому
значенні
існує
при будь -якому
значенні


 існує
тільки при
існує
тільки при














 =
2
=
2














 2
2



 -
непарне
число
-
непарне
число
 парне
число
парне
число

 рівняння
рівняння рівняння
рівняння
 рівняння
має
рівняння
має

 ;
; ;
;



 ;
; ;
; ;
; ;
;
 2;
2
2;
2