МИНИCTEPCTBO ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«СЕВЕРО-КАВКАЗСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт сервиса, туризма и дизайна (филиал) СКФУ в г. Пятигорске
Отчёт по лабораторной работе
По дисциплине
Теория Автоматического Управления
Тема:
«Анализ линейных систем автоматического регулирования»
Выполнил:
Студент группы УТС-141
Инженерного Факультета
Шевцов М. М.
Пятигорск 2016.
ЦЕЛЬ РАБОТЫ:
Изучить методы анализа линейных систем автоматического управления.
ЗАДАНИЕ ПО ЛАБОРАТОРНОЙ РАБОТЕ ·
Ознакомиться с методами анализа линейных систем автоматического управления; ·
Применить изученные методы на конкретном примере;
Исходные данные к лабораторной работе
Для объекта, передаточная функция которого описывается в виде:
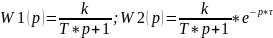
где p – оператор Лапласа.
Коэффициент передачи k = 123,5;
Постоянная времени апериодического звена T = 2.405;
Постоянная времени звена чистого запаздывания τ= 0.546;
W |
b |
a |
20LogM |
Ф |
LogW |
M |
0,004158 |
-1,23488 |
123,4877 |
41,83247 |
-0,01 |
-2,38112 |
123,4777 |
0,044158 |
-12,9694 |
122,1226 |
41,73592 |
-0,1058 |
-1,35499 |
122,0164 |
0,064158 |
-18,6129 |
120,628 |
41,62896 |
-0,15309 |
-1,19275 |
120,4736 |
0,084158 |
-24,0127 |
118,6398 |
41,48461 |
-0,1997 |
-1,0749 |
118,4373 |
0,104158 |
-29,1101 |
116,2079 |
41,30471 |
-0,24545 |
-0,98231 |
115,9572 |
0,124158 |
-33,8582 |
113,3899 |
41,09149 |
-0,29017 |
-0,90603 |
113,0909 |
0,144158 |
-38,223 |
110,2481 |
40,84742 |
-0,33373 |
-0,84116 |
109,9008 |
0,164158 |
-42,1829 |
106,8462 |
40,57518 |
-0,37602 |
-0,78474 |
106,4507 |
0,184158 |
-45,7281 |
103,247 |
40,27755 |
-0,41693 |
-0,73481 |
102,8032 |
0,204158 |
-48,8594 |
99,51002 |
41,83247 |
-0,01 |
-2,38112 |
123,4777 |
A
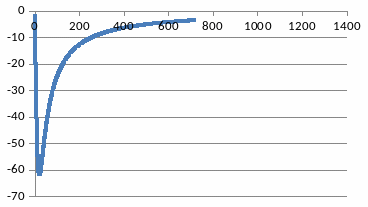
20LogM
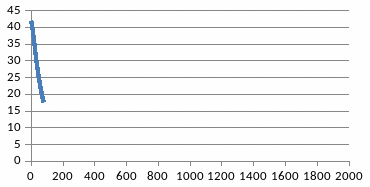
Φ
W |
A |
B |
M |
F |
20LogM |
logW |
0,004158 |
123,4845 |
-1,51522 |
123,4938 |
-0,01227 |
41,8329 |
-2,38112 |
0,024158 |
122,9795 |
-8,77406 |
123,2921 |
-0,07123 |
41,8187 |
-1,61694 |
0,044158 |
121,7745 |
-15,9098 |
122,8094 |
-0,12991 |
41,78463 |
-1,35499 |
0,064158 |
119,9021 |
-22,8263 |
122,0556 |
-0,18812 |
41,73115 |
-1,19275 |
0,084158 |
117,4116 |
-29,437 |
121,0455 |
-0,24565 |
41,65897 |
-1,0749 |
0,104158 |
114,3654 |
-35,6682 |
119,7985 |
-0,30232 |
41,56903 |
-0,98231 |
0,124158 |
110,836 |
-41,4613 |
118,337 |
-0,35796 |
41,46241 |
-0,90603 |
0,144158 |
106,9013 |
-46,7734 |
116,6861 |
-0,41244 |
41,34038 |
-0,84116 |
0,164158 |
102,6415 |
-51,5774 |
114,8717 |
-0,46565 |
41,20426 |
-0,78474 |
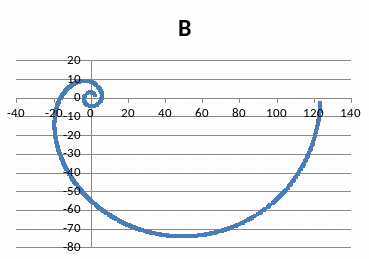
ЗАКЛЮЧЕНИЕ И ВЫВОДЫ:
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________