17.2 Перетворення енергії в коливальному контурі. Виведення диференціального рівняння власних коливань. Формула Томсона

Перетворення енергії в коливальному контурі

Роздивимося рисунок 17.5.

Рисунок 17.5, 1) у момент часу t = 0 заряджають конденсатор – у середині конденсатора утворюється електричне поле з енергією W_Cmax.

Рисунок 17.5, 2) протягом часу від 0 до Т/8 конденсатор розряджається через котушку. У котушці з’являється електричний струм, який створює магнітне поле в котушці. Сила струму в котушці не наростає миттєво, оскільки йому протидіє ЕРС самоіндукції.

Таким чином енергія електричного поля конденсатора W_C поступово переходить в енергію магнітного поля котушки W_L.

Рисунок 17.5 3) у момент часу t = Т/4 конденсатор повністю розряджається. Напруга на ньому відсутня. Але внаслідок явища самоіндукції, через котушку тече максимальний струм І₀. Тобто вся енергія електричного поля конденсатора W_Cmax перетворилася в енергію магнітного поля котушки W_Lmax. Далі сила струму в котушці починає зменшуватися, але його миттєвому зменшенню знову-таки протидіє ЕРС самоіндукції. Тобто тепер котушка відіграє роль джерела електричного струму, що заряджає конденсатор до початкового заряду; при цьому знак заряду на пластинах конденсатора стає протилежним попередньому.

Рисунок 17.5 4) у момент часу t = Т/2 вся енергія магнітного поля котушки перетворилася на енергію електричного поля конденсатора.

Далі процес повторюється.

Таким чином, для електромагнітних коливань виконується закон збереження енергії. W_Cmax = W_L + W_C = W_Lmax;

.

Формула Томсона

1. Період електромагнітних коливань залежить від індуктивності й ємності коливального контуру.

2. Визначення. Період власних електромагнітних коливань – це час одного повного електромагнітного коливання в коливальному контурі.

3. Період власних електромагнітних коливань – це скалярна величина.

4. 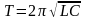, де L – індуктивність котушки контуру; С – ємність конденсатора контуру. Ця формула дістала назву формули Томсона, на честь видатного англійського фізика У. Томсона, який отримав її вперше.

5. [T] = с (Секунда).

17.3 Диференціальне рівняння затухаючих електричних коливань та його розв’язок. Вимушені електричні коливання, їх диференціальне рівняння

Диференціальне рівняння затухаючих електричних коливань та його розв’язок.

У реальному контурі мають місце такі втрати енергії:

1) теплові втрати, оскільки R≠0;

2) втрати в діелектрику конденсатора;

3) гістерезисні втрати в осерді котушки;

4) втрати на випромінювання та інше.

Через ці втрати коливання затухають.

Диференціальне рівняння затухаючих електричних коливань має вигляд:

, а його розв’язок .

У даних рівняннях q – заряд конденсатора коливального контуру, Q₀ – амплітуда заряду на початку затухаючих коливань, - коефіцієнт затухання, - циклічна частота затухаючих коливань, φ₀ – початкова фаза коливань..

Вимушені електричні коливання, їх диференціальне рівняння.

1. Якщо розглядати коливальний контур, то для отримання вимушених коливань потрібно включити послідовно з елементами контуру змінну ЕРС або, розірвавши контур, подати змінну напругу U=U₀cos.

2. Визначення. Вимушені електричні коливання – це електричні коливання, які виникають під дією змінної ЕРС.

3. Умови виникнення: а) існування коливального контуру; б) наявність джерела змінного струму, приєднаного до контуру.

4. Диференціальне рівняння вимушених коливань в коливальному контурі має вигляд: , розв’язок цього рівняння такий

.

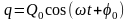У даних рівняннях q – заряд конденсатора коливального контуру, - коефіцієнт затухання, Q₀ – амплітуда заряду вимушених коливань, - циклічна частота вимушених коливань, φ₀ – початкова фаза коливань, U₀ – амплітуда напруги вимушених коливань, L - індуктивність коливального контуру.

5 . Пояснення явища. Від джерела змінної ЕРС у коливальний контур безперервно надходить енергія, миттєва потужність якої p=iu. У початковий момент енергія, що надходить у коливальний контур, частково перетвориться в енергію коливань, що виникають у контурі, а частково необоротно перетвориться в тепло, що розсіюється в просторі. Миттєва потужність, необоротно перетвореної в тепло енергії, дорівнює p_q=i²R. Під час збільшення амплітуди електромагнітних коливань збільшується величина сили струму в контурі. Зі збільшенням струму зростає енергія, що надходить у контур, й енергія, яка необоротно перетворена в тепло. На рисунку 17.6 приведені графіки зміни миттєвої потужності енергії, що надходить у контур (р), і потужності необоротно перетвореної енергії (p_q). Тому що миттєва потужність енергії, що надходить у контур, пропорційна силі струму, а потужність необоротно перетвореної енергії пропорційна квадрату сили струму, то в деякий момент часу вся енергія, що надходить у контур, буде необоротно перетворюватися в теплоту (точка В на рисунку 17.6), відтепер амплітуда коливань у контурі збільшуватися не буде. У контурі встановлюються стаціонарні вимушені коливання, частота яких дорівнює частоті змінної ЕРС.