16.5 Механічний резонанс. Добротність коливальної системи при резонансі
Явище механічного резонансу
1. Приклади явища. Резонанс досить часто людина спостерігає у повсякденному житті: це розгойдування гойдалки, трамбівка ґрунту, вимірювання частоти коливань за допомогою частотоміра.
2. Визначення. Різке зростання амплітуди коливань при співпаданні власної частоти коливальної системи з частотою дії періодичної зовнішньої сили називають резонансом. (від англійського слова resonans – той, що відгукується.)
3. Умови виникнення явища: а) наявність коливальної системи (будь-яке тіло внаслідок існування сил пружності є коливальною системою); б) наявність дії на коливальну систему періодичної зовнішньої сили; в) власна частота коливальної системи ω0 повинна співпадати з частотою дії зовнішньої періодичної сили ωF; г) при резонансі коливальна система отримує максимальну енергію від зовнішнього джерела; д) при зростанні сил тертя, що виникають у коливальній системі, амплітуда резонансних коливань зменшується. Так на рисунку 16.9 крива 1 відповідає коливальній системі з мінімальною силою тертя, а крива 3 – із максимальною.
4
.
Математичний опис. Якщо коефіцієнт
затухання β
= 0, то резонанс спостерігається на
частоті ω0
= ωF.
А амплітуда резонансних коливань
має вигляд
,
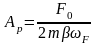й оскільки β
= 0 - йде в нескінченність, при цьому
енергія постійно вводиться в систему
й не розсіюється.
У реальних системах β ніколи не дорівнює 0, тому резонансний пік має кінцеву висоту, а резонансна частота ωр <ω0. Якщо коефіцієнт загасання β малий, то ω0 ≈ ωр. Якщо ж затухання велике, то пік виражений слабо або зовсім відсутній (крива 3 на рисунку 16.9).
Слід зазначити, що резонансна частота також залежить від коефіцієнту затухання, і чим більший коефіцієнт, тим менша резонансна частота.
5.
Пояснення явища. При резонансі зовнішня
сила діє в такт вільним коливанням, вона
напрямлена за напрямком швидкості й
виконує роботу по збільшенню енергії
коливальної системи протягом усього
періоду коливань. Тому енергія коливань
зростає, а значить і їхня амплітуда
також буде збільшуватися. Для пружинного
маятника це видно з формули
.
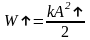Добротність коливальної системи при резонансі
1. Висота й ширина резонансного піку характеризуються параметром Q, який називається добротністю.
2. Визначення. Добротністю коливальної системи називають відношення резонансної амплітуди до статичного зміщення.
3. Це скалярна величина.
4.
,
де Ар
резонансна амплітуда,
Аст
- статичне зміщення.
*Статичне зміщення – це зміщення під дією сталої сили, яка за величиною рівна амплітудному значенню змінної сили F0, що викликає резонанс.
Практично
точно виміряти Аст
складно. Тому добротність знаходять за
графіком резонансної кривої (рис. 11) за
формулою
,
де Δω
різниця частот для амплітуди вимушених
коливань, яка відповідає значенню
.
5. [Q] = 1.
Запитання до лекції № 16
1. Дайте визначення гармонійного коливання, напишіть його рівняння.
2. Укажіть на зв'язок між повертаючою силою та зміщенням із положення рівноваги матеріальної точки, що гармонійно коливається.
3. Напишіть диференціальне рівняння гармонійного коливання матеріальної точки та вкажіть на його розв’язок.
4. Від чого залежить власна частота гармонійних коливань матеріальної точки? Напишіть відповідну формулу.
8. Які коливання в коливальному контурі називаються власними?
5. Напишіть формули, що визначають кінетичну, потенціальну та повну енергію матеріальної точки, що гармонійно коливається.
6. Покажіть гармонійне коливання за допомогою вектора.
7. Які коливання називаються вільними?
8. У якому випадку вільні коливання будуть власними?
9. Напишіть диференціальне рівняння вільних механічних коливань у середовищі з лінійним опором.
10. Напишіть рівняння вільних механічних коливань в середовищі з лінійним опором (рівняння механічних затухаючих коливань).
11. За якою формулою визначають циклічну (кругову) частоту механічних затухаючих коливань?
12. Як змінюється з часом амплітуда затухаючих коливань?
13. Дайте визначення логарифмічного коефіцієнта (декремента) затухання коливань та покажіть, як він зв’язаний із періодом.