Задача 4а (вариант с параметром).

Найти параметр , при котором ранг матрицы

равен 2.

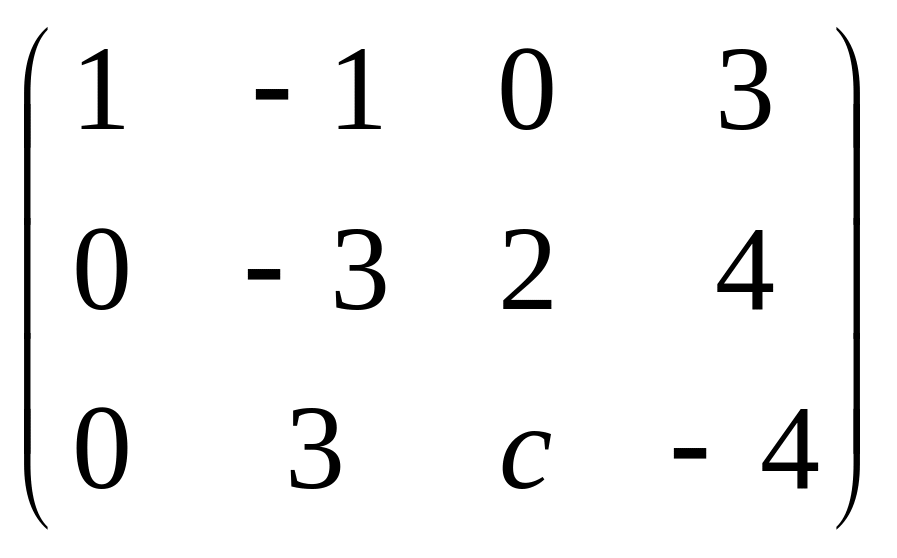
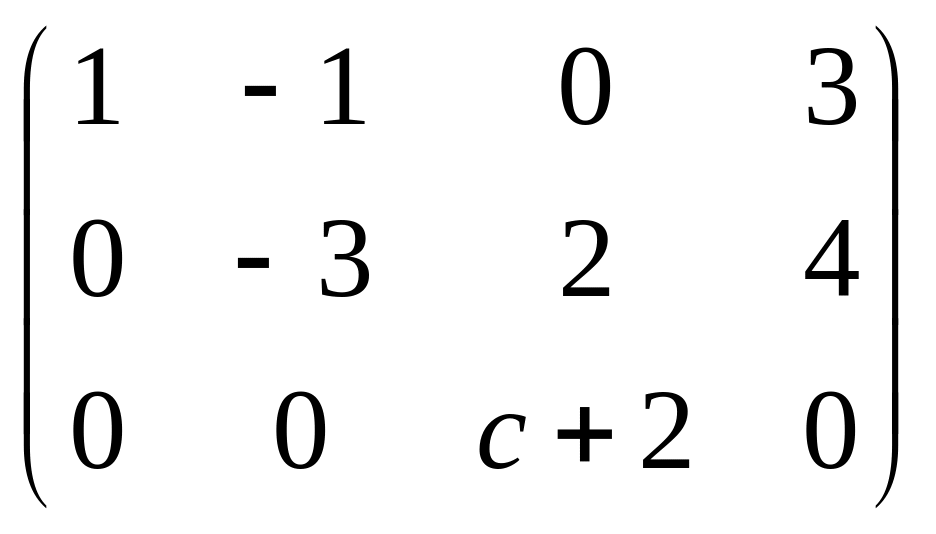
Третья строка сосотяла бы из всех нулей, только если , то есть . То есть, если бы на месте a₃₃ изначально было число -2, то ранг был бы меньше, так как в итоге получилась бы третья строка из всех нулей.

Ответ. .

Задача 5. Доказать, что 3 столбец матрицы

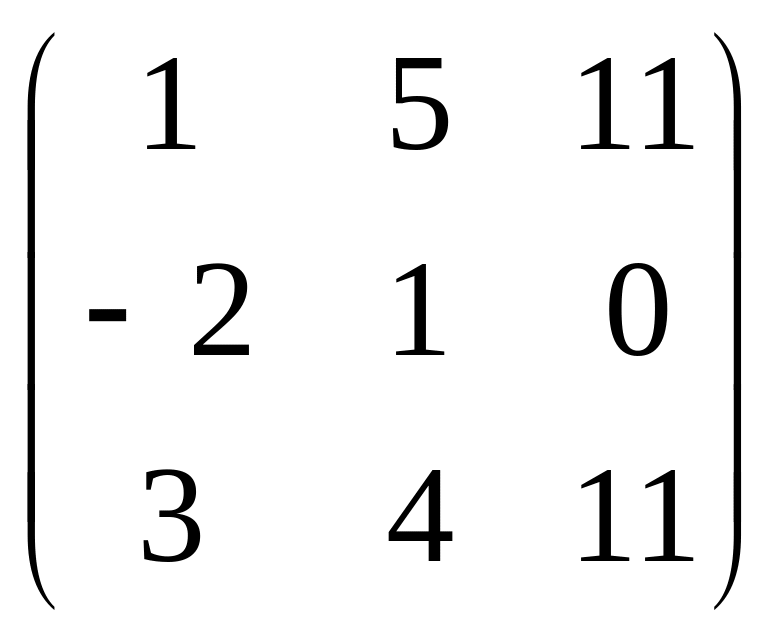
является линейной комбинацией первых двух, и найти коэффициенты этой комбинации.

Решение. Во-первых, если вычислить определитель и обнаружить, что он равен 0, то этим самым уже доказана линейная зависимость столбцов. Однако требуется найти коэффициенты, поэтому запишем систему уравнений:

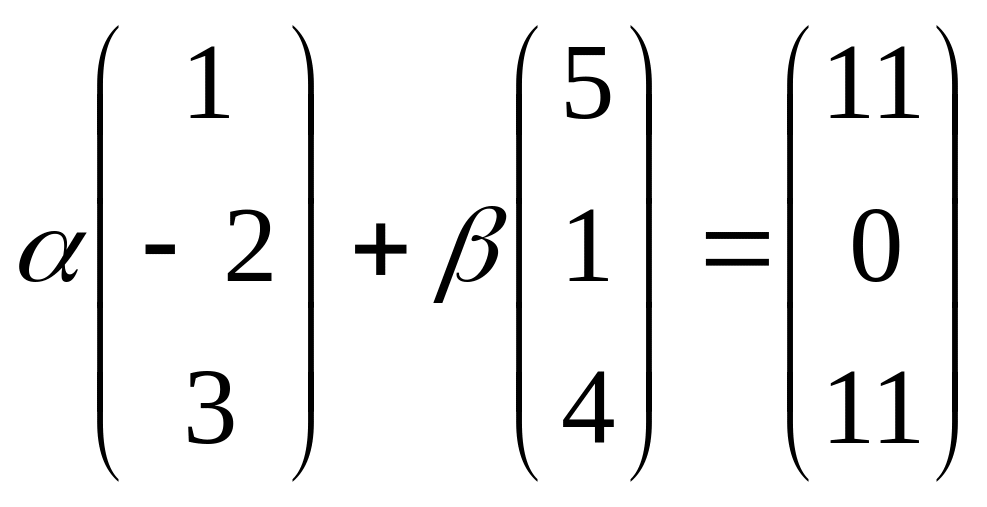
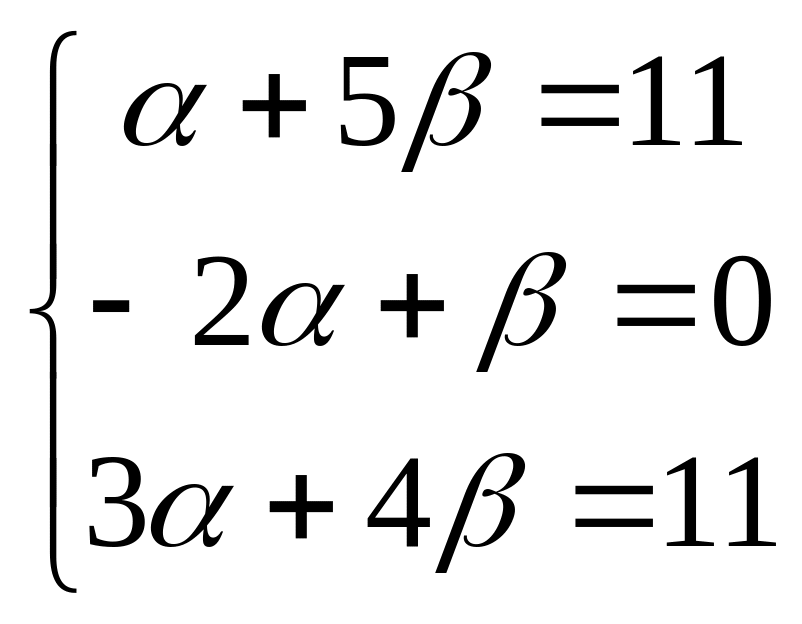
Прибавим удвоенное 1-е уравнение ко 2-му, и вычтем утроенное 1-е из 3-го.

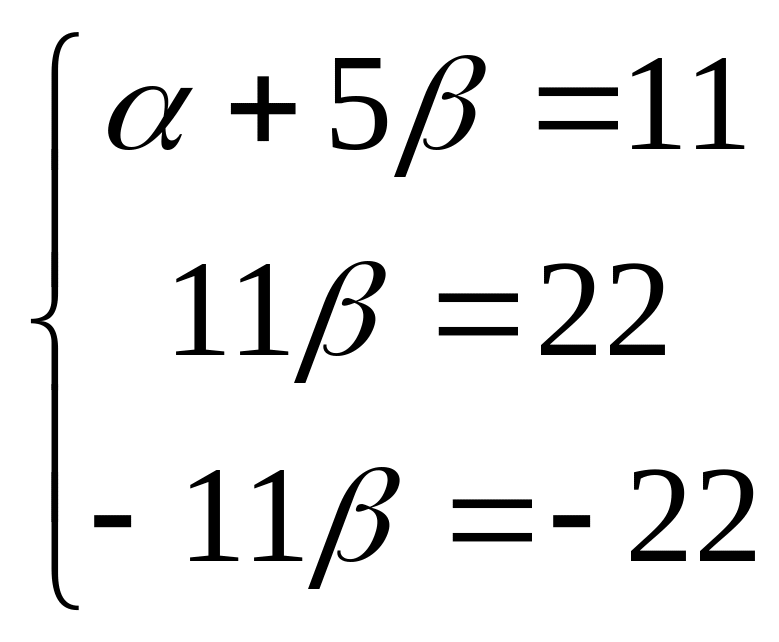отсюда видно, что , тогда .

Ответ. коэффициенты линейной комбинации равны 1 и 2.

Задача 6. Найти ранг матрицы .

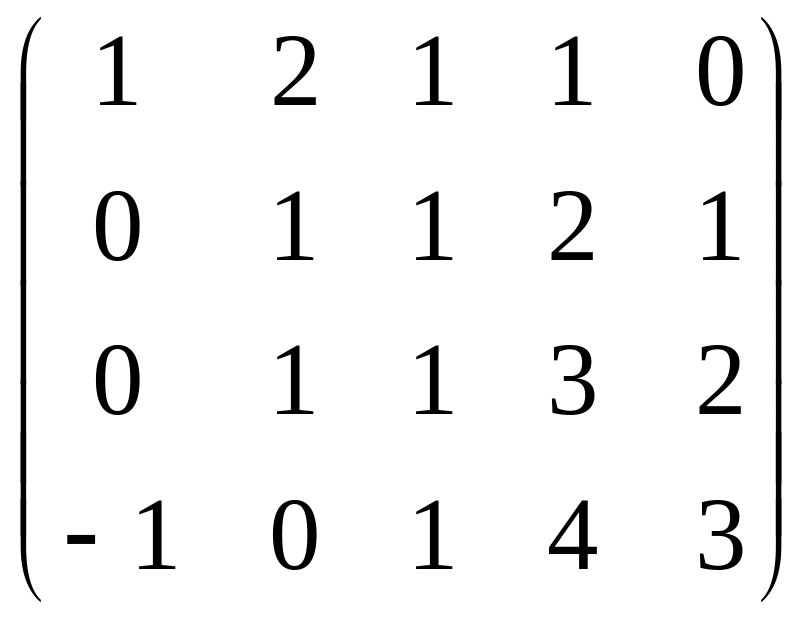Решение. Преобразуем методом Гаусса к треугольной форме.

.

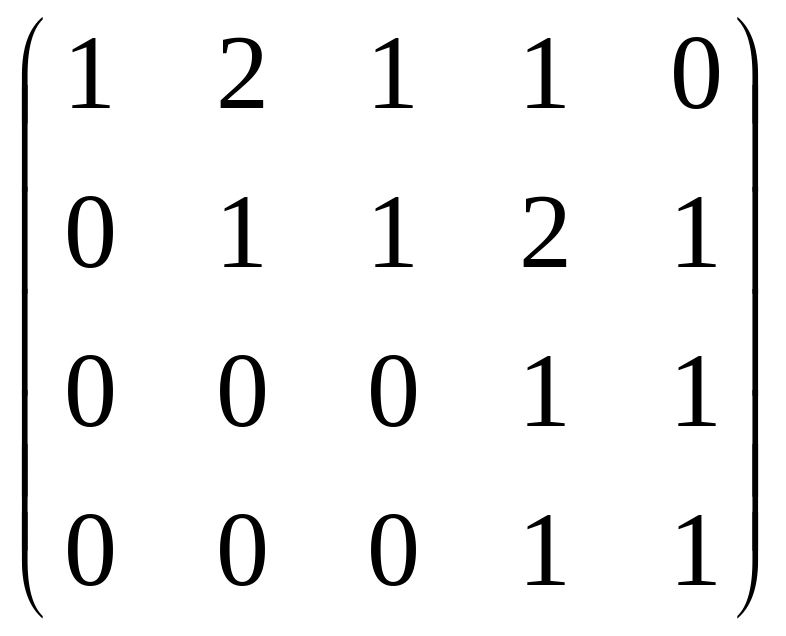
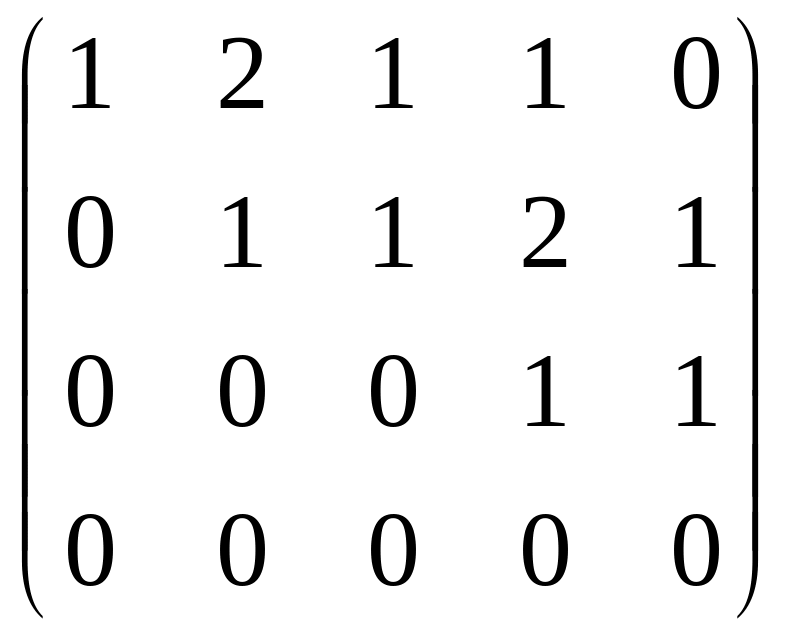Видно, что 4-я строка из нулей, поэтому ранг не равен 4, то есть . Минор порядка 2 легко находится в верхнем левом углу, но угловой минор порядка 3 равен 0. Однако это ещё не значит, что ранг равен 2, ведь можно отступить к правмому краю матрицы и взять минор с разрывом, из 1,2,4 столбцов, например такой:

Этот минор невырожденный, и он тоже является окаймляющим (ведь он полностью включает в себя квадрат, закрашенный жёлтым). Мы нашли базисный минор порядка 3. Также можно было рассматривать аналогичное в 1,2,5 столбцах, тоже минор порядка 3.

Ответ. .

Задача 7. Найти такие параметры , что ранг матрицы равен 1:

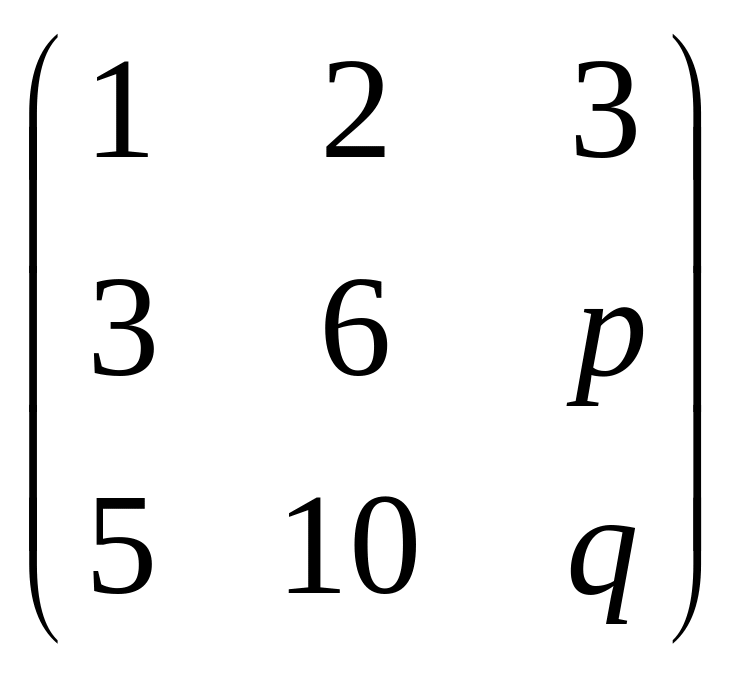
Решение. Преобразуем методом Гаусса к треугольной форме.

.

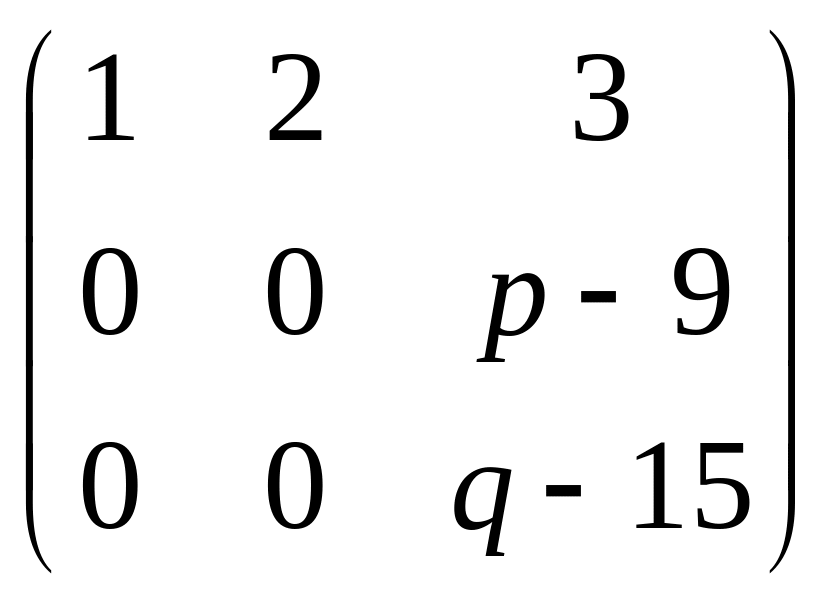Если и , то две последних строки только из нулей, и равен будет равен 1.

Ответ. , .

Задача 8. Найти ранг матрицы (4*4, можно с произвольными элементами, заданными группой).

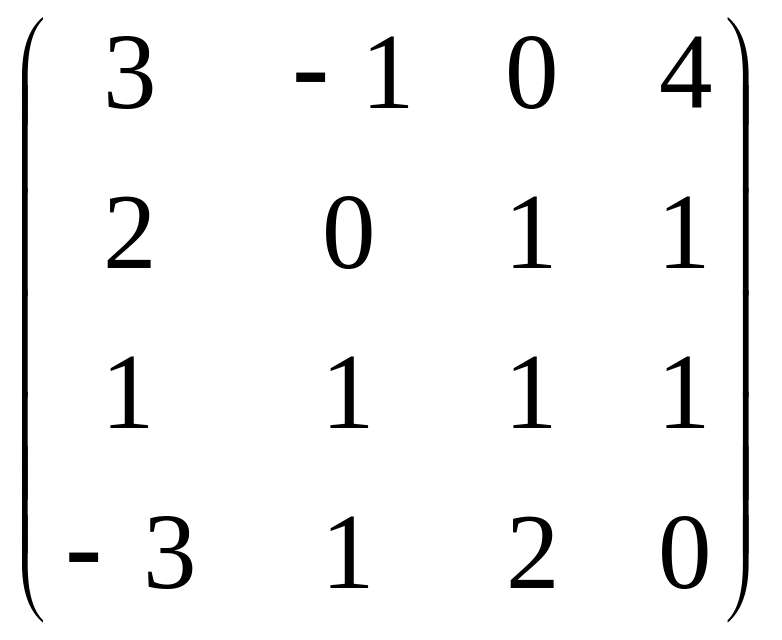
Решение. Для удобства преобразования методом Гаусса, сначала поменяем местами 1 и 3 строки. Ещё можно сразу прибавить 3-ю строку к 4-й.

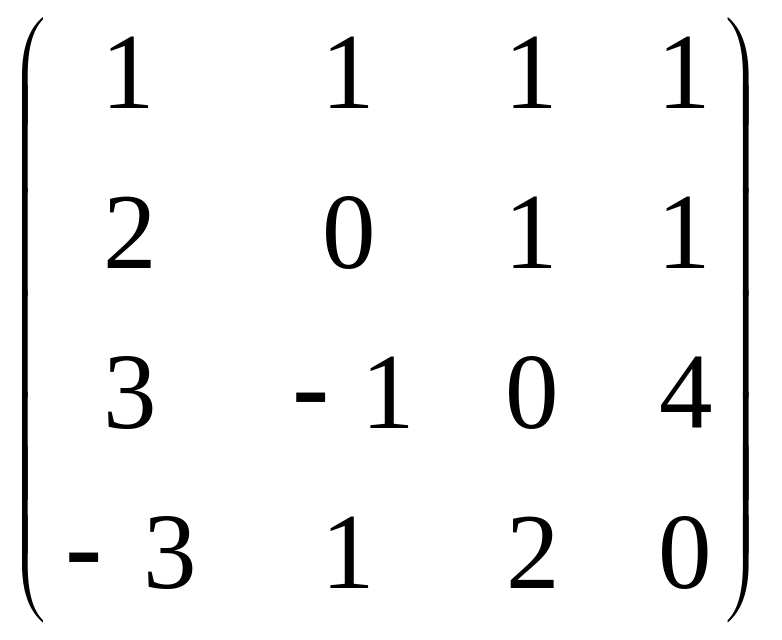
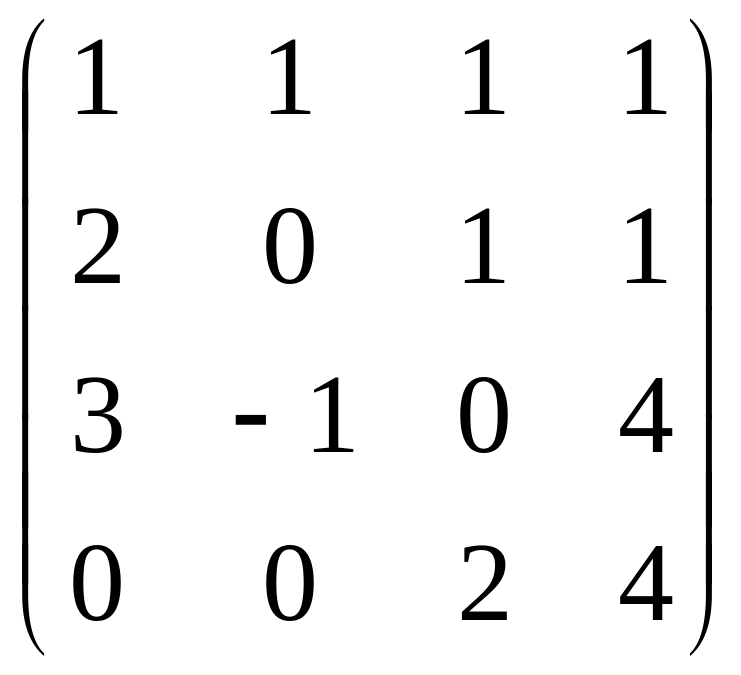
Дальше стандартным методом, обнулим всё ниже угла.

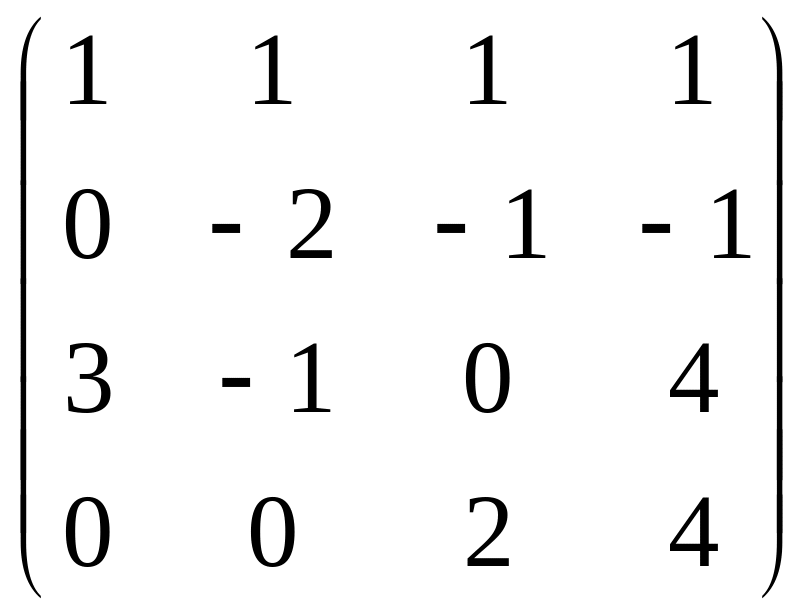
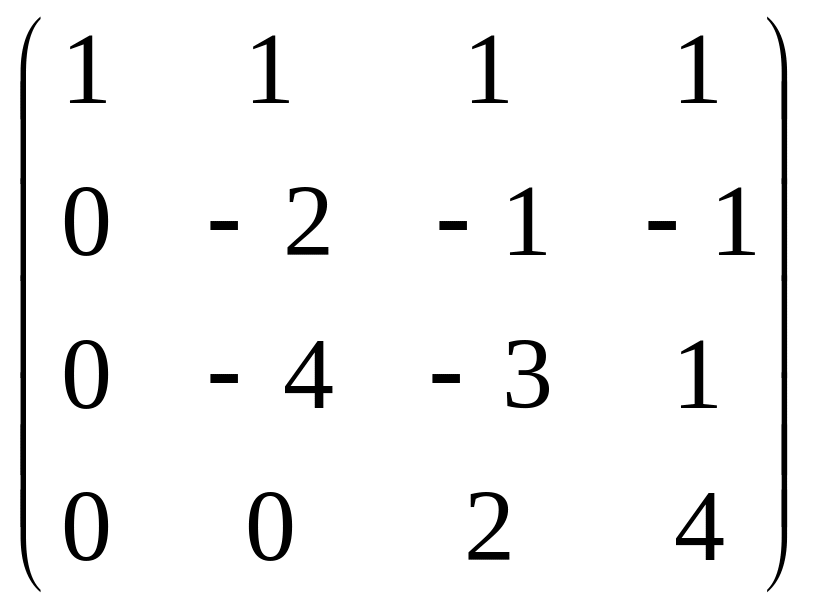
Для удобства вычислений домножим 2 строку на (-1), ранг при этом не меняется. Затем прибавим к 3 строке удвоенную 2-ю.

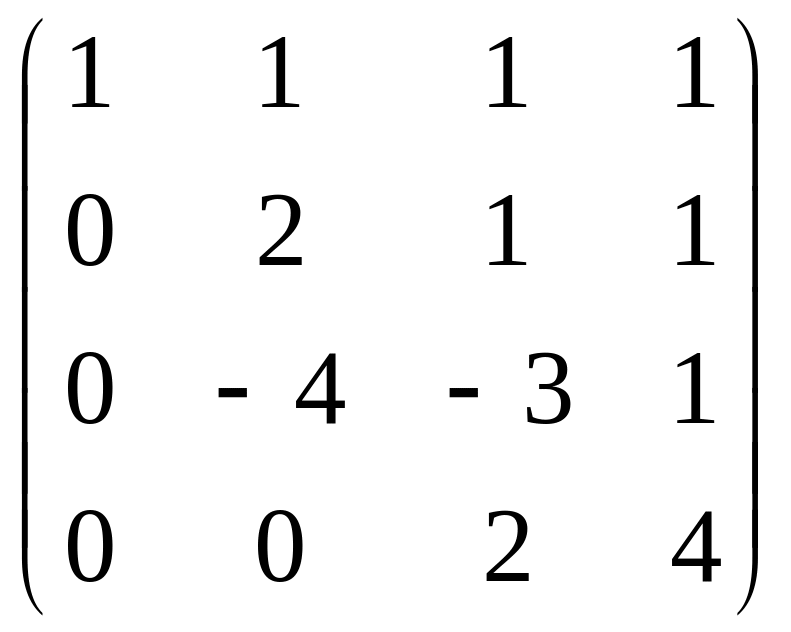
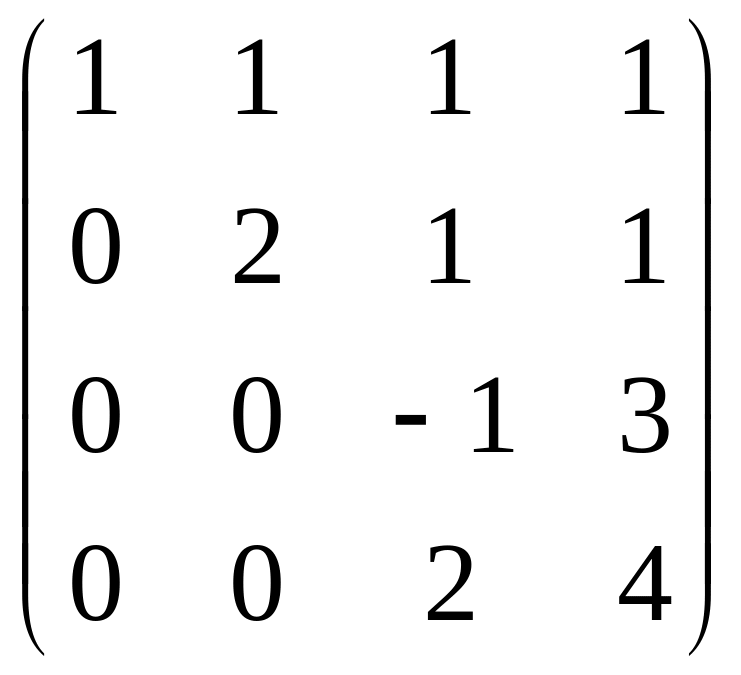
Теперь осталось прибавить к 4 строке удвоенную 3-ю.

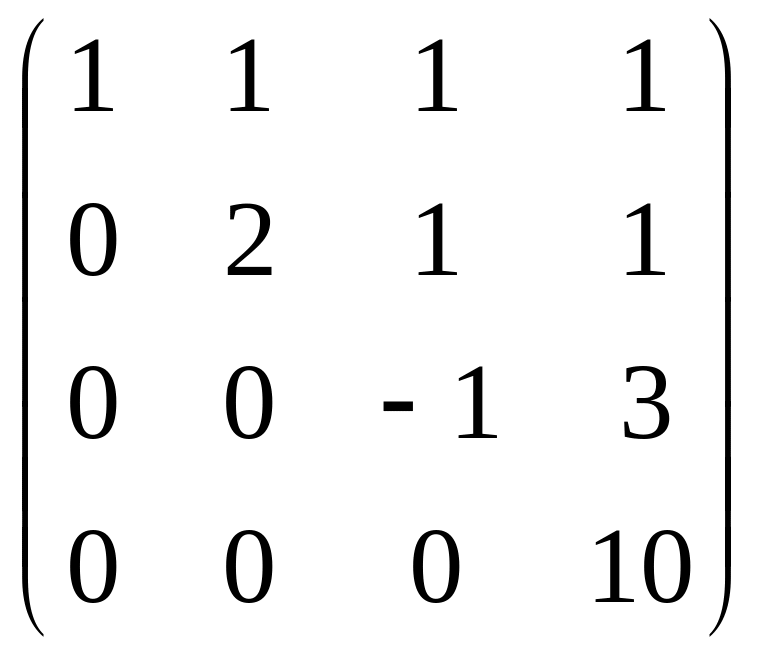. Видно, что получилась треугольная матрица, то есть определитель 4 порядка невырожденный. Поэтому .

Ответ. .

Элементы векторной алгебры.

Задача 9. (8.16 [1]) Найти косинус угла между векторами .

Решение. Известно, что .

, .

, тогда , что приблизительно равно 0,5, то есть угол чуть больше 60⁰.

Ответ. cos = 9/19.

Задача 10. Найти скалярное и векторное произведение векторов:

и .

Решение. .

Для поиска векторого произведения запишем определитель.

= = .

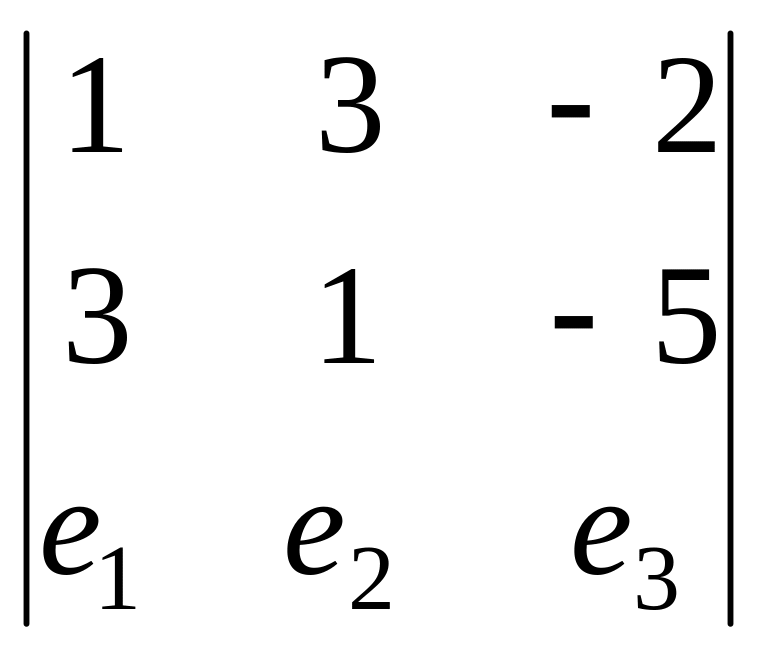Ответ. Скалярное: 16, векторное: (-13, -1, -8).

Задача 11. Дано: , , , , угол между векторами 45 градусов. Найти .

Решение. = = .

Примечание. Как видим, можно вычислять скалярное произведение, даже не зная коорднат векторов. Здесь фактически служат в качестве базисных векторов, и через них выражены , то есть (1,1) и (2,1) координаты относительно базиса .

Ответ. .

Практика № 6 (23 сентября у обеих групп).