Задание

В соответствии с вариантом (таблица 5) выполнить поиск оптимальных параметров динамического компенсатора колебаний методом покоординатного спуска.

Таблица 5 – Исходные данные

Первая цифра	m, кг	с, Н/мм	k; Н/мм	Вторая цифра	λ, кг/с	m1; кг	с1, Н/мм
0	10	10000	500	0	700	2	3000
1	13	17500	600	1	950	3,5	5000
2	8	11000	700	2	600	4	4000
3	15	20000	800	3	700	5	6000
4	17	15500	900	4	950	6	7000
5	12	14000	500	5	750	5,5	4500
6	6	9000	300	6	650	4,5	3500
7	20	16000	400	7	900	3	5500
8	22	12000	550	8	800	2,5	6500
9	16	13000	650	9	600	7	7000

Для всех вариантов приняты глубина резания 1 мм и коэффициент вязкого трения динамического компенсатора колебаний, равный коэффициенту вязкого трения основной системы.

Содержание протокола

В протоколе представить динамическую модель системы, исходные данные, график переходной характеристики системы без динамического компенсатора колебаний, рассчитать её параметр динамического качества, таблицу поиска экстремума с иллюстрирующим графиком и график переходной характеристики системы с оптимальными параметрами динамического компенсатора колебаний. Вывод.

4. Частотные характеристики технологической системы при резании

Частотные характеристики используются для оценки динамических свойств металлорежущих станков, их отдельных узлов, процессов резания и других управляемых объектов. По частотным характеристикам можно судить о качестве и возможной производительности процесса резания в замкнутой технологической системе, поскольку в большинстве случаев шероховатость обработанной поверхности и предельная глубина резания ограничиваются виброустойчивостью технологической обрабатывающей системы.

Для динамических испытаний узлов металлорежущих станков (МРС) применяют специальные установки, которые состоят из звукового генератора (ЗГ), усилителя мощности (УМ), электромагнитного вибратора (ЭМВ), источника постоянного тока (ИПТ), измерителя вектора механических усилий (ИМУ), измерителя вектора виброперемещений (ИВВ) и двухкоординатного стола (ДС) (рисунок 13).

Электромагнитный вибратор мод. ЛДС-62 выполнен бесконтактным, что позволяет определять частотные характеристики непосредственно на шпинделе станка, когда он вращается (рисунок 14).

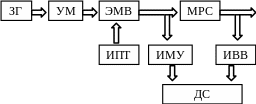
Рис. 13 – Схема экспериментальной установки

Рис. 14 – Конструкция электромагнитного вибратора

Вибратор состоит из корпуса 1, в котором установлен сердечник 2 из Ш-образного трансформаторного железа с обмотками 3, 4 и 5, а также вибродатчик 6 (модели ЛДС-29-70). При экспериментальном определении частотных характеристик, например, вращающегося шпинделя токарного станка, корпус вибратора устанавливают в резцедержатель 7 станка, а в шпиндель 8 – оправку 9. Конструкция вибратора позволяет изменять угол действия вектора возмущающих усилий за счёт винта 10 в пазу 11.

При работе виброустановки на обмотку 3 от генератора (ЗГ) через усилитель мощности (УМ) подаётся напряжение U = U_м sin ωt и постоянное напряжение U₀ от (ИПС) на обмотку 4. В результате в системе возбуждается силовое возмущение Р = Р_м sin ωt + Р₀. Это возмущение измеряется с помощью измерительной обмотки 5, а колебания (виброперемещения) упругой системы станка S = S_м sin(ωτ + φ) + S₀ измеряются измерительным прибором 6. В качестве измерителей векторов усилий и виброперемещений в установке использованы тензометрический усилитель, фазочувствительный вольтметр и автоматический регулятор фазы. Регистрация АФЧХ выполняется двухкоординатным столом модели ПДС-021Г.

АФЧХ можно построить и более простыми средствами по результатам сравнения осциллограмм изменения возмущения Р и виброперемещения S, записанных на шлейфовом осциллографе или самописце, который подключён к выходу тензометрического усилителя. Пример экспериментально полученной АФЧХ (частота в Гц) показан на рисунке 15.

I_m

Рис. 15 – АФЧХ станка мод. 16Б20А с гидростатическими

опорами шпинделя (масло И5А, давление 3 МПа)

При изучении частотных характеристик процесса резания в упругой технологической обрабатывающей системе различают характеристики первого и второго рода. Частотные характеристики первого рода получают экспериментально, задавая инструменту и детали относительные колебания в зоне резания, то есть при кинематическом возбуждении (рис. 16, а). Входным воздействием является виброперемещение x(t) инструмента (или инструментального суппорта) под влиянием вибратора 1, а выходной величиной – сила резания P(t) или её составляющая, измеряемая с помощью трёхкомпонентного динамометра 2. Эксперимент проводят при точении детали 3, имеющей равномерный припуск.

Динамические частотные характеристики второго рода получают при обработке специально подготовленной детали 3 с припуском x(t), который изменяется по гармоническому или близкому к нему закону (рисунок 16, б).

а б

Рис. 16 – Схемы определения частотных характеристик

процесса резания:

а – первого рода; б – второго рода

Рекомендуется проводить определение частотных характеристик первого и второго рода за два прохода обработки детали на специальной автоматизированной установке. На первом проходе происходит срезание равномерного припуска при включённом вибраторе, а на втором – срезание следа при отключённом вибраторе. Экспериментальная установка непосредственно связана с ЭВМ, которая выполняет обработку экспериментальных данных.

Экспериментальные частотные характеристики упругой технологической системы при резании, которые связывают изменения припуска с изменением упругих деформаций системы и характеризуют технологическую наследственность, можно получить в производственных условиях без применения сложной и весьма дорогостоящей аппаратуры.

Предлагается следующая схема эксперимента. При постоянных установках инструмента обрабатывают на разных частотах вращения шпинделя в исследуемом диапазоне специально подготовленную деталь с припуском, который гармонически изменяется. Измеряя с помощью кругломера или непосредственно на станке с помощью индикатора отклонения обработанной поверхности и записывая угол, можно построить график зависимости максимальной деформации системы и соответствующего фазового угла в функции частоты. Сравнивая полученные зависимости с расположением припуска, находят частотные характеристики. Проще всего подготовить деталь с припуском, который изменяется эксцентрично, хотя при этом характер изменения припуска отличается от гармонического, а эксперимент можно провести только в низкой области частот, ограниченной возможностями повода главного движения станка. Кроме того, вследствие плавного характера изменения припуска и наследственного следа на обработанной поверхности детали возникают трудности с определением ФЧХ. Однако, учитывая, что эксцентричное расположение припуска наиболее часто встречается на практике, из этого эксперимента можно получить ценную информацию для прогнозирования технологической наследственности.

Таким образом, эксперименты для определения частотных характеристик являются довольно трудоёмкими и требуют некоторого специального оснащения. На этапе технологической подготовки производства целесообразно провести моделирование этого эксперимента с помощью прикладной программы, интерфейс которой представлен на рисунке 17, что значительно сократит затраты.

Программа предназначена для моделирования экспериментального исследования частотных свойств технологической системы при точении. Динамическая модель технологической системы, в зависимости от степени идеализации, может быть представлена одномассовой, двухмассовой или трёхмассовой системой. В случае выбора одномассовой системы в модель входит упругая система, которая сведена к резцедержателю и процесс точения, происходящий в замкнутой технологической системы. В случае выбора двухмассовой системы динамическая модель состоит из резцедержателя и суппорта, а при трёхмассовой системе к ним добавляется динамическая модель шпинделя. При любом выборе в математическую модель входит процесс резания, представленный с учётом замкнутости технологической системы.

При моделировании исследуется процесс обработки специально подготовленной детали, контур которой в поперечном сечении сформирован по гармоническому закону. Таким образом, на упругую технологической системы действует возмущение в виде припуска Н_з (линия 2 на рисунке 17), который изменяется также по гармоническому закону. Амплитуда гармонического закона постоянна, а частота изменяется исследователем во время эксперимента.

Реакция упругой технологической системы наблюдается на осциллографе как изменение составляющей P_y силы резания (линия 1) и упругой деформации в направлении оси Y (линия 3). Зависимость амплитуды, которая измеряется как отношение максимальной величины упругой деформации к максимальной величине глубины резания и фазы, которая равняется углу между пиками упругой деформации и глубины резания, от частоты определяет амплитудно-фазовую частотную характеристику второго рода данной технологической системы.

При нажатии на кнопки «Запомнить точку АФЧХ» в таблице появляются соответствующие данные. После изменения частоты при нажатии на кнопку «Запомнить точку АФЧХ» данные будут автоматически записаны в следующую строчку таблицы.

При наличии данных, которые определяют не менее чем три точки, нажатие на кнопку «Построить АФЧХ» приводит к появлению дополнительного интерфейса с соответствующим графиком. Надписи возле экспериментальных точек отвечают значению частоты, а кривая графика построена как Эрмитов кубический сплайн, проходящий через все точки.

Результаты исследований в виде амплитудно-фазовой частотной характеристики (рисунок 18) получены при имитационном моделировании технологической системы с помощью прикладной программы.

Рис. 17 – Главный интерфейс прикладной программы

На характеристике отчётливо наблюдаются три петли, что вполне соответствует представлению модели технологической системы в виде трёхмассовой динамической системы. Первая петля (диапазон частот от 300 до 1500 рад/с) характеризует первую резонансную частоту, отражающую влияние резцедержателя, вторая (диапазон частот от 600 до 800 рад/с) и третья (диапазон частот от 800 до 1300 рад/с) отражают влияние динамических систем суппорта и шпинделя соответственно. Сравнение с экспериментальной АФЧХ свидетельствует о качественной адекватности математической модели и прикладной программы.

Рис. 18 – АФЧХ моделируемой системы при трёхмассовой модели

Параметры динамической модели и процесса резания ТОС соответствуют указанным на интерфейсе программы (рисунок 17).

Амплитудно-частотная характеристика показывает искажение амплитуды входной гармоники переменной составляющей припуска, а фазово-частотная характеристика – фазовый угол сдвига этой гармоники к соответствующей исходной гармонике.