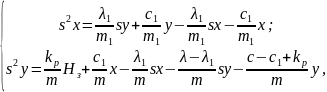2.1.3. Содержание протокола
В протоколе представить исходные данные (в соответствии с вариантом); копию интерфейса для любого значения варьируемого параметра; таблицу экспериментальных данных; графики соответствующих зависимостей. Анализ, выводы.
3. Экспериментальные исследования переходных процессов при точении
Исследования переходных процессов, происходящих в технологической системы при резании, позволяют определить основные динамические характеристики во временном диапазоне, наметить пути к улучшению динамического качества системы. Поскольку любая математическая модель является некоторой идеализацией реальной системы, наиболее достоверные результаты могут быть получены только экспериментальным путём. Проведение экспериментов по определению переходных характеристик технически значительно проще, чем экспериментальных исследований в частотном диапазоне и поэтому начинать работу по исследованию динамических явлений следует с проведения именно таких экспериментов. При выполнении экспериментов создание ступенчатого воздействия на систему проще всего обеспечить за счёт резкого увеличения или уменьшения глубины резания. В связи с высокими динамическими свойствами упругой технологической системы (ТС) и процесса резания на реальном оборудовании, для получения адекватных переходных характеристик скорость изменения входного воздействия должна быть очень высокой. В противном случае такое влияние нельзя считать ступенчатым, а реакцию системы – переходной характеристикой. Поэтому иногда легче получить весовые характеристики, которые представляют собой реакцию системы на импульсное воздействие и содержат в себе необходимые данные для идентификации.
Для проведения экспериментальных исследований динамических характеристик зависимости силы резания от глубины или толщины срезаемого слоя, при точении станок должен быть оснащён специальной установкой (рисунок 9), состоящей из трёхкомпонентного тензометрического динамометра (ТД), подключённого к тензометрическому усилителю (ТУ) и регистрирующему устройству (РУ). В качестве регистрирующего устройства может быть использован ПК с аналого-цифровым преобразователем и соответствующим программным обеспечением.
а б
Рис. 9 – Схема экспериментальной установки (а)
и сечение заготовки (б)
3.1. Улучшение динамических характеристик тос
Улучшение динамических характеристик производится с помощью динамического гасителя колебаний, который представляет собой дополнительную массу, присоединяемую к основной системе через упругую связь и элемент трения.
Примером конструкции динамического компенсатора колебаний с вязким трением может быть масса, которая подвешена на упругих элементах и входит с небольшим зазором в корпус, заполненный вязкой жидкостью. Специальные оправки, которые компенсируют колебания, для расточного инструмента рассеивают энергию колебаний за счёт сопротивления резины или полимера, заполняющих промежуток между двумя частями оправки.
Практика подтвердила эффективность применения в борштангах динамических компенсаторов колебаний с упруго деформируемыми элементами из высоко полимерных материалов (рисунок 10, а).
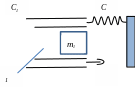
Рис. 10 – Компенсатор колебаний и его динамическая модель
Масса компенсатора 1 располагается на одной оси с борштангой 2, а в качестве упругих элементов используются кольца 3 из микропористой резины. Компенсатор такого типа устраняет изгибные колебания консольного инструмента в широком диапазоне частот и режимов резания. Экспериментальные исследования показали, что предельная глубина резания при работе с таким компенсатором увеличивается более чем в 2 раза.
В инженерной практике задачи расчёта динамического компенсатора колебаний чаще всего сводятся к выбору оптимальных массы и жёсткости компенсатора при заданном коэффициенте вязкого трения, которое определяется свойствами используемого демпфирующего материала. Динамический компенсатор колебаний вместе с упругой технологической системой станка представляет собой двухмассовую динамическую систему (рисунок 10, б), математическая модель которой, с учётом замкнутости ТОС, может быть представлена в виде:
|
(12) |
где Нз и Нф – заданная и фактическая глубина резания;
y, x – упругие деформации основной и дополнительной масс;
P – радиальная составляющая силы резания;
kp – коэффициент линеаризованной зависимости силы резания от глубины;
т, т1 – массы;
с, c1 – жёсткости;
λ, λ1 – коэффициенты вязкого трения основной системы и компенсатора соответственно.
Преобразуем систему (12) в два уравнения, решённых относительно старших производных:
|
(13) |
Добавление дополнительной массы с упругой связью и трением изменяет динамические свойства всей системы в целом. Причём изменения могут быть как в сторону улучшения, так и ухудшения динамических свойств. Поэтому, для получения желаемого эффекта гашения колебаний необходимо выбрать такие оптимальные параметры присоединяемой системы, которые, безусловно, приведут к успеху.
По уравнениям системы (13) можно проводить моделирование с целью определения оптимальных значений параметров динамического гасителя колебаний, а в качестве критерия оптимальности можно принять показатель динамического качества, который рассчитывается по зависимости (10).
Несмотря на очевидный эффект компенсации колебаний, который оценивается непосредственно по переходной характеристике, нередко требуется провести дополнительные исследования с использованием частотных характеристик системы.