
ГБОУ АО СПО «Астраханский колледж вычислительной техники»
Специальность 230113 230115 220703 140448 090305
ПРАКТИЧЕСКАЯ РАБОТА № 3 Применение уравнений и построение графиков материальной точки, совершающей механические колебания, для решения задач по дисциплине: «Физика»
Составил преподаватель: Аксёнова Л.А.
Рассмотрено на заседании цикловой комиссии математических и общих естественно-научных дисциплин Протокол № от « » 2014 г. Рекомендовано для студентов
Председатель комиссии: Беляева М.В.
2014 |

Содержание
1 Цель работы 2
2 Порядок выполнения работы 2
3 Содержание отчета 27
4 Контрольные вопросы 27
5 Литература 27
Приложение А. Теоретические положения 28
Приложение Б. Примеры решения задач 30
Приложение В. 32
1 Цель работы
1.1. Для системы совершающей гармонические колебания:
а) уметь производить расчеты физической величины в определенный момент времени и определенной точке пространства;
б) по заданным параметрам уметь составить уравнение x(t); Vx(t); ax(t);
в) уметь строить графики зависимости Екx(t), Еnx(t) x(t); Vx(t); ax(t) собственных незатухающих колебаний материальной точки по известным параметрам;
г) уметь определять физические величины по графикам зависимости x(t); Vx(t); ax(t).
2 Порядок выполнения работы
2.1 Задание 1. Полученный ответ сравнить с предложенными («один из нескольких»).
Вариант 1 |
|
1 |
|
|
|
2. V увеличивается; a уменьшается |
|
3. V уменьшается; a увеличивается |
|
4. V увеличивается; a увеличивается |
|
|
5. V уменьшается; a уменьшается |
1. 0,09 с 2. 56,52 с 3. 1,884 с 4. 6,28 с 5. 3,14 с |
|
|
|
|
|
1. 4 м 2. 1 м 3. 0,25 м 4. 2П м 5. 0,5П м |
|
|
|
1. 8 рад 2. 0,28 рад 3. 0,28П рад 4. П/3 рад |
|
5. (0,28Пt + П/3) рад |
|
|
|
1. x=80cos(Пt + 0,5) 2. x=80cos 4Пt 3. x=0,8cosПt |
|
4. x=0,8cos 4Пt 5. x=0,8cos 2Пt |
|
|
|
|
|
1. 1,74 м/с2 2. 3,0 м/с2 3. 0,36 м/с2 |
|
4. 1,48 м/с2 5. 2,96 м/с2 |
|
|
|
|
|
1 |
|
2. 2π с |
|
3. 0,1π с |
|
4. 5π с |
|
|
5. 0,4π с |
1.
|
|
4.
|
|
|
|
1. амплитуду колебаний |
|
2. отклонение точки от положения равновесия в начальный момент времени |
|
3. период и частоту колебаний |
|
4. максимальную скорость прохождения точкой положения равновесия |
|
5. полный запас механической энергии
Вариант 2 |
|
1 |
1. Еn увеличивается Еk уменьшается |
2. Еn не изменяется Еk увеличивается |
|
3. Еn уменьшается Еk увеличивается |
|
4. Еn уменьшается Еk не изменяется |
|
5. Еn увеличивается Еk увеличивается |
|
2. Длина математического маятника 39,2 см. Найти частоту его колебаний. |
1. 4 гц 2. 2 гц 3. 4П гц 4. 10/4П гц 5. 2П гц |
|
|
3. Найти длину волны, если скорость волны 0,5 м/с, период колебаний 0,3 с. |
1. 0,15 м 2. 1,66 м 3. 0,8 м 4. 0,5П м 5. 0,3П м |
|
|
4. Уравнение гармонических колебаний имеет вид: x = 0,2cos(5Пt+П/3) Найти период колебаний; А; V0; a0. |
1. 0,2 с 2. 5П с 3. 0,4 с 4. П/3 с 5. 2,5 с |
|
|
5. Напишите уравнение гармонических колебаний, если амплитуда равна 7 см и за 2 мин. Совершается 240 колебаний. Начальная фаза П/2 рад. |
1. x=7cos(2Пt + П/2) 2. x=0,07cos(2Пt + П/2) |
3. x=0,07cos(Пt + П/2) 4. x=0,07cosПt |
|
5. x=0,07cos(4Пt + П/2) |
|
6. Груз подвешен на пружине в положении равновесия, деформация пружины составляет х = 2,5 см. Если груз сместить из положения равновесия, он начинает совершать колебания с периодом |
1. 0,3с 2. 0,4с 3. 0,5с 4. 0,6с 5. 0,7с |
|
|
|
|
7.
Если материальная точка массой 10 г
совершает гармонические колебания
по закону
|
1. 0,050 Н 2. 0,025 Н 3. 0,004 Н |
4. 0,040 Н 5. 0,064 Н |
|
|
|
8.
Для того чтобы период колебаний
математического маятника, находящегося
в кабине лифта, уменьшился в
|
1. вниз с ускорением 4,9 м/с2 |
2. вверх с ускорением 4,9 м/с2 |
|
3. вверх с ускорением 9,8 м/с2 |
|
4. вверх с ускорением 2,45 м/с2 |
|
5. вниз с ускорением 2,45 м/с2 |
|
9. Если амплитуда гармонических колебаний материальной точки равна 1 м, то путь, пройденный точкой за время Т, равное периоду гармонических колебаний, равен |
1. 1 м 2. 2 м 3. 4 м 4. 8 м 5. 2π м |
|
|
|
|
|
|
|
|

Вариант
3
1
2.
Еn
уменьшается Еk
увеличивается
3.
Еn
= const
Еk
увеличивается
4.
Еn
уменьшается Еk
= const
5.
Еn
уменьшается Еk
уменьшается
1.400
гц 2.20 гц 3.10/П гц 4.1/400 гц 5.400П
гц
1.0,003
с
2.333
с
3.0,3П
с
4.0,3/П
с
5.2П
с
1.1
гц 2. П гц 3.0,8 гц 4.0,5 гц 5.0,8П гц
1.
x=8cos2Пt
+ 3/2
П
2.
x=0,08cos2Пt
+ 3/2
П
3.
x=0,08cos(2П/60
t
+ 3/2
П)
4.
x=8cos(2Пt
+ 3/2
П)
5.
x=0,08cos(2Пt
+ 3/2
П)
 .
Как изменяются потенциальная и
кинетическая энергия маятника при
движении его из положения С в положение
Д?
.
Как изменяются потенциальная и
кинетическая энергия маятника при
движении его из положения С в положение
Д?
6. Если амплитуду колебаний математического маятника увеличить вдвое и период его колебаний увеличить вдвое, то полный запас механической энергии |
1. увеличится в 16 раз |
2. увеличится в 8 раз |
|
3. увеличится в 4 раза |
|
4. увеличится в 2 раза |
|
5. не изменится |
|
7. Если на некоторой планете период колебаний секундного Земного математического маятника окажется равным 2с, то ускорение свободного падения на этой планете равно (принять, что ускорение свободного падения на Земле 9,8 м/с2) |
1. 4,9 м/с2 |
2. 2,45 м/с2 |
|
3. 19,6 м/с2 |
|
4. 14,7 м/с2 |
|
5. 39,2 м/с2 |
|
8. Амплитуда колебаний пружинного маятника 4см, масса груза 400г, жесткость пружины 40 Н/м. Максимальная скорость колеблющегося груза равна |
1. 4 м/с |
2. 16 м/с |
|
3. 0,4 м/с |
|
4. 0,8 м/с |
|
5. 8 м/с |
|
9. Если массу груза 2кг, подвешенного на пружине и совершающего гармонические колебания с периодом Т, увеличить на 6кг, то период колебаний станет равным |
1.
|
2. 2Т |
|
3.
|
|
4.
|
|
5.
|

Вариант 4 |
|
1. Как изменяются скорость и ускорение маятника при его движении из положения А в положение В?
|
1. V уменьшается a увеличивается |
2. V уменьшается a уменьшается |
|
3. V увеличивается a уменьшается |
|
4. V увеличивается a увеличивается |
|
5. V увеличивается a =const |
|
2. Период колебаний математического маятника 1 с, найти его длину (g ≈ П2) |
1.1 м 2. П м 3.2П м 4. П/g м 5.0,25 м |
|
|
3. Длина волны 20 см, скорость волны 10 м/с. Найти частоту колебания. |
1.2 гц 2.0,5 гц 3.0,1 гц 4.200 гц 5.50 гц |
|
|
4. Уравнение гармонических колебаний имеет вид: x
= 5cos0,28Пt.
Найти начальную фазу; V0;
a0; |
1.5 рад 2.0 рад 3.0,28 рад 4.0,28П рад 5.2П рад |
|
|
5. Амплитуда колебаний равна 12 см, частота 50 гц. Найти смещение точки через 0,4 с. Начальная фаза колебании равна нулю. |
1.12 м 2.0,12 м 3.0 м 4.50 м 5.40П м |
|
|
6. Уравнение гармонических колебаний материальной точки, максимальная скорость которой 2π м/с, период колебаний 2с, смещение точки от положения равновесия в начальный момент 1м, имеет вид |
1.
|
2.
|
|
3.
|
|
4.
|
|
5.
|
|
7.
Ускорение материальной точки,
совершающей гармонические колебания
по закону
|
1. 2π2 м/с2 |
2. π2 м/с2 |
|
3. 0 м/с2 |
|
4. –π2 м/с2 |
|
5. –2π2 м/с2 |
|
8. Если амплитуду колебаний математического маятника увеличить вдвое и период его колебаний увеличить вдвое, то полный запас механической энергии |
1. увеличится в 16 раз |
2. увеличится в 8 раз |
|
3. увеличится в 4 раза |
|
4. увеличится в 2 раза |
|
5. не изменится |
|
9. Если массу груза 2кг, подвешенного на пружине и совершающего гармонические колебания с периодом Т, увеличить на 6кг, то период колебаний станет равным |
1. |
2. 2Т |
|
3. |
|
4. |
|
5. |
Вариант
5
1
2.
V
уменьшается a
уменьшается
3.
V
увеличивается a
уменьшается
4.
V
увеличивается a
увеличивается
5.
V
увеличивается a
=const
1.0,628
н/м 2. П н/м 3. П2
н/м 4.100 н/м 5.1 н/м
1.30
м/с 2.0,3 м/с 3.0,01 м/с 4. П м/с 5.0,03
м/с
1.96
рад 2.4П рад 3.4,5 рад 4.0,07 рад
5.32,5П рад
1.
x=0,06cos(П/3t
+
П/6)
2.
x=0,06cos(12Пt
+
П/6)
3.
x=6cos(12Пt
+
П/6)
4.
x=0,06cos12Пt
+
П/6
5.
x=0,06cos(6Пt
+
П/6)
1.
1,5 Н/м
2.
2,0 Н/м
3.
2,5 Н/м
4.
3 Н/м
5.
3,5 Н/м
1.
1.
0,3с
2.
0,4с
3.
0,5с
4.
0,6с
5.
0,7с
1.
2.
3.
4.
5.

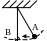 .
Как изменяются скорость и ускорение
маятника при его движении из положения
А в положение В?
.
Как изменяются скорость и ускорение
маятника при его движении из положения
А в положение В?
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]()
![]()
![]()
![]()
![]()
![]()

Вариант
6
1
.
Как изменяются потенциальная и
кинетическая энергия пружинного
маятника при его движении из положения
А в положение В?
1.
Еn
уменьшается Еk
увеличивается
2.
Еn
увеличивается Еk
уменьшается
3.
Еn
уменьшается
Еk
уменьшается
4.
Еn
увеличивается
Еk
увеличивается
5.
Еn
= const
Еk
= const
2
1.
Т увеличивается в 3 р
2.
Т уменьшается в 3 р
3.
Т не изменяется
4.
Т увеличивается в
5.
Т уменьшается в
р
3.
Какими параметрами отличаются две
волны?
2.
периодом
3.
частотой
4.
фазой
5.
амплитудой
1.1,5П
м
2.2П
м
3.0П
м
4.
-0,04П м
5.0,5П
м
1.x
= 0,05cos(2Пt
+ П/4)
2.
x = 5cos(2Пt
+ П/4)
3.
x = 0,05cos(2П 6,28t
+ П/4)
4.
x = 0,05cos2Пt
+ П/4
5.
x
= 0,05cos(2Пt
+
6,28)
 .
Амплитуду колебания математического
маятника увеличили в 3 раза. Как
изменится период колебания маятника?
.
Амплитуду колебания математического
маятника увеличили в 3 раза. Как
изменится период колебания маятника?
![]() р
р
6. К легкой пружине подвешиваются поочередно два разных груза. Период колебаний первого груза Т1 = 4с, второго Т2 = 3с. Если к пружине подвесить оба груза, то период колебаний будет равен |
1. 5с |
2. 6с |
|
3. 7с |
|
4. 8с |
|
5. 9с |
|
7. Амплитуда колебаний середины струны 1∙10-3м, частота колебаний 480 Гц. Максимальное значение скорости этой точки струны равно |
1. 1 м/с 2. 2 м/с 3. 3 м/с 4. 4 м/с 5. 5 м/с |
|
|
8. Чашка пружинных весов совершает малые колебания с периодом Т1 = 0,3с. Если на чашку весов опустить гирю массой m = 5 кг, период колебаний чашки с гирей станет равным T2 = 0,9с. Пружина невесома. Масса пустой чашки весов равна |
1. 425 г |
2. 575 г |
|
3. 625 г |
|
4. 725 г |
|
5. 875 г |
|
9.
Материальная точка равномерно вращается
по окружности радиуса R.
Время полного оборота Т = 6с. Через
какое время проекция этой точки на
ось, совпадающую с диаметром окружности,
сместится от центра окружности на
расстояние
|
1. 0,25с |
2. 0,5с |
|
3. 1с |
|
4. 2с |
|
5. 3с |

Вариант
7
1
.
Как изменяются потенциальная и
кинетическая энергия маятника при
его движении из положения А в положение
В?
2.
Еn
увеличивается Еk
увеличивается
3.
Еn
уменьшается Еk
уменьшается
4.
Еn
= const
Еk
увеличивается
5.
Еn
увеличивается Еk
уменьшается
1.
Т увеличиваетсяв 4 р
2.
Т уменьшается в 4 р
3.
Т увеличиваетсяв 2 р
4.
Т уменьшается в 2 р
5.
Т не изменяется
1.0,3
м
2.0,03
м
3.10
м
4.30
м
5.3
м
1.5/6
П м
2.2П
м
3.0,08
м
4.8П
м
5.2П/3
м
1.
x
= 0,01cos
2Пt
2.
x
= cos
2Пt
3.
x
= 0,01cos(2Пt
+ 2П)
4.
x
= cos(2Пt
+ 1)
5.
x
= 0,01cos(2Пt
+ П/2)
6.
Материальная точка равномерно движется
по окружности. В тот момент, когда
проекция этой точки на ось, совпадающую
с диаметром окружности, удалена на
расстояние х = 20см от центра окружности,
фаза колебаний проекции этой точки
на выбранную ось равна
|
1. 20см |
2. 24см |
|
3. 28см |
|
4. 92см |
|
5. 141см |
|
7. Материальная точка равномерно вращается по окружности радиуса R = 0,5м со скоростью V = 3 см/с. Определить период колебаний проекции этой точки на ось, совпадающую с диаметром окружности |
|
1. 16,7с 2. 52с 3. 81с 4. 105с 5. 120с |
|
|
|
|
|
8.
Движение тела вдоль оси х записывается
уравнением
|
1. 0,5с |
2. 0,8с |
|
3. 1с |
|
4. 3с |
|
5. 4с |
|
9.
Зависимость координаты х колеблющейся
материальной точки от времени имеет
вид
|
1. 1с |
2. 0,5с |
|
3. 0,1с |
|
4. 0,05с |
|
5. 0,01с |

Вариант
8
1
.
Как изменяются скорость и ускорение
маятника при его движении из положения
С в положение Д?
2.
V
уменьшается a
увеличивается
3.
V
увеличивается a
=const
4.
V
=const
a уменьшается
5.
V
увеличивается a
увеличивается
1.
Т не изменяется
2.
Т увеличиваетсяв 4 р
3.
Т уменьшается в 4 р
4.
Т увеличивается в 2 р
5.
Т уменьшается в 2 р
1.
амплитудой
2.
частотой
3.
фазой
4.
периодом
5.
циклической частотой
1.
8П рад
2.9,6
рад
3.8,25П
рад
4.11П/12
рад
5.
П/4 рад
1.
x
= 0,01cos
0,01Пt
2.
x
= cos
Пt
3.
x
= 0,01cos
20Пt
4.
x
= 0,01cos
40Пt
5.
x =
0,01
6. Один из математических маятников за некоторое время совершил 10 колебаний, а другой за это же время 6 колебаний. Разность длин маятников Δl = 0,16м. Длина маятника, совершившего 10 колебаний, равна |
1. 0,12м |
2. 0,11м |
|
3. 0,1м |
|
4. 0,09м |
|
5. 0,08м |
|
7. Груз массой 200г, прикрепленный к пружине, совершает гармонические колебания. Жесткость пружина 18 Н/м. За две минуты груз совершает количество колебаний, равное
|
1. 114 2. 156 3. 163 4. 181 5. 185 |
|
|
8.
Материальная точка равномерно вращается
по окружности. Зависимость ее проекции
на ось Ох, совпадающую с диаметром
окружности, от времени описывается
формулой
|
1. 0,2 м/с |
2. 0,6 м/с |
|
3. 3 м/с |
|
4. 6 м/с |
|
5. 30 м/с |
|
9.
Материальная точка равномерно
вращается по окружности. Зависимость
ее проекции на ось Ох, совпадающую с
диаметром окружности, от времени
описывается формулой
|
1. 2 м/с |
2. 3,5 м/с |
|
3. 4 м/с |
|
4. 8 м/с |
|
5. 8,5 м/с |

Вариант
9
1
.
Как изменяются кинетическая и
потенциальная энергия маятника при
его движении из положения А в положение
В?
2.
Еn
уменьшается Еk
увеличивается
3.
Еn
= const
Еk
= const
4.
Еn
увеличивается Еk
увеличивается
5.
Еn
уменьшается Еk
уменьшается
1.1
с
2.2П
с
3.0,628
с
4.100
с
5.10
с
1.50
м/с
2.0,1
м/с
3.500
м/с
4.50,1
м/с
5.5
м/с
1.3,5
гц
2.1,5
гц
3.0,04
гц
4.2/3
гц
5.3П
гц
1.
x
= 20cos
(2Пt+П/2)
2.
x
= 0,2cos
(4Пt+П/2)
3.
x
= 0,2cos
(4Пt+П/2)
4.
x
= 0,2cos
(2t+П/2)
5.
x
= 20cos
(4Пt+П/2)
1.
1.
12см 2. 15см
3.
18см
4.
22см
5.
25см
1.
36см 2. 53см
3.
89см
4.
120см
5.
180см
1.
0,16с
2.
0,21с
3.
0,26с
4.
0,32с
5.
0,37с
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]()
Вариант 10 |
|
1. Как изменяются скорость и ускорение маятника при его движении из положения А в положение В?
|
1. V увеличивается a уменьшается |
2. V уменьшается a увеличивается |
|
3. V увеличивается a увеличивается |
|
4. V уменьшается a уменьшается |
|
5. V увеличивается a =const |
|
2 |
1. уменьшился в 2 р |
2. увеличился в 2 р |
|
3.
уменьшился в
|
|
4. увеличился в р |
|
5. не изменился |
|
3
|
1. смещением |
2. амплитудой |
|
3. длиной волны |
|
4. скоростью |
|
5. фазой |
|
4. Уравнение гармонических колебаний имеет вид: x = cos(3П/2 t + П/4) Найти максимальное смещение от положения равновесия; V0; a0. |
1.0 м 2.3П/2 м 3. П/4 м 4.5/4 П м 5.1 м |
|
|
5. Напишите уравнение гармонических колебаний, если частота 1,2П-1 с, амплитуда 2 см, начальная фаза П/4 рад. |
1. x = 2cos(1,2П t + П/4) |
2. x = 0,02cos(1,2П t + П/4) |
|
3. x = 2cos(2,4Пt + П/4) |
|
4. x = 0,02cos 1,2Пt + П/4 |
|
5. x = 0,02cos(2П/1,2 t + П/4 |
|
6. Груз массой 100г совершает колебания на пружине жесткостью 250 Н/м. Если амплитуда колебаний 15см, то наибольшее значение модуля скорости тела равно |
1. 0,3 м/с |
2. 7,5 м/с |
|
3. 0,3 см/с |
|
4. 5 м/с |
|
5. 5 см/с |
|
7. Груз, подвешенный на пружине, в покое растягивает ее на 1см. Если сместить груз на 2 см вниз из нерастянутого положения и отпустить, то он начинает совершать гармонические колебания с периодом, равным |
1. 2,0с |
2. 0,3с |
|
3. 0,2с |
|
4. 0,4с |
|
5. 1,8с |
|
8. Материальная точка равномерно вращается по окружности радиусом R = 0,4 м, делая 5 оборотов в секунду. Определите скорость проекции этой точки на ось, совпадающую с диаметром окружности в тот момент, когда она, т.е. проекция, окажется на расстоянии от центра окружности |
1. 10,9 м/с |
2. 12,6 м/с |
|
3. 13,2 м/с |
|
4. 14,8 м/с |
|
5. 17,3 м/с |
|
9. Тело совершает гармонические синусоидальные колебания с периодом Т = 1,2с и нулевой начальной фазой. Через сколько времени после начала колебаний смещение тела от положения равновесия станет равным половине амплитуды? |
1. 0,1с |
2. 0,6с |
|
3. 0,4с |
|
4. 0,2с |
|
5. 0,3с |


2.2 Задание 2: решить задачи по вариантам и получить единственно правильный ответ.
В ариант
1
ариант
1
1. На какое расстояние S надо оттянуть груз массой m = 300г от положения равновесия, чтобы он, будучи прикреплен к пружине жесткостью к=0,2 кН/м, проходил через положение равновесия со скоростью V max = 10 м/с.
2.
Математический маятник колеблется с
частотой
![]() . Амплитуда его колебаний А = 5см. Чему
равна скорость маятника в тот момент,
когда его потенциальная энергия станет
равной кинетической. Начальная фаза
равна нулю.
. Амплитуда его колебаний А = 5см. Чему
равна скорость маятника в тот момент,
когда его потенциальная энергия станет
равной кинетической. Начальная фаза
равна нулю.
3. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени вмещение равно 4 см, а скорость – 10 м/с. Определить амплитуду и начальную фазу колебаний, если их период 2 с.
4. Найти: 1) вид колебаний; 2) уравнения x(t), Vx(t), ax(t); 3) положение, в котором Vmax, amax; 4) построить графики x(t), Vx(t); 5) ЕК, ЕП в т. А, В, С; 6) полную механическую энергию в т. А, В, С.
Вариант 2
1 .
Полная энергия тела, совершающего
гармонические колебания w
= 3∙10-5
Дж, максимальная сила, действующая на
тело Fmax
= 1,5∙10-3
Н. Написать уравнение движения этого
тела, если период колебаний Т = 20с и
начальная фаза 600.
.
Полная энергия тела, совершающего
гармонические колебания w
= 3∙10-5
Дж, максимальная сила, действующая на
тело Fmax
= 1,5∙10-3
Н. Написать уравнение движения этого
тела, если период колебаний Т = 20с и
начальная фаза 600.
2. Период колебания первого математического маятника Т1 = 3с, а второго Т2 = 4с. Чему равен период колебаний маятника, длина которого равна сумме длин первого и второго маятников?
3. Шарик массой 60 г колеблется с периодом 2 с. В начальный момент времени смещение шарика 4 см и он обладает энергией 0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон изменения возвращающей силы с течением времени.
4. Найти: 1) вид колебаний; 2) по графику Vx max, ω, υ; 3) amax, A(xmax); 4) уравнения x(t), ax(t); 5) Fmax; 6) Еполную.
Вариант 3
1 .
Упругая пружина под действием подвешенного
к ней груза, растянулась на 1 см. Если
груз еще немного оттянуть вниз и
отпустить, то она станет совершать
вертикальные колебания. Определить
период этих колебаний.
.
Упругая пружина под действием подвешенного
к ней груза, растянулась на 1 см. Если
груз еще немного оттянуть вниз и
отпустить, то она станет совершать
вертикальные колебания. Определить
период этих колебаний.
2. Чему равно отношение потенциальной энергии точки, совершающей гармонические колебания, к ее кинетической энергии для момента времени t = Т/6. Начальная фаза колебаний равна нулю.
3.
Полная энергия Е гармонически колеблющейся
точки равна 10 мкДж, а максимальная сила
Fmax,
действующая на точку, равна –0,5 мН.
Напишите уравнение движения этой точки,
если период Т колебаний равен 4 с, а
начальная фаза
![]() .
.
4. Найти: 1) вид колебаний математического маятника; 2) период собственных затухающих колебаний (Т); 3) частоту собственных незатухающих колебаний (ω0); 4) частоту собственных затухающих колебаний (ω); 5) коэффициент затухания β; 6) как Δ Еполная, А.
Вариант 4
1 .
Во сколько раз изменится частота
гармонических колебаний математического
маятника, если длину его нити уменьшить
на 30%.
.
Во сколько раз изменится частота
гармонических колебаний математического
маятника, если длину его нити уменьшить
на 30%.
2. Гиря, подвешенная к пружине, колеблется по вертикали с амплитудой А = 4см. Определить полную энергию колебаний гири, если под действием силы F = 10Н пружина удлинилась на х = 0,5м.
3. Определите отношение кинетической энергии Т точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания.
4.
Найти: 1) как Δ Vх,
Δ
aх;
2) как Δ ЕП,
ЕК;
3) Т, υ (m
= 1 кг,
![]() );
4) ω; 5) уравнения x(t),
Vx(t).
);
4) ω; 5) уравнения x(t),
Vx(t).
В ариант
5
ариант
5
1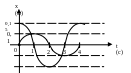 .
Когда груз, совершающий колебания на
вертикальной пружине имел массу m1,
период колебаний был равен Т1
= 4с, а когда его масса стала равной m2,
период стал равен Т2
= 5с. Каким будет период Т, если масса
груза будет равна сумме масс m1
+ m2?
Массы m1
и m2
неизвестны.
.
Когда груз, совершающий колебания на
вертикальной пружине имел массу m1,
период колебаний был равен Т1
= 4с, а когда его масса стала равной m2,
период стал равен Т2
= 5с. Каким будет период Т, если масса
груза будет равна сумме масс m1
+ m2?
Массы m1
и m2
неизвестны.
2.
Через какое время, считая от начала
колебаний смещение гармонически
колеблющейся точки составит
![]() амплитуды? Период колебаний точки T
= 2c.
амплитуды? Период колебаний точки T
= 2c.
3.
Материальная точка колеблется согласно
уравнению
![]() ,
где А = 5 см и
,
где А = 5 см и
![]() .
Когда возвращающая сила F
в первый раз достигает значения –12 мН,
потенциальная энергия П точки оказывается
равной 0,15 мДж. Определите: 1) этот момент
времени t;
2) соответствующую этому моменту фазу
.
Когда возвращающая сила F
в первый раз достигает значения –12 мН,
потенциальная энергия П точки оказывается
равной 0,15 мДж. Определите: 1) этот момент
времени t;
2) соответствующую этому моменту фазу
![]() .
.
4. Найти: 1) А1, А2; 2) Т1, Т2; 3) ω1, ω 2; 4) х1(t), х2(t); 5) Vmax, amax.
Вариант 6
1 .
Математический маятник массой m=0,01кг
колеблется согласно уровню
.
Математический маятник массой m=0,01кг
колеблется согласно уровню
![]() .
Найти максимальную силу, действующую
на него и его полную механическую
энергию. Чему равна длина маятника?
.
Найти максимальную силу, действующую
на него и его полную механическую
энергию. Чему равна длина маятника?
2. Во сколько раз изменится частота колебаний резиновой нити, если от нее отрезать четверть длины, а груз оставить тот же?
3. Если увеличить массу груза, подвешенного к спиральной пружине, на 600 г, то период колебаний груза возрастает в 2 раза. Определите массу первоначально подвешенного груза.
4. Найти: 1) вид колебаний; 2) уравнения x(t), Vx(t), ax(t); 3) положение, в котором Vmax, amax; 4) построить графики x(t), Vx(t); 5) ЕК, ЕП в т. А, В, С; 6) полную механическую энергию в т. А, В, С.
В ариант
7
ариант
7
1.
Амплитуда гармонического колебания
точки А = 5см, период Т = 4с. Найти максимальную
скорость точки, а также ее скорость
через
![]() от начала колебания. Найти максимальное
ускорение.
от начала колебания. Найти максимальное
ускорение.
2. К пружине подвешен груз. Зная, что максимальная кинетическая энергия колебаний груза wmax k = 1 Дж, найти жесткость пружины. Амплитуда колебаний 5 см.
3. Однородный диск радиусом R = 20 см колеблется около горизонтальной оси, проходящей на расстоянии l = 15 см от центра диска. Определите период Т колебаний диска относительно этой оси.
4. Найти: 1) вид колебаний; 2) по графику Vx max, ω, υ; 3) amax, A(xmax); 4) уравнения x(t), ax(t); 5) Fmax; 6) Еполную.
Вариант 8
1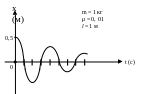 .
За одинаковое время один маятник
совершает N1
= 50 колебаний, а второй – N2
= 25 колебаний. Найти их длины l1
и l2
, если один из них короче второго на
.
За одинаковое время один маятник
совершает N1
= 50 колебаний, а второй – N2
= 25 колебаний. Найти их длины l1
и l2
, если один из них короче второго на
![]() =33см.
=33см.
2. Человек массой m = 80кг качается на качелях. Амплитуда его колебаний А=1 м. За t1 = 1 мин. он совершает N1 = 15 колебаний. Найти кинетическую и потенциальную энергию человека через t = Т / 6. Начальная фаза равна нулю.
3 .
Тонкий однородный стержень длиной l
= 60 см может свободно вращаться вокруг
горизонтальной оси, отстоящей на
расстоянии х = 15 см от его середины.
Определите период колебаний стержня,
если он совершает малые колебания.
.
Тонкий однородный стержень длиной l
= 60 см может свободно вращаться вокруг
горизонтальной оси, отстоящей на
расстоянии х = 15 см от его середины.
Определите период колебаний стержня,
если он совершает малые колебания.
4. Найти: 1) вид колебаний математического маятника; 2) период собственных затухающих колебаний (Т); 3) частоту собственных незатухающих колебаний (ω0); 4) частоту собственных затухающих колебаний (ω); 5) коэффициент затухания β; 6) как Δ Еполная, А.
Вариант 9
1. Материальная точка совершает гармонические колебания с амплитудой А = 10см и периодом Т = 2с. Написать уравнение этих колебаний и найти фазу колебаний, когда смещение точки стало равна 5см.
2. Легкая пружинка с жесткостью к = 0,2Н/см подвешена к штативу. В некоторый момент к ее свободному концу подвесили массой m = 100г и осторожно отпустили. Запишите уравнение колебаний груза x=x(t), приняв за начало отсчета колебаний и времени наложения равновесия пружины с грузом.
3. Два математических маятника, длины которых отличаются на Δl = 16 см, совершают за одно и то же время один n1 = 10 колебаний, другой – n2 = 6 колебаний. Определите длины маятников l1 и l2.
4. Найти: 1) как Δ Vх, Δ aх; 2) как Δ ЕП, ЕК; 3) Т, υ (m = 1 кг, ); 4) ω; 5) уравнения x(t), Vx(t);
В ариант
10
ариант
10
1. Если к шарику массой m1, колеблющемуся на пружине, подвесить снизу еще один шарик массой m2 = 300г, то частота колебаний уменьшается в 2 раза. Чему равна масса m1 первого шарика.
2. Амплитуда гармонических колебаний материальной точки А = 2см, полная энергия колебаний w = 3∙10 -7 Дж. При каком смещении х от положения равновесия на колеблющуюся точку действует сила F = 2,25∙10 -3 Н.
3.
Математический маятник, состоящий из
нити длиной l
= 1 м и свинцового шарика радиусом r
= 2 см, совершает гармонические колебания
с амплитудой А = 6 см. Определите: 1)
скорость шарика при прохождении им
положения равновесия; 2) максимальное
значение возвращающей силы. Плотность
свинца
![]() .
.
4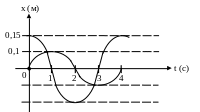 .
Найти: 1) А1,
А2;
2) Т1,
Т2;
3) ω1,
ω
2;
4) х1(t),
х2(t);
5) Vmax,
amax.
.
Найти: 1) А1,
А2;
2) Т1,
Т2;
3) ω1,
ω
2;
4) х1(t),
х2(t);
5) Vmax,
amax.

 .
Как изменяются скорость и ускорение
маятника при движении его из положения
А в положение В?
.
Как изменяются скорость и ускорение
маятника при движении его из положения
А в положение В?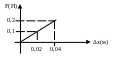 .
0,2π с
.
0,2π с
 .
Как изменяются потенциальная и
кинетическая энергия маятника при
его движении из положения С в положение
Д?
.
Как изменяются потенциальная и
кинетическая энергия маятника при
его движении из положения С в положение
Д?
 .
Длину математического маятника
уменьшили в 2 раза. Как изменился период
колебания маятника?
.
Длину математического маятника
уменьшили в 2 раза. Как изменился период
колебания маятника? .
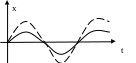
Чем отличаются две волны, показанные
на графике?
.
Чем отличаются две волны, показанные
на графике?