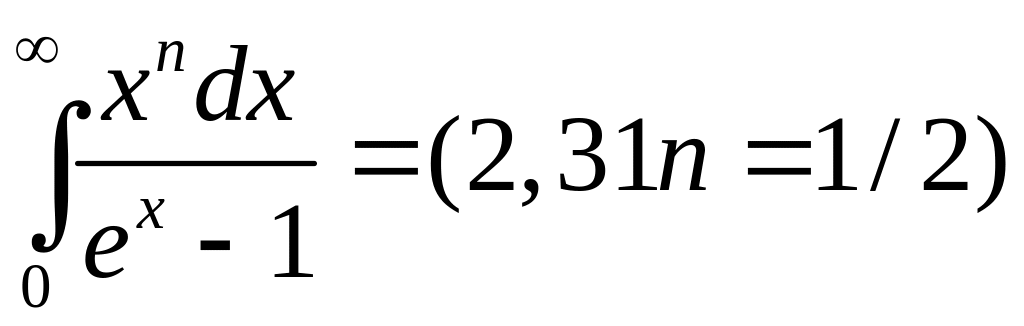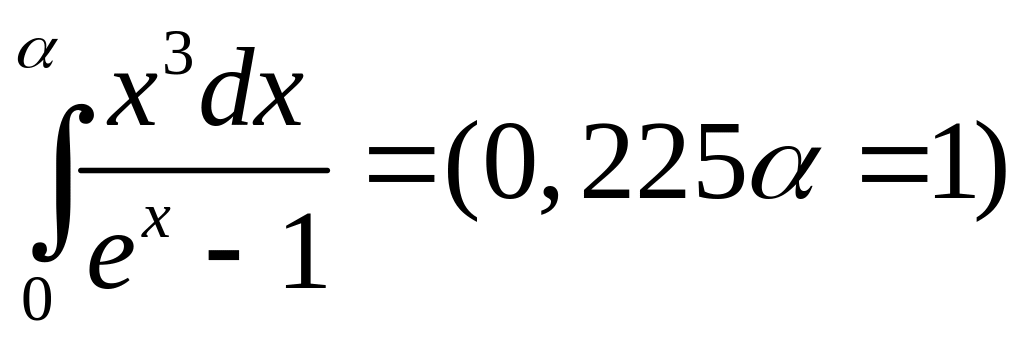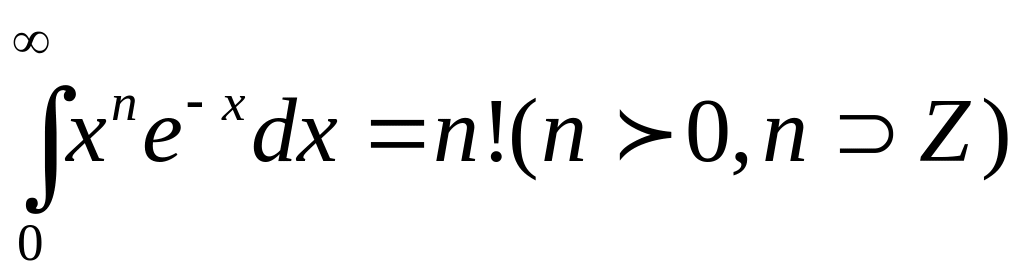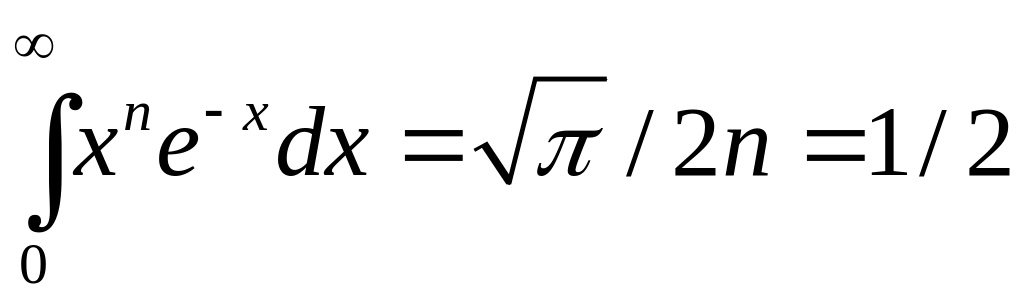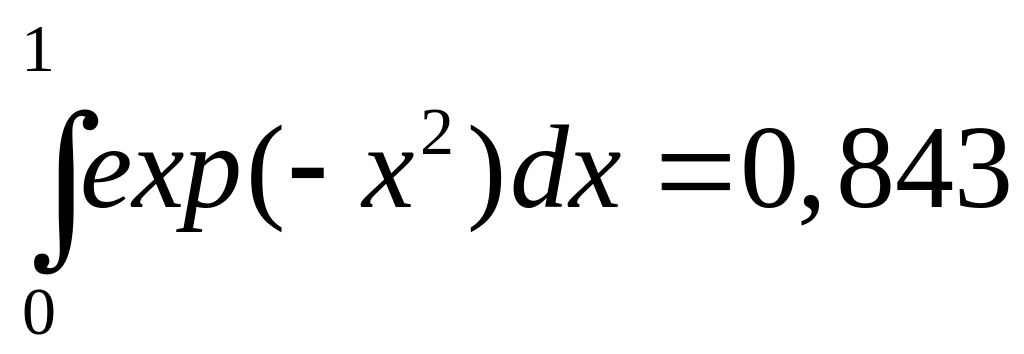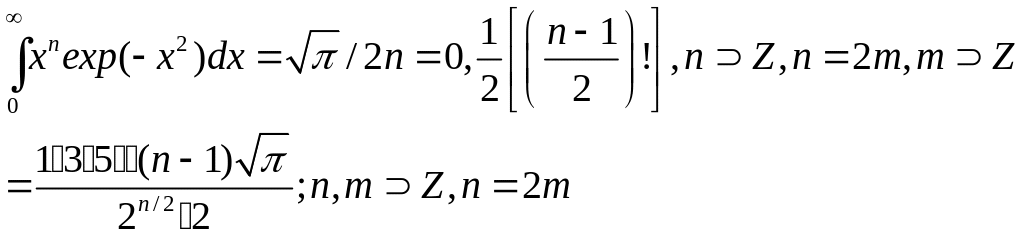3.2.Интегралы.

• Несобственные интегралы, встречающиеся в молекулярно-кинетической теории

• Н есобственный интеграл, встречающиеся в теории излучения абсолютно черного тела

• 

• 

• 

• 

• 

• Интегралы, встречающиеся в теории отражения плоских волн на плоской границе раздела прозрачных сред

R_II = 2

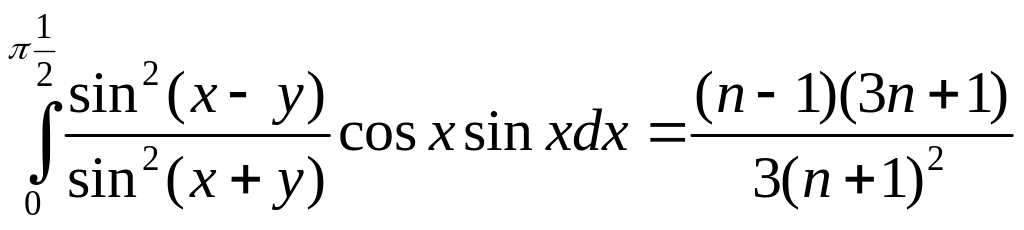
n = n₂/n₁ – относительный показатель преломления сред

(n₁ sin x = n₂ sin y).

5.3. Формулы для приближенных вычислений

(n – число верных знаков после запятой, величина h не должна превышать значения в таблице)

	n = 2	n = 3	n = 4
(1+h)2=1+2h	0.07	0.022	0.0007
(1+h)2=1+3h	0.04	0.012	0.004
1/(1+h)=1-h	0.06	0.022	0.007
(1+h)1/2=1+h/3	0.19	0.063	0.020
(1+h)1/3=1+h/3	0.2	0.068	0.021
lg(1+h)=0.4343h	0.14	0.047	0.015
lg((1+h)/(1-h))=2h	0.25	0.119	0.053
ln((1+h)/(1-h))	0.19	0.090	0.042
10k=1+2.30h	0.04	0.014	0.004
eh=1+h	0.09	0.031	0.010
sin(h)=h	17º	8º15'	3º50'
sin h = h-h3/6	51º	32º	20º
cos h = 1-h2/2	33º	18º	10º
cos h = 1	5º43'	1º48'	0º34'
tg h = h	14º	6º25'	3º02'
tg h = h+h/3	29º	18º	11º

(1 + h)ⁿ = 1 + nh; (1 + h)(1 ± q) = 1 + h ± q; (1 + h)(1 ± q) = 1 – h ± q; (1 + h)(1 ± q)(1 + z) = 1 + h ± q + z; 1/(1 ± h) = 1 ± h; (1 + h)/(1 + q) = 1 + h - q; (a ± h)ⁿ = aⁿ ± na^n-1 · h; a/(1 ± q) = a ± ah; ctg h = 1/h; (a² + h)^1/2 = (1/a) - (h/2a²); sin(φ ± h) = sin φ ± hcos φ; cos(φ ± h) = cos φ ± hsin φ; tg(φ ± h) = tgφ ± h/cos²φ; y(x + h) + y'(x)·h

В физике часто рассматривают треугольник специфического вида, в котором один угол гораздо меньше двух других.

Этот треугольник с малым углом при вершине используется в решении следующих задач:

- при расчете напряженности магнитного поля элемента тока. (Савельев, т.2. Рис. 42.2 с. 122 ) ;

- при расчете интерференционной картины (опыт Юнга) (Савельев, т.2. Рис. 119.2 с. 349);

- при расчете напряженности электростатического поля диполя (Савельев, т.2. Рис. 9.1 с. 29) .





₁

B

Проанализируем изображенный на рисунке треугольник АВР с малым углом  при вершине,.

Здесь приняты обозначения: АР = r₁, BP = r₂, PD = r, AC = r₁  r₂ = , AB = L.

Откладываем РВ = РС и, таким образом,  РВС равнобедренный, РK – медиана, биссектриса, высота, а угол

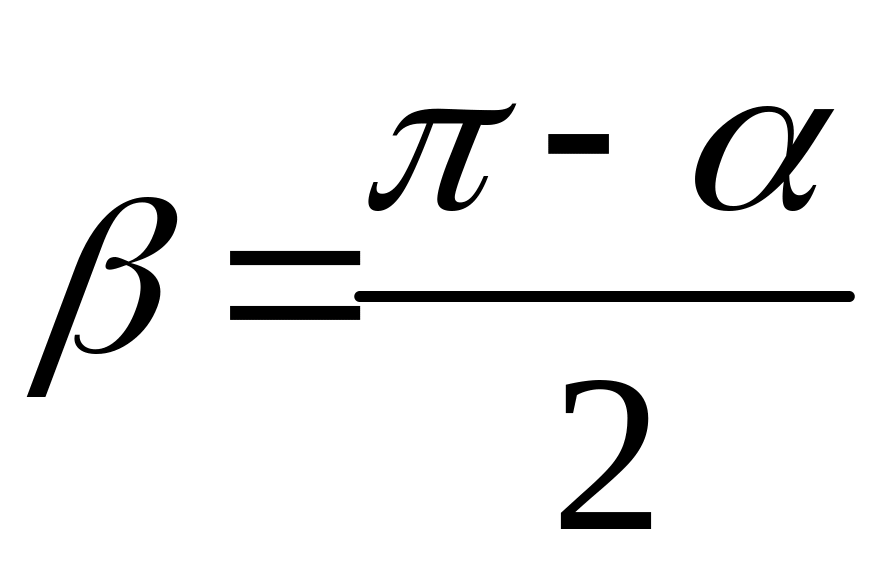
По условию угол  достаточно мал

При   0 угол  + ₂   и   ₁  

 CBA =     ( + ) =    ( + ) = ( + )

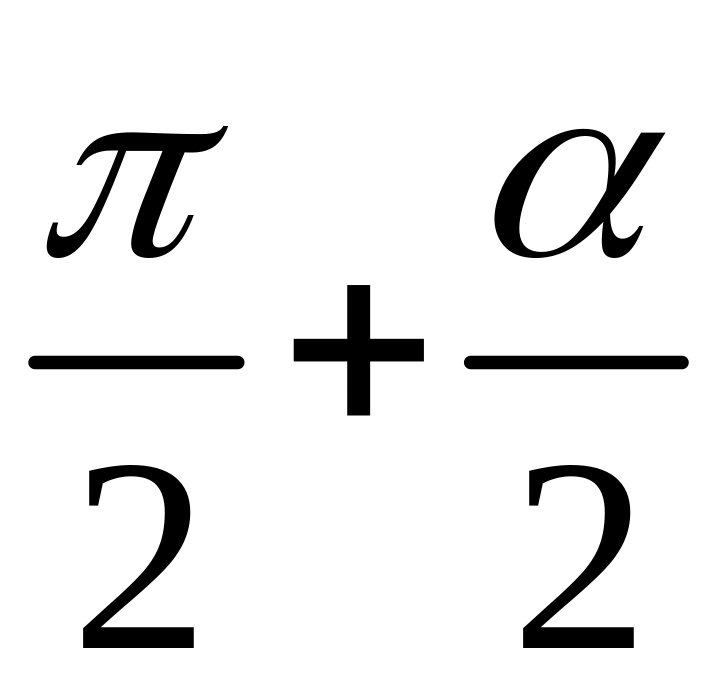
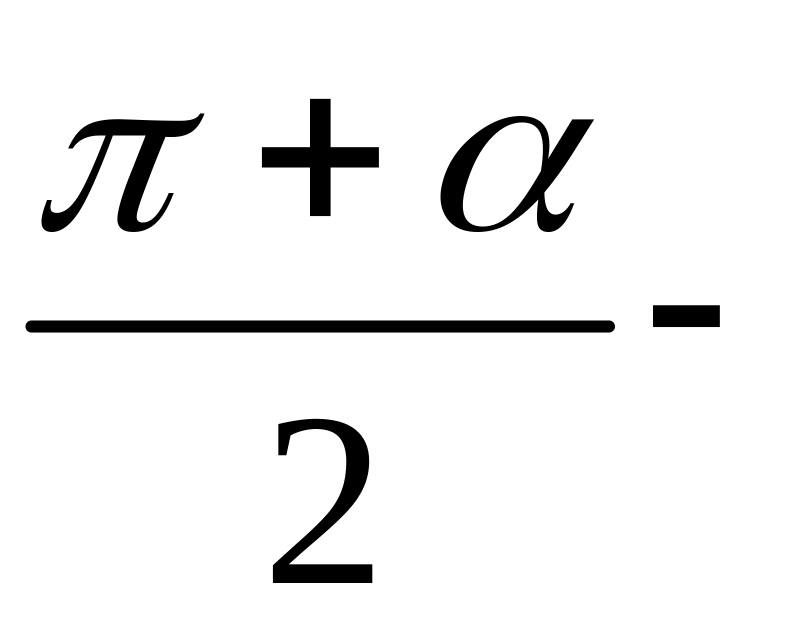 BСA =    =   0  BСA 

Таким образом,  BCР равнобедренный,  АСB - прямоугольный

 CBA =   

AC = AB  sin ( CBA) = AB  sin 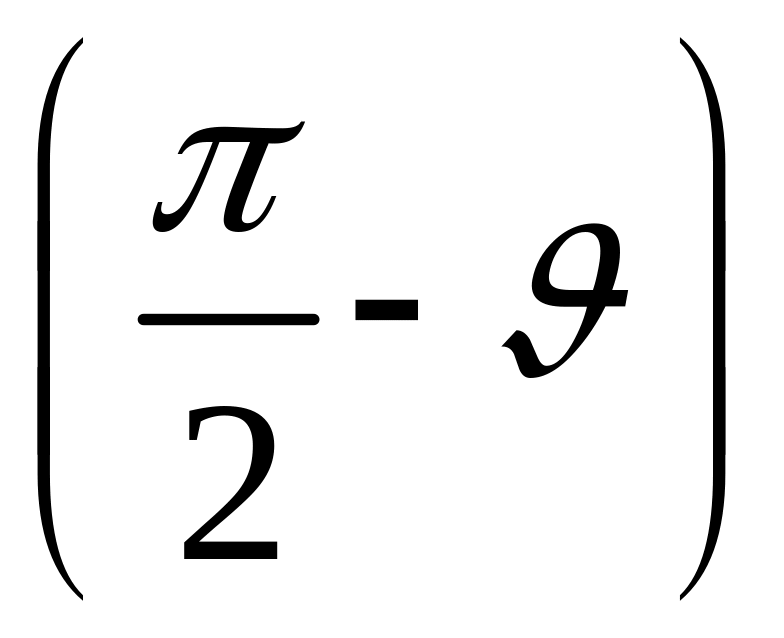= AB  cos 

 = AB  cos  = L  cos .

 РAB  + (  ) + (  ) = ;    =  + ; отсюда  = ,  РBB = +  =  +  . Отсюда  = .