2.3.7Расчет средних величин

Средняя арифметическая невзвешенная

,

.

Средняя арифметическая взвешенная

,

.

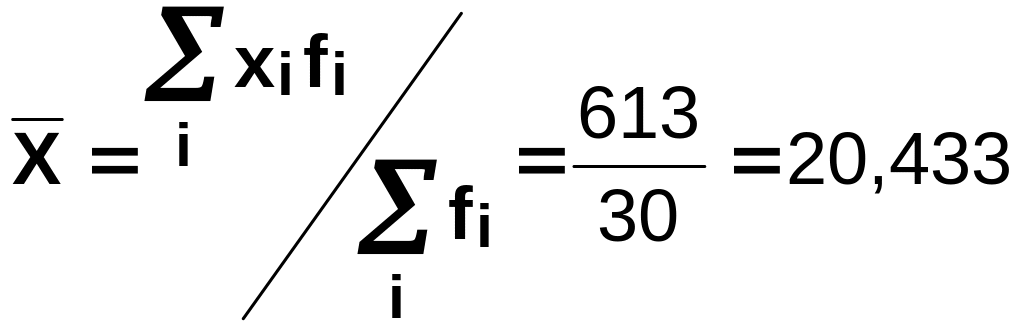Средняя гармоническая невзвешенная

,

.

Средняя гармоническая взвешенная

,

.

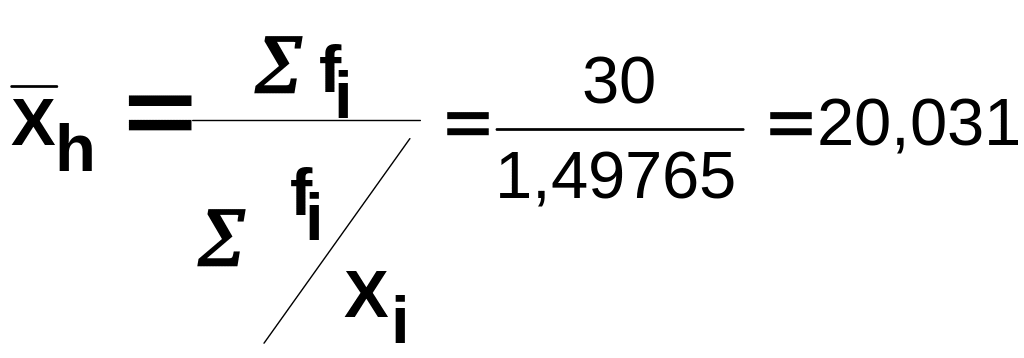2.3.8Выбор формы средней

Выполнение операции зависит от поставленной задачи, для которой необходимо вычислить среднюю, и от характера связи.

Для прямой зависимости вычисляют среднюю арифметическую, а для обратной – среднюю гармоническую.

Убедимся на примере. Допустим, необходимо определить объем продукции пяти заводов Q, используя информацию о средних трудозатратах на изделие и суммарную величину годовой трудоемкости работ Т:

.

В качестве исходных данных можно взять одну из строчек статистической табл. 3 (например, первую), где по пяти предприятиям представлена информация о выработке на одного рабочего, трудозатраты на изделие t и выработка Y имеют обратно пропорциональную зависимость. Найдем трудозатраты

,

где Ф – годовой фонд времени рабочего (примем Ф=1800 ч/год),

Y_i – выработка (изделий/год) по i-му заводу.

Результаты расчетов представим в виде таблицы.

Таблица 2.9

i	Предприятие	Yi	ti	Qi
1 2 3 4 5	Заря Восход Луч Маяк Эра	10 20 13 10 15	180 90 138,46 180 120	1000 2000 1300 1000 1500
	Итого	68		6800

Средние арифметические трудозатраты .

Проверим пригодность такой средней. Пусть в качестве годовой трудоемкости по каждому предприятию будет одинаковая величина, т.е. Т₁=Т₂=Т₃=Т₄=Т₅=180000 часов. Тогда, учитывая реальную производительность труда, можно определить годовой объем продукции Q_i в натуральном измерении по каждому i–му предприятию:

.

Результаты расчетов занесем в табл. 9

Объем продукции по всем предприятиям

Если средняя правильная, то справедливо будет следующее равенство:

,

.

Вывод: средняя арифметическая в данном случае неприменима. Поскольку зависимость объема продукции от трудозатрат обратная, то здесь следует использовать среднюю гармоническую.

Средняя гармоническая для нашего примера

.

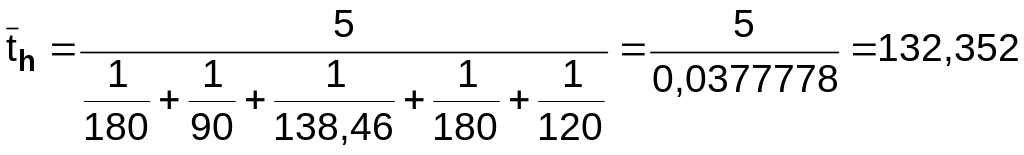Проверим, подходит ли средняя. Она подходит, поскольку

.

Таким образом, для расчетов объема продукции через среднюю трудозатрат необходимо пользоваться средней гармонической.

Через выработку у можно также определить объем продукции Q, но для этого следует использовать численность работающих N, которая связана с фондом времени рабочего Ф.

.

Тогда Средняя арифметическая ,

.

Вывод: так как зависимость Q(Y) прямая, то в данном случае нужно использовать среднюю арифметическую.

2.3.9Определение моды и медианы

Мода – вариант, наиболее часто встречающийся в статистическом ряду.

Для выработки Y (см. табл. 2.8) по ранжированному ряду видим, что чаще всего встречается вариант Y=24. Таким образом, М₀=24 имеет наибольшую частоту f.

Медиана – величина, которая делит ряд на две равные половины. Ее можно определить только по ранжированному ряду.

Рассмотрим ряд Y (см. табл. 2.8), в котором 18 членов. Теоретически медиана должна быть между 9-м и 10-м членами ряда, чтобы сумма накопленных частот (домедианная и послемедианная) равнялась .

Поскольку , то домедианная сумма частот должна равняться 15, следовательно, медианный интервал ряда 22-23. Для четных совокупностей можно взять среднее арифметическое крайних членов медианного ряда. Таким образом,

.

Средняя арифметическая, мода и медиана не совпадают, значит, вариационный ряд не имеет «нормального» распределения или оно не симметрично.