1. Кинематика поступательного движения материальной точки и вращательного движения твердого тела
Положение
материальной точки в пространстве
задается радиус-вектором
:
где
– единичные по модулю и взаимно
перпендикулярные векторы (орты системы
координат);
– координаты точки.
Средняя скорость
,
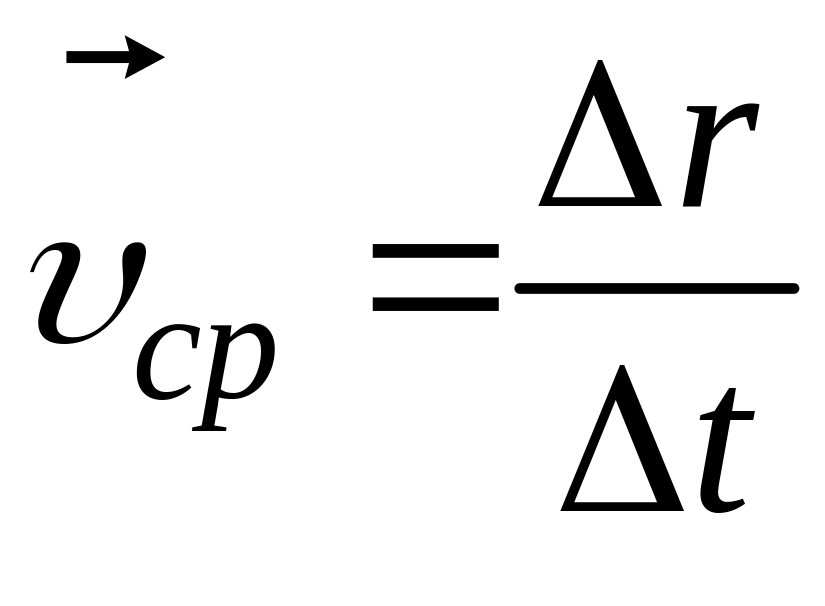где
– вектор перемещения материальной
точки за интервал времени
.
Мгновенная скорость
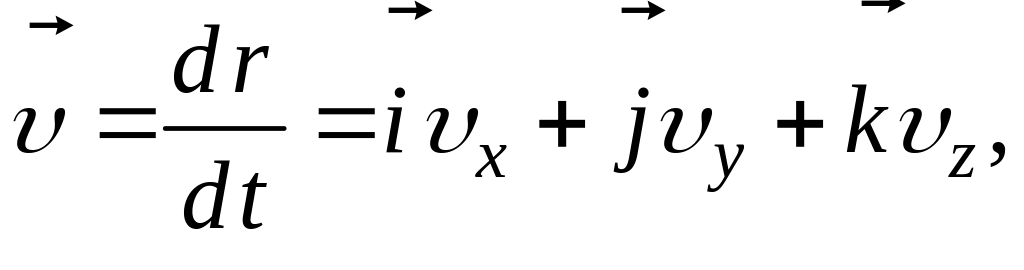
где
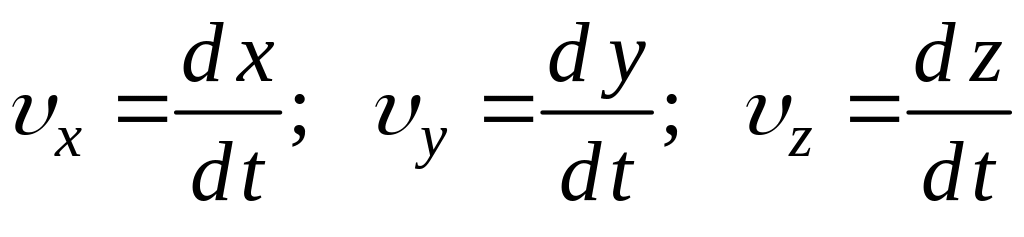– проекции вектора скорости
на оси координат.
Модуль скорости
Ускорение материальной точки
где
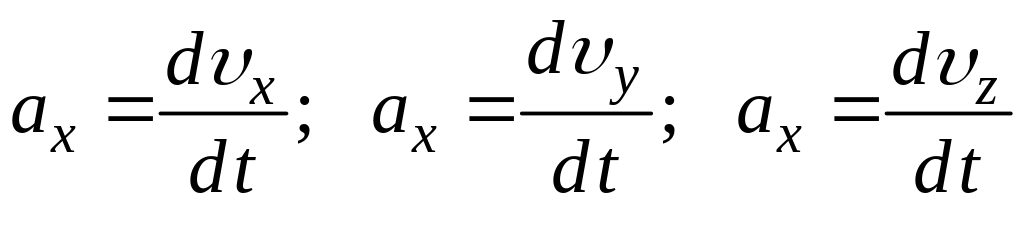– проекции вектора ускорения
на оси координат.
Модуль ускорения
При криволинейном движении материальной точки вектор ускорения
где
– нормальная составляющая;
– тангенциальная составляющая вектора
ускорения.
Модуль ускорения
где
– радиус кривизны траектории в данной
точке.
Равномерное
движение материальной точки вдоль оси
где
– координата в момент времени
.
Равноускоренное движение материальной точки вдоль оси
,
,
,
где
– координата и скорость в момент времени
.
При заданной оси
вращения положение твердого тела
определяется углом поворота
.
Средняя угловая скорость
где
– приращение угла поворота за время
.
Мгновенная угловая скорость
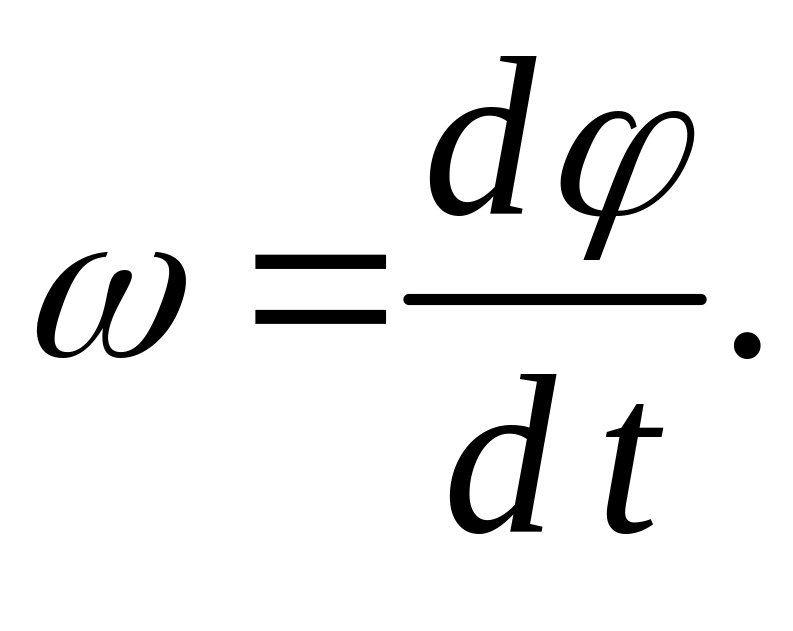
Угловое ускорение
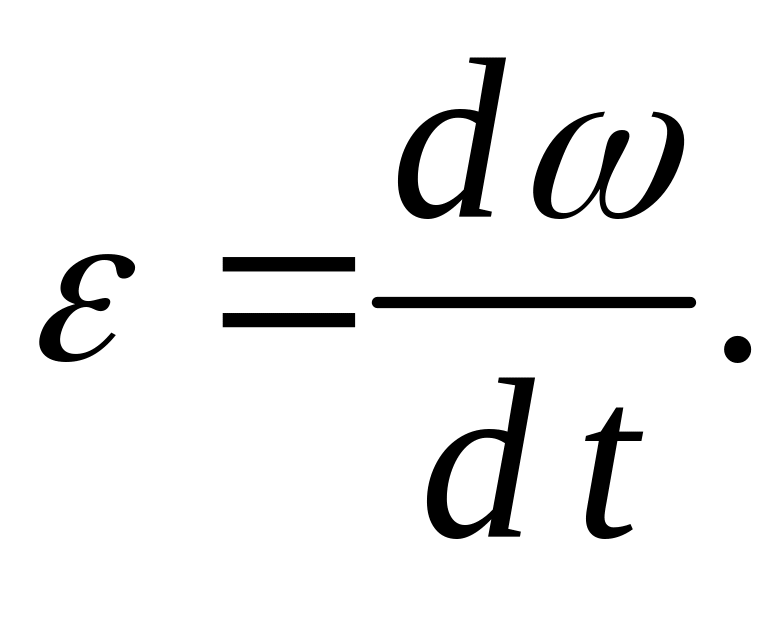
Равномерное вращение твердого тела
,
где
– начальное значение угла поворота.
Равноускоренное вращение твердого тела
,
,
где
– начальная угловая скорость.
Линейная скорость материальной точки, движущейся по окружности,
где
– угловая скорость,
– радиус окружности.
Тангенциальное ускорение
где
– угловое ускорение.
Нормальное ускорение
.
2. Динамика поступательного движения тела
Второй закон Ньютона (уравнение движения материальной точки):
где
– масса;
– ускорение;
– геометрическая сумма сил, действующих
на материальную точку.
Сила упругости для продольного растяжения или сжатия
где
– коэффициент упругости;
– абсолютная деформация.
Сила гравитационного
притяжения двух материальных точек
и
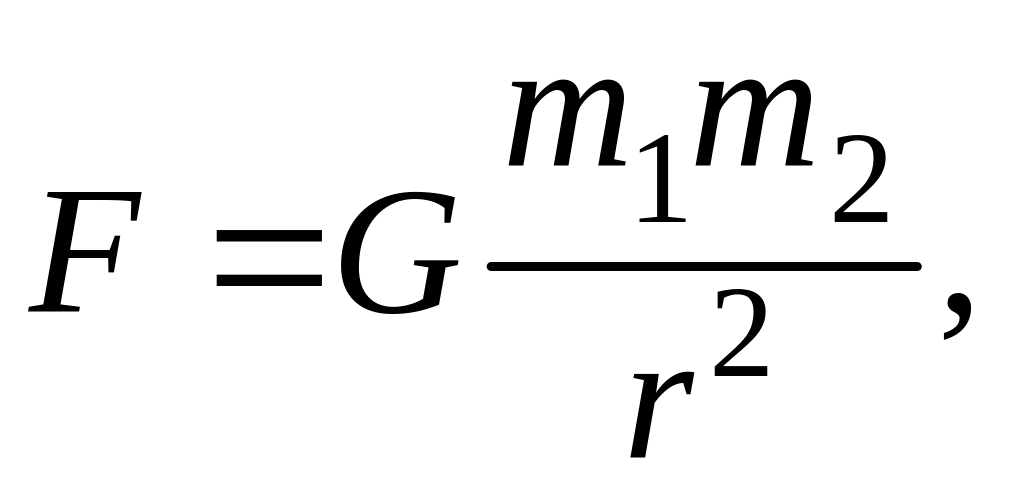
где
– гравитационная постоянная;
– расстояние между материальными
точками.
Сила трения скольжения
где
– коэффициент трения скольжения;
– сила реакции опоры (сила нормального
давления).
Координаты центра масс системы материальных точек
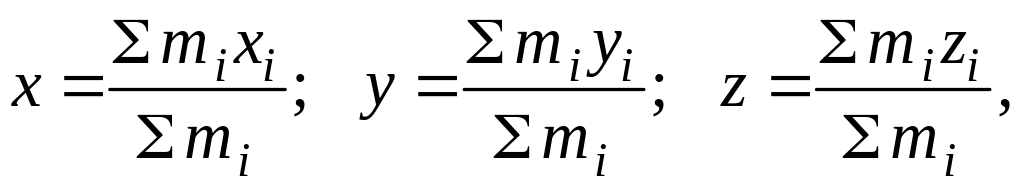
где
– масса
-й
материальной точки;
– координаты.
Закон сохранения импульса для замкнутой системы:
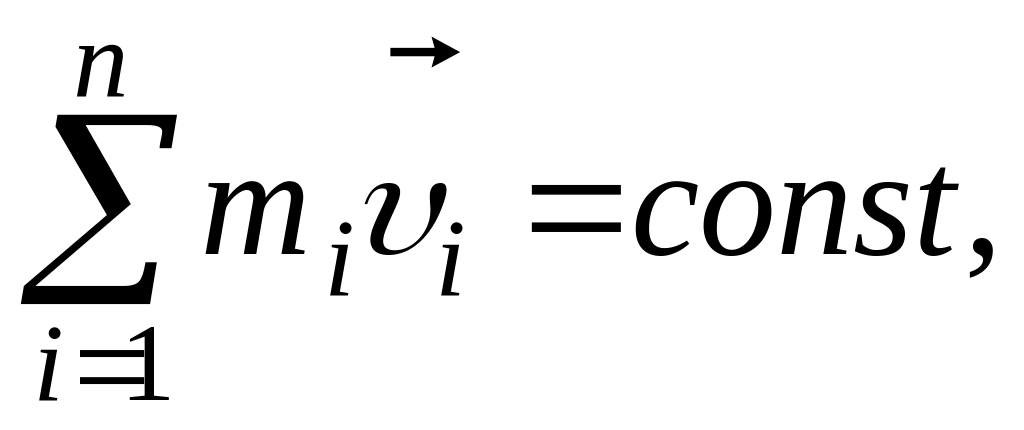
где
– число материальных точек, входящих
в систему;
,
– масса, скорость
-й
материальной точки.
Механическая работа, совершаемая силой,
где
– угол между направлениями векторов
силы
и перемещения
.
Интегрирование ведется вдоль траектории
движения.
Кинетическая энергия материальной точки
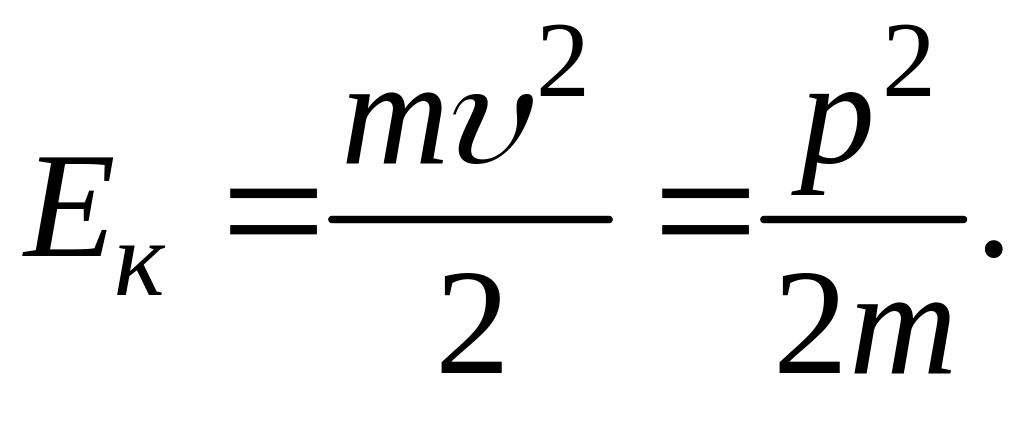
Потенциальная энергия тела при его продольном растяжении или сжатии
Потенциальная
энергия гравитационного взаимодействия
двух материальных точек массами
и
,
находящихся на расстоянии
друг от друга,
Потенциальная энергия и сила, действующая на частицу в данной точке поля, связаны уравнением
,
или
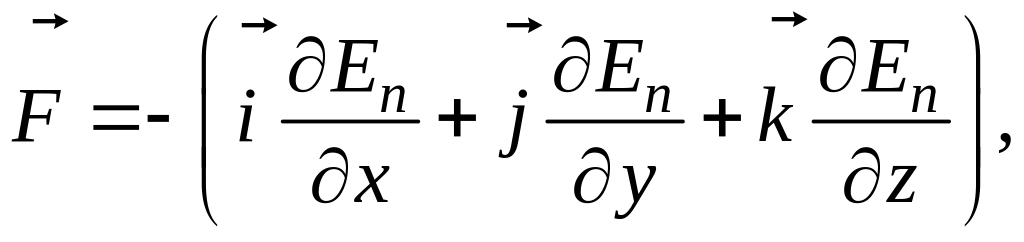
где
– орты системы координат;
,
,
– частные производные потенциальной
энергии по координатам
соответственно.
Полная механическая энергия замкнутой системы, в которой действуют только консервативные силы, сохраняется (закон сохранения механической энергии).
