1 Уравнения аэродинамики больших скоростей
1.1 Уравнение Бернулли для сжимаемого газа
Рассмотрим идеальное течение газа без вязкости. Кроме того, будем считать газ легким, следовательно, в нем будут отсутствовать массовые силы.
В потоке газа выделим элементарную струйку, ограниченную трубкой тока (рис.1.1). Здесь нужно вспомнить эти понятия основ аэродинамики и динамики полета.
Линия тока – кривая в потоке газа, в каждой точке которой вектор скорости в данный момент времени направлен по касательной.
Трубка тока – поверхность, образованная линиями тока, проведенными через все точки произвольного замкнутого контура площадью dS. Трубка тока считается непроницаемой для воздушных частиц.
Элементарная струйка – часть потока газа, ограниченная трубкой тока.
В связи с этим можно считать, что поток газа состоит из совокупности элементарных струек.
Рис.1.1 Элементарная струйка в потоке газа
Запишем для элементарной струйки 2-ой закон Ньютона
, (1.1)
который показывает, что произведение массы (газа) на ускорение равно сумме всех сил, действующих на тело (в данном случае – элементарную струйку). Проведем анализ данного уравнения (рис.1.2).
Рис.1.2 К выводу уравнения Бернулли для потока сжимаемого газа
В правой части уравнения (1.1) на элементарную струйку действуют силы давления по площадкам dS1, и dS2 , которые можно считать равными
.
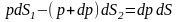По боковым поверхностям элементарной струйки силами давления пренебрегаем, так как они взаимно уравновешиваются. Силами трения (идеальный газ) и силами тяжести (легкий газ) также пренебрегаем.
Тогда
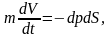или учитывая
,
.
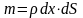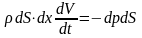Учитывая
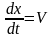и сокращая на dS, имеем
.
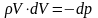Перенося – dp в левую часть
уравнения, и разделив обе части уравнения
на
,
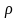получим
.
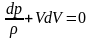(1.2)
Внося скорость V под знак дифференциала, получим
.
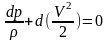(1.3)
Уравнения (1.2) и (1.3) являются двумя формами записи уравнения Бернулли для газа в дифференциальном виде. Вспомним, что в основе уравнения Бернулли лежит закон сохранения энергии.
Современные магистральные ВС (Ту-204, Airbus A320 и др.) летают с достаточно большими скоростями. При числах Маха М>0,4 плотность газа начинает изменяться, и движение газа уже нельзя считать движением несжимаемой жидкости.
Чтобы найти конечные величины p и V или связь между этими параметрами в дифференциальном уравнении Бернулли, необходимо проинтегрировать уравнение (1.3)
.
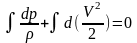(1.4)
Для сжимаемого течения зависимость между p и (без определения которой нельзя выполнить интегрирование) имеет вид
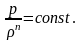
Для изоэнтропного (энтропия S не меняется), энергоизолированного (над газом не совершается работа) течения вместо показателя политропы n можно подставить k, и тогда интегрирование уравнения (1.4) можно выполнить.
В случае сжимаемого газа, когда плотность газа уже непостоянна, уравнение (1.4) после интегрирования преобразуется к виду
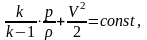(1.5)
где k – постоянная изоэнтропы (адиабаты) и для воздуха равна 1,4.
Это и есть уравнение Бернулли для потока сжимаемого газа.
Величина
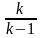в формуле (1.5) учитывает влияние
сжимаемости. Для газа как несжимаемой
жидкости при М<0,3….0,4 и =const,
k
и последнее уравнение имеет следующий
вид
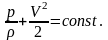
Заметим, что уравнение Бернулли при M ≤ 0,4 устанавливает связь между статическим давлением и скоростью в струйке.
Если умножить на плотность обе части уравнения, получим
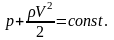
В результате имеем окончательную форму записи уравнения Бернулли для несжимаемого газа
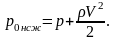(1.6)
Сравнивая формулы (1.5) и (1.6), приходим к выводу, что для измерения параметров сжимаемого течения газа (полет на больших скоростях) нужно вводить поправку на сжимаемость
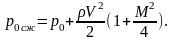
Величина
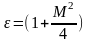показывает, что чем больше величина
скорости полета (М), тем больше поправка
на сжимаемость .
Если
воспользоваться соотношением, с помощью
которого определяется скорость звука
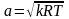или
,
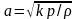и преобразовать первый член уравнения
(1.4), то получим формулу связи скорости
звука и скорости газа
Последняя форма записи нашла применение в теоретической аэродинамике (газодинамике).
Главный вывод уравнения Бернулли заключается в следующем: в потоке сжимаемого газа скорость и давление связаны обратно пропорциональной зависимостью.