Билет 1) Явление электромагнитной индукции.

что электрические токи создают вокруг себя магнитное поле. Связь магнитного поля с током привела к многочисленным попыткам возбудить ток в контуре с помощью магнитного поля. Эта фундаментальная задача была блестяще решена в 1831 г. английским физиком М. Фарадеем, открывшим явле­ние электромагнитной индукции, заключа­ющееся в том, что в замкнутом проводя­щем контуре при изменении потока маг­нитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.Опытным путем было также установ­лено, что значение индукционного тока совершенно не зависит от способа измене­ния потока магнитной индукции, а опреде­ляется лишь скоростью его изменения (в опытах Фарадея также доказывается, что отклонение стрелки гальванометра (сила тока) тем больше, чем больше ско­рость движения магнита, или скорость изменения силы тока, или скорость движе­ния катушек).Открытие явления электромагнитной индукции имело большое значение, так как была доказана возможность получе­ния электрического тока с помощью маг­нитного поля. Этим была установлена вза­имосвязь между электрическими и магнит­ными явлениями, что послужило в даль­нейшем толчком для разработки теории электромагнитного поля

Электродвижущаяся сила.возник­новение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой элек­тромагнитной индукции. Значение индук­ционного тока, а следовательно, и э. д. с, электромагнитной индукции ξ_i определя­ются только скоростью изменения магнит­ного потока, т. е.

Законы Фарадея-Ленца.выбирая опре­деленное положительное направление нор­мали, мы определяем как знак потока маг­нитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими пред­ставлениями и выводами, можно соответ­ственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватыва­емого замкнутым проводящим контуром, возникающая в контуре э.д.с.

Знак минус показывает, что увеличе­ние потока (dФ/dt>0) вызывает э.д.с.

ξξ_i<0, т. е. поле индукционного тока на­правлено навстречу потоку; уменьшение потока (dФ/dt<0 ) вызывает ξ_i>0,т. е. направления потока и поля индукци­онного тока совпадают. Знак минус в фор­муле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления ин­дукционного тока, выведенного в 1833 г. Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по­тока, вызвавшего этот индукционный ток.

2. Явление самоиндукции. Индуктивность тонкого соленоида. Единицы индуктивности. Ток при размыкании и замыкании цепи.

Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное по¬ле, индукция которого, по закону Био — Савара—Лапласа (см. (110.2)), пропор¬циональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорциона¬лен току I в контуре: Ф=LI, (126.1) где коэффициент пропорциональности L называется индуктивностью контура.

Возникновение э.д.с. индукции в прово¬дящем контуре при изменении в нем силы тока называется самоиндукцией.

Из выражения (126.1) определяется единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:

1 Гн=1 Вб/А=1В•с/А.

На примере соленоида: l,S,N,J, l>>d

Каждый виток соленоида создает магнитный поток Ф=B*S=|B=µ0NJ/l|= µ0NJS/l (1)

Суммарный магнитный поток. Создаваемый всеми витками соленоида (потокосцепление) Ф=NФ1=|= µ0N2JS/l=LJ (2)

εS=-dФ/dt=-LdJ/dt (3)

L=const, L= µ0NS/l (4)

Js= εS/R=-LdJ/Rdt (5)

Если ток со временем возрастает, то dJ/dt>0 и ξs<0, т. е. ток самоиндукции направлен навстречу току, обусловленно-му внешним источником, и тормозит его возрастание. Если ток со временем убывает, то dI/dt<0 и ξs>0, т. е. индукционный.

ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, об-ладая определенной индуктивностью, при¬обретает электрическую инертность, за¬ключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность контура.

Рассмотрим процесс выключения тока в цепи

В момент времени t=0 отключим источник тока. Ток через катушку индук¬тивности L начнет уменьшаться, что при¬ведет к возникновению э.д.с. самоиндук¬ции ξs=-LdI/dt, препятствующей, со¬гласно правилу Ленца, уменьшению тока.

Чем больше индуктивность цепи и меньше ее сопро¬тивление, тем больше т и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.

При замыкании цепи помимо внешней э.д.с.ξ возникает э.д.с. самоиндукции

ξs=-LdI/dt, препятствующая, согласно

правилу Ленца, возрастанию тока.

В момент замыкания (t=0) сила тока I=0 и u=-ξ.

Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.

L=εS/(dJ/dt ), dJ/dt=1А/с

Ф=LJ, L=Ф/J , L=(Гн)=(Вб/А). вб-вебер

Билет 3. Взаимная индукция. Энергия магнитного поля. Практическое применение электромагнитной индукции.

Взаимная индукция

Рассмотрим два контура, расположенных на малом расстоянии друг от друга.

Ф₂₁=L₂₁I₁, I₁ const

Ф₁₂=L₁₂I₂, I₂ const

Контуры 1 и 2 называются индуктивно связанными, а явление возникновения ЭДС в одном из контуров при изменениях силы тока в другом называется взаимной индукцией.

L₁₂=L₂₁ – коэффициенты взаимной индуктивности.

Энергия магнитного поля

Е сли ключ К перевести в положение 2, то через соленоид течет возрастающий ток за счет явления самоиндукции. Если ключ К перевести в положение 1, то в течение некоторого времени через лампу накаливания будет течь ток (явление самоиндукции).

dt dA= ₀*I*dt=| ₀=-L |=-L*I*dI (1)

A=- =W_m (2)

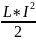W= (3)

(3) преобразуем применительно к тонкому соленоиду с учетом:

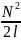L = ₀ S; B= ₀ I; W= ₀ S* =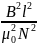

Найдем энергию единицы объема магнитного поля, т.е. объемную плотность магнитного поля

Практическое применение электромагнитной индукции.

Явление электромагнитной индукции используется, прежде всего, для преобразования механической энергии в энергию электрического тока. Для этой цели применяются генераторы переменного тока (индукционные генераторы).

Для промышленного производства электроэнергии на электрических станциях используются синхронные генераторы. Неподвижная часть синхронного генератора называется статором, а вращающаяся – ротором. Ротор генератора имеет обмотку постоянного тока (обмотку возбуждения) и является мощным электромагнитом. Постоянный ток, подаваемый на  обмотку возбуждения через щеточно-контактный аппарат, намагничивает ротор, и при этом образуется электромагнит с северным и южным полюсами.

На статоре генератора расположены три обмотки переменного тока, которые смещены одна относительно другой на 120⁰ и соединены между собой по определенной схеме включения.

При вращении возбужденного ротора с помощью паровой или гидравлической турбины его полюсы проходят под обмотками статора, и в них индуцируется изменяющаяся по гармоническому закону электродвижущая сила. Далее генератор по определенной схеме электрической сети соединяется с узлами потребления электроэнергии.

Если передавать электроэнергию от генераторов станций к потребителям по линиям электропередачи непосредственно (на генераторном напряжении, которое относительно невелико), то в сети будут происходить большие потери энергии и напряжения. Следовательно, для экономичной транспортировки электроэнергии необходимо уменьшить силу тока. Однако, так как передаваемая мощность при этом остается неизменной, напряжение должно  увеличиться во столько же раз, во сколько раз уменьшается сила тока.

У потребителя электроэнергии, в свою очередь, напряжение необходимо понизить до требуемого уровня. Электрические аппараты, в которых напряжение увеличивается или уменьшается в заданное количество раз, называются трансформаторами. Работа трансформатора также основана на законе электромагнитной индукции.

Билет 4. Намагничивание вещества. Магнитные характеристики вещества: вектор намагничивания, магнитная проницаемость, магнитная восприимчивость, напряженность магнитного поля. Циркуляция напряженности магнитного поля.

Для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнит­ным моментом единицы объема магнетика:

J=p_m/V=p_a/V,

где p_m=р_а— магнитный момент маг-нетика, представляющий собой векторную сумму магнитных моментов отдельных мо­лекул.

Магнитное поле макротоков описыва­ется вектором напряженности Н. Для од­нородной изотропной среды вектор маг­нитной индукции связан с вектором на­пряженности следующим соотношением:

В=₀Н

где ₀ — магнитная постоянная,  — без­размерная величина — магнитная прони­цаемость среды, показывающая, во сколь­ко раз магнитное поле макротоков Н уси­ливается за счет поля микротоков среды.

Намагниченность прямо пропорцио­нальна напряженности поля, вызывающе­го намагничение, т. е.

J=H, (133.6)

где  — безразмерная величина, называе­мая магнитной восприимчивостью вещества. Для диамагнетиков  отрицательна (поле молекулярных токов противополож­но внешнему), для парамагнетиков — по­ложительна (поле молекулярных токов со­впадает с внешним).

Цир­куляция вектора Н по произвольному за­мкнутому контуру L равна алгебраической сумме токов проводимости, охватывае­мых этим контуром:

Билет 5. Ферромагнетизм. Элементарные носители ферромагнетизма – электронные спины. Доменная теория ферромагнетизма. Намагничивание ферромагнетика. Магнитный гистерезис. Точка Кюри.

Сильномагнитные вещест­ва — ферромагнетики — вещества, обла­дающие спонтанной намагниченностью, т. е. они намагничены даже при отсутствии внешнего магнитного поля. К ферромагне­тикам кроме основного их представите­ля — железа (от него и идет название «ферромагнетизм») — относятся, напри­мер, кобальт, никель, гадолиний, их спла­вы и соединения.

Вейсс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри разбива­ется на большое число малых макроскопи­ческих областей — доменов, самопроиз­вольно намагниченных до насыщения. При отсутствии внешнего магнитного поля магнитные моменты отдельных до­менов ориентированы хаотически и ком­пенсируют друг друга, поэтому результи­рующий магнитный момент ферромагнети­ка равен нулю и ферромагнетик не намагничен. С ростом Н намагниченность J и магнитная индукции В уже в довольно слабых полях растут очень быстро. Эксперименты показа­ли, что зависимость В от J не является плавной, а имеет ступенчатый вид. Это свидетель­ствует о том, что внутри ферромагнетика домены поворачиваются по полю скачком. При ослаблении внешнего магнитного поля до нуля ферромагнетики сохраняют остаточное намагничение, так как тепло­вое движение не в состоянии быстро дезо­риентировать магнитные моменты столь крупных образований, какими являются домены. Поэтому и наблюдается явление магнитного гистерезиса. Для того чтобы ферромагнетик размагнитить, необходимо приложить коэрцитивную си­лу; размагничиванию способствуют также встряхивание и нагревание ферромагнети­ка. Точка Кюри оказывается той темпера­турой, выше которой происходит разруше­ние доменной структуры.

По мере возрастания Н намагниченность J сначала растет быст­ро, затем медленнее и, наконец, достигает­ся так называемое магнитное насыщение J_нас, уже не зависящее от напряженности поля. Подобный характер зависимости J от H можно объяснить тем, что по мере увеличения намагничивающего поля уве­личивается степень ориентации молеку­лярных магнитных моментов по полю, од­нако этот процесс начнет замедляться, когда остается все меньше и меньше нео­риентированных моментов, и, наконец, когда все моменты будут ориентированы по полю, дальнейшее увеличение J пре­кращается и наступает магнитное насы­щение. График зависимости J от Н называется магнитным гистерезисом.

Напряженность H_C называется ко­эрцитивной силой.

Для каждого ферромагнетика имеется определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. При нагревании образца выше точки Кюри ферромагнетик превращается в обычный парамагнетик. Переход вещест­ва из ферромагнитного состояния в пара­магнитное, происходящий в точке Кюри, не сопровождается поглощением или выделением теплоты

Билет 6. Обобщение закона электромагнитной индукции. Первое уравнение Максвелла.

Максвелл высказал гипотезу, что всякое переменное магнит­ное поле возбуждает в окружающем про­странстве электрическое поле, которое и является причиной возникновения ин­дукционного тока в контуре, циркуляция которого равна изменению магнитного потока:

Подставив в формулу (137.1) выраже­ние (см. (120.2)), получим

Если поверхность и контур неподвиж­ны, то операции дифференцирования и ин­тегрирования можно поменять местами. Следовательно,

циркуляция вектора напряженности электростатического поля (обозначим его e_q) вдоль любого замкну­того контура равна нулю:

Сравнивая выражения (137.1) и (137.3), видим, что между рассматриваемыми по­лями (Е_B и e_q) имеется принципиальное различие: циркуляция вектора Е_B в отли­чие от циркуляции вектора e_q не равна нулю. Следовательно, электрическое поле Е_B, возбуждаемое магнитным полем, как и само магнитное поле, явля­ется вихревым.

Вывод первого уравнения Максвелла.

Сравнивая это выражение с I=I_см = , имеем

D=₀E+P, где Е — напряжен­ность электростатического поля, а Р — поляризованность (см. § 88), то плотность тока смещения

где ₀дE/дt — плотность тока смещения

Плотность полного тока j_полн=j+дD/дt.

I_полн=

первое уравнение Максвелла

7. Для установления количественных отношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.

Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор «протекают» токи смещения, причем в тех участках, где отсутствуют проводники

электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток смещения, равный току в подводящих проводах. Тогда можно утверждать, что токи проводимости (/) и смещения (/см ) рав-ны: Ток проводимости вблизи обкладок (в общем случае).

плотность тока смещения

При зарядке конденсатора (рис. 199, а) через провод- ник, соединяющий обкладки, ток течет от правой обкладки к левой, поле в конденсаторе усиливается, следовательно, т. е. вектор направлен в ту же сторону, что и D.

При разрядке конденсатора (рис. 199, б) через проводник, соединяющий обкладки, ток течет от левой обкладки к правой, поле в конденсаторе ослабляется; следовательно, т. е. вектор направлен противоположно в ектору D направление вектора j, а следовательно, и вектора j_см совпадает

с направлением вектора дD/дt

Максвелл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле

диэлектриках ток смещения:

Максвелл ввел понятие полного тока, равного сумме токов проводимо- сти (а также конвекционных токов) и смещения. Плотность полного тока j_полн=j+дD/дt.

Максвелл обобщил теорем}' о циркуляции вектора Н , введя в ее правую часть полный ток I_полн= поверхность S, натянутую на замкнутый контур L. Тогда обобщенная теорема о циркуляции вектора Н запишется в виде

Второе уравнение Максвелла - это обобщение закона индукции Фарадея для диэлектрической среды в свободном пространстве

Физический смысл второго уравнения Максвелла состоит в том, что электрическое поле в некоторой области пространства связано с изменением магнитного поля во времени в этой области. То есть переменное магнитное поле возбуждает вихревое электрическое поле.

Получим второе уравнение Максвелла в интегральной форме

Уравнение 1.19 – второе уравнение Максвелла в интегральной форме.

 

Уравнение 1.20 есть второе уравнение Максвелла в дифференциальной форме.