МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ

Практическая работа №3

«Симплекс-метод»

по дисциплине

«Теория принятия решений»

Студент

Филатов А.А.

подпись, дата

фамилия, инициалы

Группа

АС-09

Принял

Корнеев А.М.

ученая степень, звание

подпись, дата

фамилия, инициалы

Липецк 2012

1. Задание

1. Решить задачу линейного программирования используя итерации симплекс-метода.

2. Построение исходной симплекс-таблицы.

3. Проверка полученного базисного плана на оптимальность по условию оптимальности.

4. Осуществление перехода к новому базисному плану.

5. Выполнение процедуры замены базиса.

6. Реализация алгоритма симплекс-метода.

2. Решение

Целевая функция имеет вид: .

А область ограничений задачи в стандартной форме имеет вид:

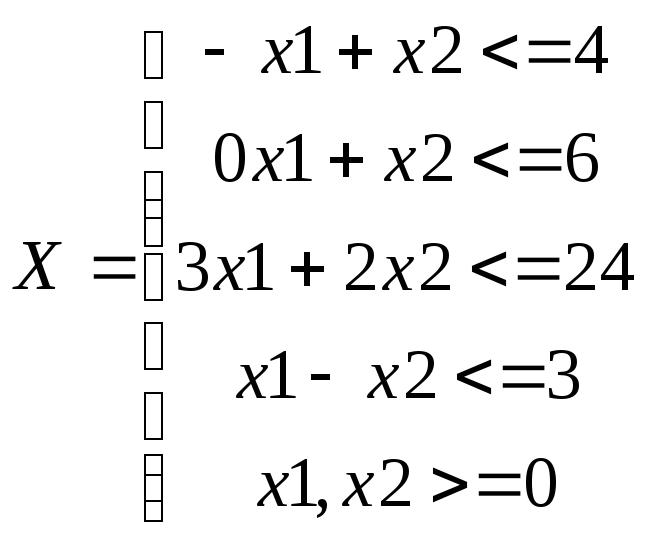
Найденное оптимальное решение в предыдущих практических работах:

.

Приведем исходную задачу к канонической форме:

Среди переменных задачи можно выделить базисные переменные: и не базисные: .

Итерация 0

Базис	B
	4	-1	1	1	0	0	0
	6	0	1	0	1	0	0
	24	3	2	0	0	1	0
	3	1	-1	0	0	0	1
	0	-5	-7	0	0	0	0

Проверим полученный базисный план на оптимальность по условию оптимальности: В симплекс-таблице есть отрицательные коэффициенты строки , значит данное ДБР не оптимально.

Для перехода к новому базисному плану из числа небазисных переменных с отрицательными значениями выбирается переменная, которая вводится в базис, это переменная , которой соответствует наибольшая по абсолютной величине отрицательная оценка.

Ведущий столбец: .

Выбираем переменную, которая выводится из базиса. Для элементов ведущего столбца, которые больше 0, находим .

Ведущая строка: .

Ведущий элемент: 1.

Итерация 1

Базис	B
	4	-1	1	1	0	0	0
	2	1	0	-1	1	0	0
	16	5	0	-2	0	1	0
	7	0	0	1	0	0	1
	28	-12	0	7	0	0	0

Проверим полученный базисный план на оптимальность по условию оптимальности: В симплекс-таблице есть отрицательные коэффициенты строки , значит данное ДБР не оптимально.

Для перехода к новому базисному плану из числа небазисных переменных с отрицательными значениями выбирается переменная, которая вводится в базис, это переменная , которой соответствует наибольшая по абсолютной величине отрицательная оценка.

Ведущий столбец: .

Выбираем переменную, которая выводится из базиса. Для элементов ведущего столбца, которые больше 0, находим .

Ведущая строка: .

Ведущий элемент: 1.

Итерация 2

Базис	B
	6	0	1	0	1	0	0
	2	1	0	-1	1	0	0
	6	0	0	3	-5	1	0
	7	0	0	1	0	0	1
	52	0	0	-5	12	0	0

Проверим полученный базисный план на оптимальность по условию оптимальности: В симплекс-таблице есть отрицательные коэффициенты строки , значит данное ДБР не оптимально.

Для перехода к новому базисному плану из числа небазисных переменных с отрицательными значениями выбирается переменная, которая вводится в базис, это переменная , которой соответствует наибольшая по абсолютной величине отрицательная оценка.

Ведущий столбец: .

Выбираем переменную, которая выводится из базиса. Для элементов ведущего столбца, которые больше 0, находим .

Ведущая строка: .

Ведущий элемент: 3.

Итерация 3

Базис	B
	6	0	1	0	1	0	0
	4	1	0	0	-2/3	1/3	0
	2	0	0	1	-5/3	1/3	0
	5	0	0	0	5/3	-1/3	1
	62	0	0	0	11/3	5/3	0

Проверим полученный базисный план на оптимальность по условию оптимальности: В симплекс-таблице все коэффициенты строки неотрицательные, значит данное ДБР оптимально.

Таким образом, .