
Практическая работа №4 Вариант 17
.docМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ
Практическая работа №4
«Анализ линейных моделей на чувствительность.
Двойственный симплекс-метод»
по дисциплине
«Теория принятия решений»
|
|
Студент |
|
|
|
Филатов А.А. |
|
||||||||
|
|
|
|
подпись, дата |
|
фамилия, инициалы |
|
||||||||
|
|
Группа |
|
АС-09 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
Принял |
|
|
|
|
|
||||||||
|
|
|
|
|
|
Корнеев А.М. |
|
||||||||
|
|
ученая степень, звание |
|
подпись, дата |
|
фамилия, инициалы |
|
||||||||
Липецк 2012
1. Задание
Проанализировать имеющуюся линейную модель на чувствительность, используя двойственный симплекс - метод.
Порядок выполнения работы:
1. Исходными данными взять результаты, посчитанные симплекс-методом.
2. Ввести новые ограничения и реализовать двойственный симплекс-метод.
3. Оценить активные, пассивные и избыточные ограничения.
2. Решение
Целевая функция
имеет вид:
![]() .
.
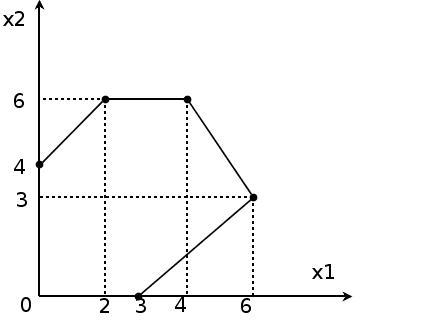
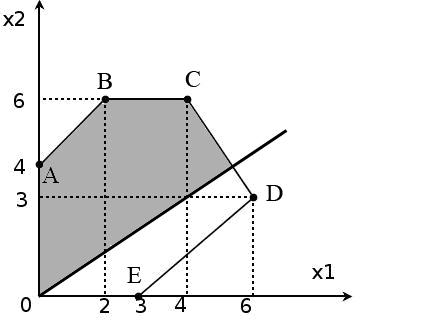
А область ограничений задачи в стандартной форме имеет вид:
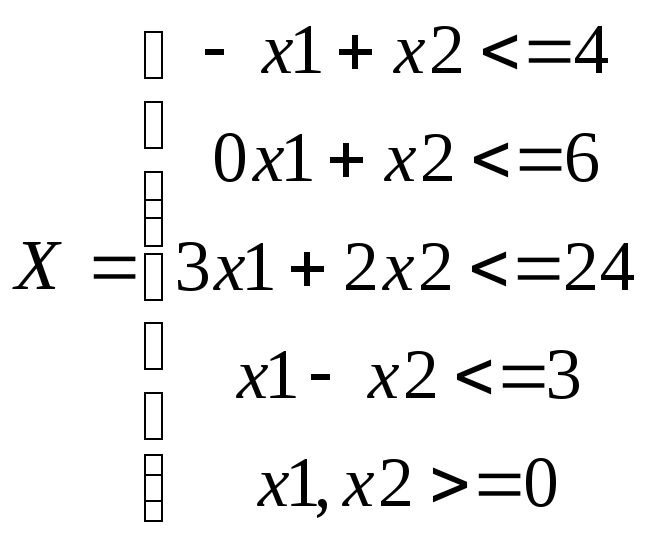
Найденное оптимальное решение в предыдущих практических работах:
![]() .
.
Симплекс-таблица, полученная в практической работе №3 имеет вид:
|
Базис |
B |
|
|
|
|
|
|
|
|
6 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
4 |
1 |
0 |
0 |
-2/3 |
1/3 |
0 |
|
|
2 |
0 |
0 |
1 |
-5/3 |
1/3 |
0 |
|
|
5 |
0 |
0 |
0 |
5/3 |
-1/3 |
1 |
|
|
62 |
0 |
0 |
0 |
11/3 |
5/3 |
0 |
1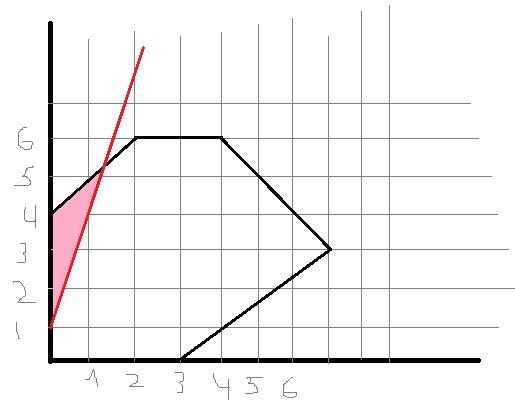 )
Введем дополнительное ограничение:
)
Введем дополнительное ограничение:
Уравнение прямой имеет вид:
-3x1+x2=1
Ограничение имеет вид:
3x1-x2<=-1
Представим в канонической форме:
3x1-x2+x7=-1.
Выразим x2: x2=6-x4.
Выразим x1: x1=4+2/3x4-1/3x5
Формируем новую строку симплекс таблицы:
3x4-x5+x7=-3.
|
Базис |
B |
|
|
|
|
|
|
|
|
|
6 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
|
4 |
1 |
0 |
0 |
-2/3 |
1/3 |
0 |
0 |
|
|
2 |
0 |
0 |
1 |
-5/3 |
1/3 |
0 |
0 |
|
|
5 |
0 |
0 |
0 |
5/3 |
-1/3 |
1 |
0 |
|
|
-7 |
0 |
0 |
0 |
3 |
-1 |
0 |
1 |
|
|
62 |
0 |
0 |
0 |
11/3 |
5/3 |
0 |
0 |
Проверим полученный базисный план на оптимальность по условию оптимальности: В симплекс-таблице в столбце базисных переменных есть отрицательные элементы, значит данное базисное решение не оптимально.
Выбираем переменную,
которая выводится из базиса. Находим
строку, у которой самый большой по модулю
отрицательный элемент
![]() .
.
Ведущая строка:
![]() .
.
Выбираем переменную,
которая вводится в базис. Для элементов
ведущей строки, которые меньше 0, находим
![]() .
.
Ведущий столбец:
![]() .
.
Перестроим симплекс-таблицу по правилам обычного симплекс-метода:
|
Базис |
B |
|
|
|
|
|
|
|
|
|
6 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
|
3 |
1 |
0 |
0 |
1/3 |
1/3 |
0 |
1/3 |
|
|
1 |
0 |
0 |
1 |
-2/3 |
1/3 |
0 |
1/3 |
|
|
6 |
0 |
0 |
0 |
2/3 |
-1/3 |
1 |
-1/3 |
|
|
3 |
0 |
0 |
0 |
3 |
-1 |
0 |
1 |
|
|
57 |
0 |
0 |
0 |
26/3 |
5/3 |
0 |
5/3 |
Проверим полученный базисный план на оптимальность по условию оптимальности: В симплекс-таблице в столбце базисных переменных нет отрицательных элементов, значит данное базисное решение оптимально.
Значение целевой функции ухудшилось по сравнению с исходным оптимальным решением, следовательно, дополнительное ограничение АКТИВНОЕ.
2) Введем дополнительное ограничение:
Уравнение прямой имеет вид:
3x1-4x2=0
Ограничение имеет вид:
3x1-4x2<=0
Представим в канонической форме:
3x1-4x2+x7=0
Выразим x2: x2=6-x4.
Выразим x1: x1=4+2/3x4-1/3x5
Формируем новую строку симплекс таблицы:
6x4-x5+x7=12
|
Базис |
B |
|
|
|
|
|
|
|
|
|
6 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
|
4 |
1 |
0 |
0 |
-2/3 |
1/3 |
0 |
0 |
|
|
2 |
0 |
0 |
1 |
-5/3 |
1/3 |
0 |
0 |
|
|
5 |
0 |
0 |
0 |
5/3 |
-1/3 |
1 |
0 |
|
|
12 |
0 |
0 |
0 |
6 |
-1 |
0 |
1 |
|
|
62 |
0 |
0 |
0 |
11/3 |
5/3 |
0 |
0 |
Проверим полученный базисный план на оптимальность по условию оптимальности: В симплекс-таблице в столбце базисных переменных нет отрицательных элементов, значит данное базисное решение оптимально.
Значение целевой функции не изменилось по сравнению с исходным оптимальным решением. С помощью графического способа можно убедиться, что оптимальное решение не принадлежит прямой, являющейся дополнительным ограничением, следовательно, дополнительное ограничение НЕАКТИВНОЕ.
3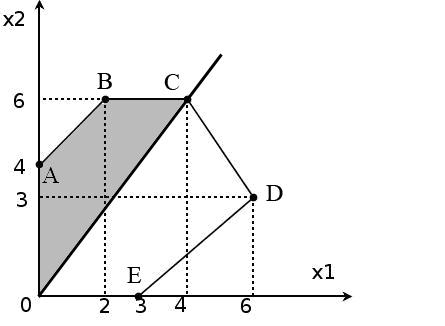 )
Введем дополнительное ограничение:
)
Введем дополнительное ограничение:
Уравнение прямой имеет вид:
6x1-4x2=0
Ограничение имеет вид:
6x1-4x2<=0
Представим в канонической форме:
6x1-4x2+x7=0
Выразим x2: x2=6-x4.
Выразим x1: x1=4+2/3x4-1/3x5
Формируем новую строку симплекс таблицы:
8x4-2x5+x7=0
|
Базис |
B |
|
|
|
|
|
|
|
|
|
6 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
|
4 |
1 |
0 |
0 |
-2/3 |
1/3 |
0 |
0 |
|
|
2 |
0 |
0 |
1 |
-5/3 |
1/3 |
0 |
0 |
|
|
5 |
0 |
0 |
0 |
5/3 |
-1/3 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
8 |
-2 |
0 |
1 |
|
|
62 |
0 |
0 |
0 |
11/3 |
5/3 |
0 |
0 |
Проверим полученный базисный план на оптимальность по условию оптимальности: В симплекс-таблице в столбце базисных переменных нет отрицательных элементов, значит данное базисное решение оптимально.
Значение целевой функции не изменилось по сравнению с исходным оптимальным решением. С помощью графического способа можно убедиться, что оптимальное решение лежит на прямой, являющейся дополнительным ограничением, следовательно, дополнительное ограничение ИЗБЫТОЧНОЕ.
