
Липецкий государственный технический университет
Кафедра автоматизированных систем управления
ЛАБОРАТОРНАЯ РАБОТА №8
по Теории принятия решений
Транспортная задача (часть 2)
|
|
Студент |
|
|
|
Ключанских А.С |
|
||||||||
|
|
|
|
подпись, дата |
|
фамилия, инициалы |
|
||||||||
|
|
Группа |
|
АС-10 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
Принял |
|
|
|
|
|
||||||||
|
|
доцент |
|
|
|
Корнеев А.М. |
|
||||||||
|
|
ученая степень, звание |
|
подпись, дата |
|
фамилия, инициалы |
|
||||||||
Липецк 2013
1. Задание
Решить транспортную задачу:
1. Методом дифференциальных рент.
2. Венгерским методом.
2. Решение
|
Вариант 10 |
Потребители (B) |
|||||
|
111 |
120 |
118 |
115 |
121 |
||
|
Производители (A) |
113 |
8 |
4 |
6 |
3 |
10 |
|
117 |
4 |
5 |
3 |
7 |
10 |
|
|
120 |
6 |
9 |
5 |
3 |
7 |
|
|
235 |
9 |
11 |
6 |
4 |
9 |
|
-
Решим транспортную задачу методом дифференциальных рент.
Итерация 1

В каждом столбце таблицы находим минимальные тарифы, закрашиваем их серым цветом, а соответствующие им клетки заполняем по следующему правилу: сначала заполняются те строки и столбцы, в которых выделена серым только одна клетка, после чего соответствующая строка\столбец исключается из рассмотрения. Затем находим избыточные и недостаточные строки и записываем справа от строки соответствующее число:
Строка 1: 113-113-7=-7 (т.к. все запасы первого поставщика исчерпаны, и при этом второму потребителю не хватило 7 единиц).
Строка 2: 117-111-6-112=-112 (третьему потребителю не хватило 112 единиц)
Строка 3: 120-115-5-116=-116.
Строка 4: 235-0=235.
Далее находим разности по столбцам между тарифами, выделенными серым цветом и ближайшим к ним минимальным тарифом, расположенным в избыточной строке, при условии, что выделенный серым тариф расположен в недостаточной строке:
Столбец 1: 9-4=5
Столбец 2: 11-4=7
Столбец 3: 6-3=3
Столбец 4: 4-3=1
Столбец 5: 9-7=2
Находим среди этих разностей минимум, это число является промежуточной рентой. В данном случае она равна 1. Заполним новую таблицу, добавив промежуточную ренту ко всем тарифам в недостаточных строках и далее выполним все действия сначала по аналогии с первой итерацией.
Итерация 2

Итерация 3

Итерация 4

Итерация 5
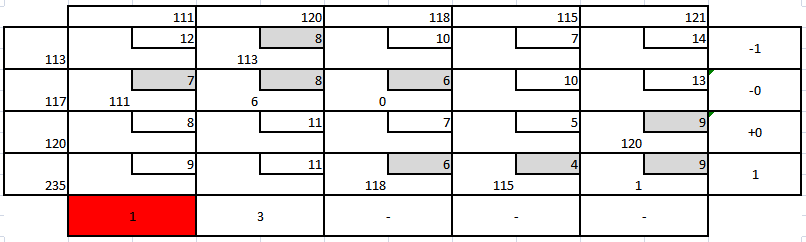
Итерация 6

Нераспределенный остаток равен нулю, следовательно, процесс вычислений прекращается. Транспортные расходы: f = 2952.
-
Решим данную задачу Венгерским методом.
Предварительный этап

![]()
Х0=
![]()
![]()
![]()
![]()
Итерация 1
Первый этап
Выделяем знаком + те столбцы матрицы С0, в которых невязка по столбцам равна 0. В данном случае это столбцы 1 и 4.
![]()

![]()
Ищем нули в невыделенных столбцах, первый найденный такой нуль расположен в 1 строке во 2 столбце. Невязка по 1 строке равна 0, следовательно, помечаем данную строку знаком + справа от нее, а сам нуль – штрихом. Далее ищем в первой строке нули, которые находятся в выделенных столбцах и ищем среди них существенные нули. В данном случае есть нуль в 4 столбце, но существенным он не является, поэтому ищем следующий невыделенный нуль. Такой нуль имеется, он расположен во 2 строке 3 столбца. Проверяем невязку второй строки, она равна 0, отмечаем ее справа знаком +, а сам нуль – штрихом. Ищем существенные нули во 2 строке, которые расположены в выделенных столбцах. Такой нуль имеется, он находится в 1 столбце. Снимаем выделение с 1 столбца, отмечаем данный нуль знаком *, и просматриваем первый столбец на наличие нулей. Они отсутствуют. Далее ищем следующий невыделенный нуль, он находится в 3 строке 5 столбца. Невязка 3 строки равна нулю, отмечаем данную строку знаком + справа от нее, а сам нуль – штрихом. Ищем существенные нули в 3 строке в выделенных столбцах. Такой нуль имеется, в 4 столбце. Снимаем знак выделения со столбца, а сам нуль помечаем знаком * и просматриваем 4 столбец на наличие нулей. Нуль имеется в 4 строке 4 столбца, невязка 4 строки равна 235>0, поэтому отмечаем данный нуль штрихом и переходим ко второму этапу.
