МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА АВТОМАТИЗИРОВАННЫХ СИСТЕМ УПРАВЛЕНИЯ

Практическая работа №6

«Модифицированный симплекс-метод»

по дисциплине

«Теория принятия решений»

Студент

Филатов А.А.

подпись, дата

фамилия, инициалы

Группа

АС-09

Принял

Корнеев А.М.

ученая степень, звание

подпись, дата

фамилия, инициалы

Липецк 2012

1. Задание

1. Решить задачу линейного программирования, используя итерации модифицированного симплекс-метода.

2. Вычислить коэффициенты z-строки и определить включаемую в базис переменную .

3. Определить исключаемую переменную

4. Определить новый базис и перейти к шагу 2.

2. Решение

Целевая функция имеет вид: .

А область ограничений задачи в стандартной форме имеет вид:

Найденное оптимальное решение в предыдущих практических работах:

.

Начальное решение:

Итерация 1

Шаг 1 – Вычисление для небазисных векторов и .

Следовательно, включению в базис подлежит вектор .

Шаг 2 – Определение исключаемого вектора при введении в базис вектора .

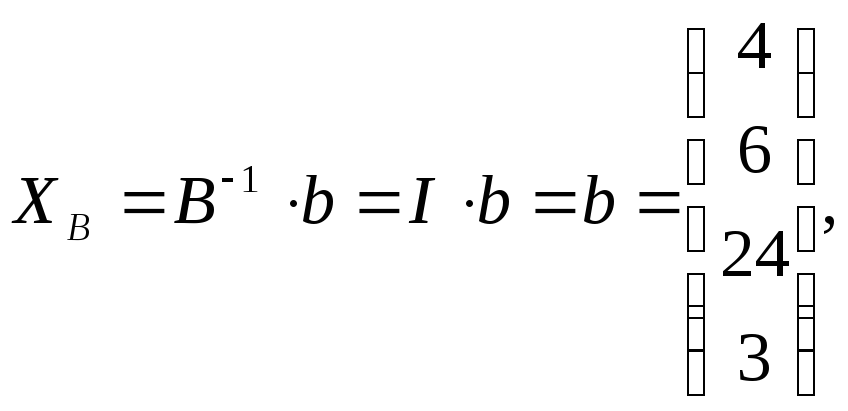
Базис							Решение
	-5	-7	0	0	0	0
		1					4
		1					6
		2					24
		-1					3

Отсюда следует, что

Значит, исключению из базиса подлежит вектор .

Шаг 3 – Определение обратной матрицы, соответствующей новому базису.

Так как вместо вектора в базис вводится вектор , то:

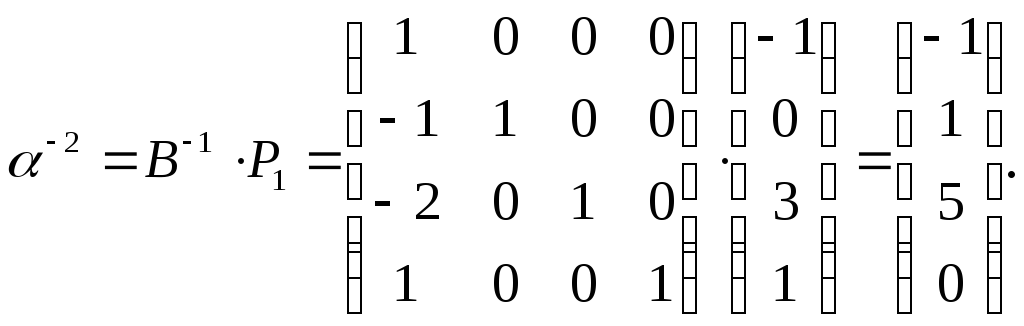
Новому базису соответствуют векторы:

Итерация 2

Шаг 1 – Вычисление для небазисных векторов и .

Следовательно, включению в базис подлежит вектор .

Шаг 2 – Определение исключаемого вектора при введении в базис вектора .

Базис							Решение
	-12	0	7	0	0	0
	-1						4
	1						2
	5						16
	1						7

Отсюда следует, что

Значит, исключению из базиса подлежит вектор .

Шаг 3 – Определение обратной матрицы, соответствующей новому базису.

Так как вместо вектора в базис вводится вектор , то:

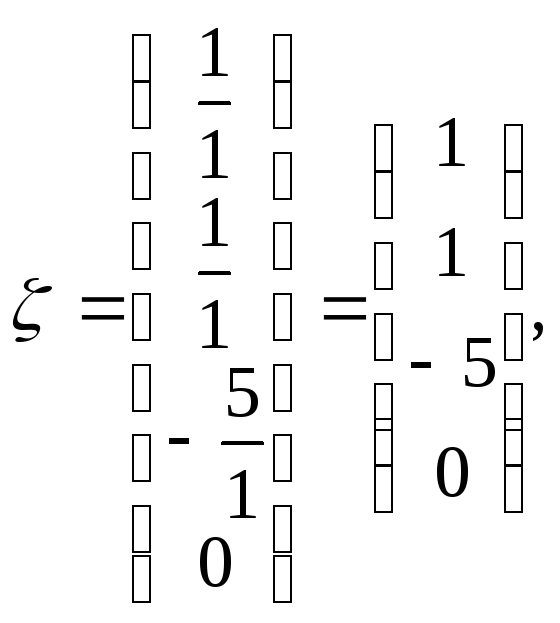
Новому базису соответствуют векторы:

Итерация 3

Шаг 1 – Вычисление для небазисных векторов и .

Следовательно, включению в базис подлежит вектор .

Шаг 2 – Определение исключаемого вектора при введении в базис вектора .

Базис							Решение
	0	0	-5	12	0	0
			0				6
			-1				2
			3				6
			1				7

Отсюда следует, что

Значит, исключению из базиса подлежит вектор .

Шаг 3 – Определение обратной матрицы, соответствующей новому базису.

Так как вместо вектора в базис вводится вектор , то:

Новому базису соответствуют векторы:

Итерация 4

Шаг 1 – Вычисление для небазисных векторов и .

Так как для всех , то полученный базис соответствует оптимальному решению.

Полученное оптимальное решение