3.2.4 Апериодическое (инерционное, статическое) звено первого порядка

Д ифференциальное уравнение апериодического звена первого порядка имеет вид

а операторная форма записи – изображение этого уравнения

И з этого выражения можно получить передаточную функцию

Примером ПФ апериодического звена может служить фильтр низкой частоты на RC или RL элементах.

После необходимых преобразований получим

Изменяя частоту ω от 0 до ∞, можно построить годограф (рис.3.4), представляющий собой полуокружность, расположенную в четвертом квадранте комплексной плоскости, диаметр которой равен коэффициенту k.

Рисунок 3.4 – Частотные и временные характеристики апериодического звена 1 порядка

В ЛАЧХ амплитуда ПФ остается постоянной и равной 20lgk до частоты ω₁ = 1/Т называемой сопрягаемой частотой, после нее происходит уменьшение амплитуды через каждую декаду на 20 децибел (-20 дб/дек). Частота, при которой амплитуда ПФ равна единицы, называется частотой среза ω_с А(ω_с) = 1, после которой система теряет усилительные свойства A(ω) < 1.

Кривая разгона апериодического звена имеет форму экспоненты. Если к любой ее точке провести касательную, а затем точку касания и точку пересечения касательной с асимптотой, спроецировать на ось времени, то получится один и тот же отрезок на оси времени. Эта проекция, называемая постоянной времени, соответствует коэффициенту Т в передаточной функции.

Таким образом по кривой разгона легко найти коэффициента k и Т в передаточной функции апериодического звена. Примером реализации апериодического звена является электродвигатель небольшой мощности, который после включения в электросеть (подачи единичного скачка) набирает обороты по экспоненте. Объекты с передаточной функцией апериодического звена называют статическими.

3.2.5 Форсирующее звено 1 порядка

При моделировании систем приходится сталкиваться со звеньями, которые не входят в разряд типовых, но которые оказывают отрицательное влияние на устойчивость. К ним относятся форсирующие 1 и 2 порядков, консервативное и неминимально-фазовые звенья.

Форсирующее звено 1 порядка напоминает апериодическое звено 1 порядка, но ПФ и частотные свойства противоположные.

W(p) = k (Tp +1).

Для построения годографа поставим в ПФ p = jω и получим

W(jω) = k (1 + jTω).

Изменяя частоту ω от 0 до ∞, строится годограф (рисунок 3.5), представляющий собой прямую параллельную мнимой положительной полуоси и расположенную во втором квадранте комплексной плоскости.

Рисунок 3.5 – Частотные характеристики форсирующего звена 1 порядка

Как видно их частотных характеристик после сопрягаемой частоты ω₁ = 1/Т амплитуда ПФ резко возрастает и звено (система) становится неустойчивой, т.е. такие звенья применять в структурной схеме нежелательно.

3.2.6 Апериодическое звено 2-го порядка

Д ифференциальное уравнение этого звена имеет вид

В операторной форме записи (Т₁р² + Т₂ р + 1) у (р) = k х(р)

или

где

П ередаточная функция имеет вид

Существуют три вида апериодических звеньев 2 порядка в зависимости от величины коэффициента демпфирования ξ :

а) ξ ≥ 1 – апериодическое звено 2 порядка;

б) 0 < ξ < 1 – колебательное звено;

в) ξ = 0 – консервативное звено.

А. Апериодическое звено 2 порядка (ξ ≥ 1)

ПФ звена преобразуется как два последовательно соединенных апериодических звена 1 порядка.

где

Таким образом, апериодическое звено 2 порядка при ξ ≥ 1 ведет себя также как и 2 апериодических звена 1 порядка. Поэтому АФЧХ и ФЧХ аналогичны звену первого порядка, но с наклоном ЛАЧХ при ω₁ = 1/Т₁ -20 дб/дек и затем при ω₂ = 1/Т₂ еще раз -20дб/дек. Общий наклон составит - 40дб/дек.

Б. Колебательное звено (0 < ξ < 1)

Подставив р = jω в ПФ звена, получим

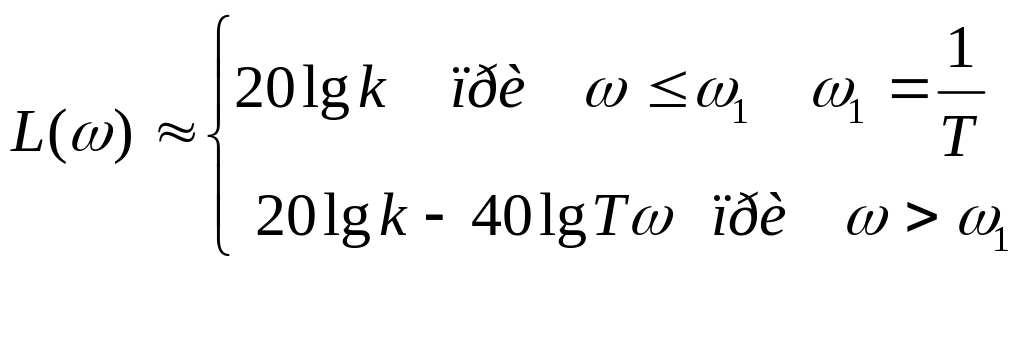
Фазо-частотная характеристика звена имеет следующие значения

Решив дифференциальное уравнения звена при х(t) =1 при нулевых начальных условиях, получим переходную функцию h(t) или кривую разгона

где (3.1)

Рисунок 3.6 – Частотные и временные характеристики колебательного звена

По кривой разгона можно вычислить постоянную времени Т и ξ колебательного звена. Измерив период колебаний Т_к и амплитуды колебаний А₁ и А₂ на кривой разгона, находят коэффициенты α и β по формулам

Подставив рассчитанные значения коэффициентов α и β в (3.1) и решая систему уравнений с двумя неизвестными, определяются Т и ξ.

Объекты, описываемые колебательным звеном, обладают свойством самовыравнивания, т.е. способностью самостоятельно восстанавливать состояние равновесия после возмущающего воздействия.

В. Консервативное звено (ξ = 0)

ПФ звена равна

Фаза ПФ звена при различных значениях частоты имеет вид

Рисунок 3.7 – Частотные и временные характеристики консервативного звена

Как видно из ЛАЧХ при сопрягаемой частоте амплитуда ПФ стремится к бесконечности, т.е. происходит явление резонанса. Переходная характеристика убеждает в нежелательности применения этого звена, т.к. при подаче единичного воздействия возникают незатухающие колебания.